With this material on power series, it becomes possible to give an understandable treatment of the exponential function exp and the circular functions, sin and cos. A definition could be given directly for $x \in \mathbb{C}$ but in this section, it is assumed $x \in \mathbb{R}$.
8.3.1 Sines and Cosines
To begin with here is a definition of $\sin , \cos$, and exp.
Definition 8.3.1 Define for all $x \in \mathbb{R}$
$$
\sin (x) \equiv \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k+1}}{(2 k+1) !}, \cos (x) \equiv \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}, \exp (x) \equiv \sum_{k=0}^{\infty} \frac{x^{k}}{k !} .
$$
Observation 8.3.2 The above series converge for all $x \in \mathbb{F}$. This is most easily seen using the ratio test. Consider the series for $\sin (x)$ first. By the ratio test the series converges whenever
$$
\lim {k \rightarrow \infty} \frac{\frac{|x|^{2 k+3}}{(2 k+3) !}}{\frac{|x|^{2 k+1}}{(2 k+1) !}}=\lim {k \rightarrow \infty} \frac{1}{(2 k+3)(2 k+1)}|x|^{2}
$$
is less than 1. However, this limit equals o for any $x$ and so the series converges for all $x$. The verification of convergence for the other two series is left for you to do and is no harder. In what follows, I will emphasize $x$ real. To do it for arbitrary $x \in \mathbb{C}$ is really a topic for complex analysis.
Now that $\sin (x)$ and $\cos (x)$ have been defined, the properties of these functions must be considered. First, here is a fundamental lemma.
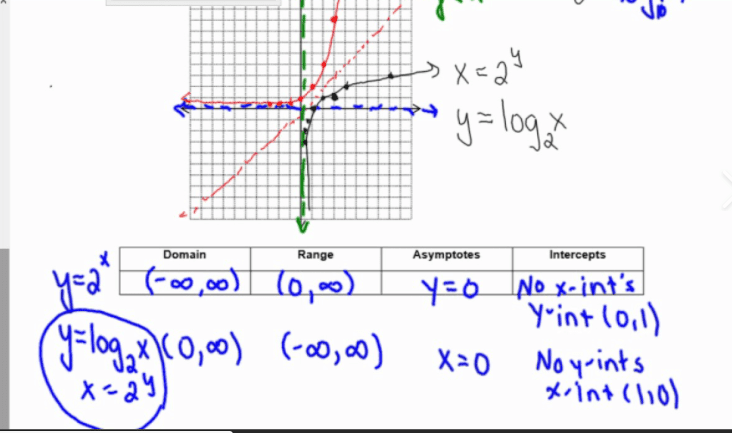
希望能够区分和乘幂级数。记起
$$
f^{\prime}(x) \equiv \lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}
$$
这里 $h, x, f$ 都可以有 $\mathbb{C}$ 中的值。下面的定理说你可以在收敛盘上以最自然的方式微分幂级数,就像你微分多项式一样。这个定理似乎很明显,但这样想是一个严重的错误。即使函数本身是多项式,您通常也无法区分其项是函数的无限级数。以下是特殊的,属于幂级数。这是两个极限互换的另一个例子,在这种情况下,取导数所涉及的极限和有限和序列的极限。
当您正式区分一个系列术语时,结果称为派生系列。
定理 8.2.1 令 $\sum_{n=0}^{\infty} a_{n}(x-a)^{n}$ 是一个泰勒级数,其收敛半径为 $R>0$,并令
$$
f(x) \equiv \sum_{n=0}^{\infty} a_{n}(x-a)^{n}
$$
对于 $|x-a|<R$。然后
$$
f^{\prime}(x)=\sum_{n=0}^{\infty} a_{n} n(xa)^{n-1}=\sum_{n=1}^{\infty} a_ {n} n(xa)^{n-1}
$$
而这个新的微分幂级数,即派生级数,其收敛半径等于 R。此外,泰勒级数给出的 $f(x)$ 在其收敛圆盘的内部是无限可微的。
证明:首先考虑派生级数的收敛半径等于$R$。令 $\hat{R}$ 为派生级数的收敛半径。然后来自命题 $4.10 .13$ 和引理 8.1.2。
$$
\frac{1}{\hat{R}} \equiv \lim \sup {n \rightarrow \infty}\left|a{n}\right|^{1 / n} n^{1 / n}= \lim \sup {n \rightarrow \infty}\left|a{n}\right|^{1 / n} \equiv \frac{1}{R}
$$
所以$\hat{R}=R$。如果$\limsup {n \rightarrow \infty}\left|a{n}\right|^{1 / n}=0$,同样适用于$\limsup_{n \rightarrow \infty}\left |a_{n}\right|^{1 / n} n^{1 / n}$ 并且在这种情况下,级数和派生级数的收敛半径都等于 $\infty$。
现在让$r<R$,两个级数的收敛半径,假设$|x-a|<r$。令 $\delta$ 足够小,如果 $|h|<\delta$,那么
$$
|x+h-a| \leq|x-a|+|h|<r
$$
还。因此,$\lim \sup_{k \rightarrow \infty}\left|a_{k}\right|^{1 / k} r<1$。
然后对于 $|h|<\delta$,考虑差商。
$$
\frac{f(x+h)-f(x)}{h}=\frac{1}{h} \sum_{k=0}^{\infty} a_{k}\left((x+ha )^{k}-(xa)^{k}\right)
$$使用二项式定理,
$$
\开始{对齐}
\frac{f(x+h)-f(x)}{h} &=\frac{1}{h} \sum_{k=0}^{\infty} a_{k}\left((x+ ha)^{k}-(xa)^{k}\right) \
&=\frac{1}{h} \sum_{k=1}^{\infty} a_{k}\left(\sum_{j=0}^{k}\left(\begin{array}{c }
k \
j
\end{数组}\right)(x-a)^{j} h^{k-j}-(x-a)^{k}\right) \
&=\sum_{k=1}^{\infty} a_{k}\left(\sum_{j=0}^{k-1}\left(\begin{array}{c}
k \
j
\end{数组}\right)(x-a)^{j} h^{(k-1)-j}\right)
\end{对齐}
$$
然后
$$
\开始{对齐}
&\left|\frac{f(x+h)-f(x)}{h}-\sum_{k=1}^{\infty} a_{k} k(xa)^{k-1}\对| \
=&\left|\sum_{k=1}^{\infty} a_{k}\left(\sum_{j=0}^{k-1}\left(\begin{array}{c}
k \
j
\end{数组}\right)(x-a)^{j} h^{(k-1)-j}-k(x-a)^{k-1}\right)\right| \
=&\left|\sum_{k=2}^{\infty} a_{k}\left(\sum_{j=0}^{k-1}\left(\begin{array}{c}
k \
j
\end{数组}\right)(x-a)^{j} h^{(k-1)-j}-k(x-a)^{k-1}\right)\right| \
=&\left|\sum_{k=2}^{\infty} a_{k}\left(\sum_{j=0}^{k-2}\left(\begin{array}{c}
k \
j
\end{数组}\right)(x-a)^{j} h^{(k-1)-j}\right)\right|
\end{对齐}
$$
所以,
$$
\left|\frac{f(x+h)-f(x)}{h}-\sum_{k=1}^{\infty} a_{k} k(xa)^{k-1}\right | \leq \sum_{k=2}^{\infty}\left|a_{k}\right|\left(\sum_{j=0}^{k-2}\left(\begin{array}{c }
k \
j
\end{数组}\right)|x-a|^{j}|h|^{(k-1)-j}\right)
$$
现在很清楚 $k(k-1)\left(\begin{array}{c}k-2 \ j\end{array}\right) \geq\left(\begin{array}{l} k \ j\end{array}\right)$ 等等
$$
\开始{对齐}
&=|h| \sum_{k=2}^{\infty}\left|a_{k}\right|\left(\sum_{j=0}^{k-2}\left(\begin{array}{c}
k \
j
\end{数组}\right)|x-a|^{j}|h|^{(k-2)-j}\right) \
&\leq|h| \sum_{k=2}^{\infty}\left|a_{k}\right| k(k-1) \sum_{j=0}^{k-2}\left(\begin{数组}{c}
k-2 \
j
\end{数组}\right)|x-a|^{j}|h|^{(k-2)-j}
\end{对齐}
$$
$=|h| \sum_{k=2}^{\infty}\left|a_{k}\right| k(k-1)(|x-a|+|h|)^{k-2}<|h| \sum_{k=2}^{\infty}\left|a_{k}\right| k(k-1)$ 假设和刚刚观察到的关于 $\lim {k \rightarrow \infty} k^{1 / k}$ 通过假设和刚刚观察到的关于 $\lim {k \rightarrow \infty} k^{1 / k}$, $$ \lim \sup {k \rightarrow \infty}\left(\left|a{ k}\right| k(k-1) r^{k-2}\right)^{1 / k}<1 $$
$$
\left|\frac{f(x+h)-f(x)}{h}-\sum_{k=1}^{\infty} a_{k} k(xa)^{k-1}\right |<C|h|
$$

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。