It is very important to be able to compare the size of sets in a rational way. The most useful theorem in this context is the Schroder Bernstein theorem which is the main result to be presented in this section. The Cartesian product is discussed above. The next definition reviews this and defines the abstract notion of a function.
Definition 3.2.1 Let $X$ and $Y$ be sets. $X \times Y \equiv{(x, y): x \in X$ and $y \in Y}$. A relation is defined to be a subset of $X \times Y$. A function $f$, also called a mapping, is a
CHAPTER 3. SET THEORY
42
relation which has the property that if $(x, y)$ and $\left(x, y_{1}\right)$ are both elements of the $f$, then $y=y_{1}$. The domain of $f$ is defined as
$$
D(f) \equiv{x:(x, y) \in f},
$$
written as $f: D(f) \rightarrow Y$ and we write $y=f(x)$. Another notation which is used is the following
$$
f^{-1}(y) \equiv{x \in D(f): f(x)=y}
$$
This is called the inverse image.
It is probably safe to say that most people do not think of functions as a type of relation which is a subset of the Cartesian product of two sets. A function is like a machine which takes inputs, $x$ and makes them into a unique output, $f(x)$. Of course, that is what the above definition says with more precision. An ordered pair, $(x, y)$ which is an element of the function or mapping has an input, $x$ and a unique output $y$, denoted as $f(x)$ while the name of the function is $f$. “mapping” is often a noun meaning function. However, it also is a verb as in ” $f$ is mapping $A$ to $B$ “. That which a function is thought of as doing is also referred to using the word “maps” as in: $f$ maps $X$ to $Y$. However, a set of functions may be called a set of maps so this word might also be used as the plural of a noun. There is no help for it. You just have to suffer with this nonsense.
The following theorem which is interesting for its own sake will be used to prove the Schroder Bernstein theorem, proved by Dedekind in 1887 . The shortest proof I have seen is in Hewitt and Stromberg [16] and this is the version given here. There is another version in Halmos [14].
$$
\begin{gathered}
A \cup B=X, C \cup D=Y, A \cap B=\emptyset, C \cap D=\emptyset, \
f(A)=C, g(D)=B .
\end{gathered}
$$
The following picture illustrates the conclusion of this theorem.
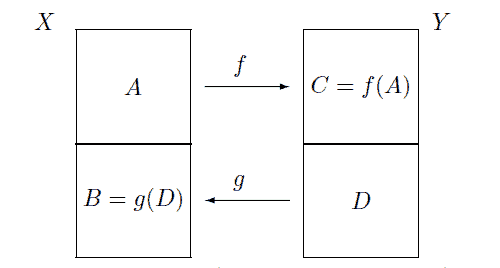
Proof: Consider the empty set, $\emptyset \subseteq X .$ If $y \in Y \backslash f(\emptyset)$, then $g(y) \notin \emptyset$ because $\emptyset$ has no elements. Also, if $A, B, C$, and $D$ are as described above, $A$ also would have this same property that the empty set has. However, $A$ is probably larger. Therefore, say $A_{0} \subseteq X$ satisfies $\mathcal{P}$ if whenever $y \in Y \backslash f\left(A_{0}\right), g(y) \notin A_{0}$.
$$
\mathcal{A} \equiv\left{A_{0} \subseteq X: A_{0} \text { satisfies } \mathcal{P}\right} .
$$
Let $A=\cup \mathcal{A}$. If $y \in Y \backslash f(A)$, then for each $A_{0} \in \mathcal{A}, y \in Y \backslash f\left(A_{0}\right)$ and so $g(y) \notin A_{0}$. Since $g(y) \notin A_{0}$ for all $A_{0} \in \mathcal{A}$, it follows $g(y) \notin A$. Hence $A$ satisfies $\mathcal{P}$ and is the largest subset of $X$ which does so. Now define
$$
C \equiv f(A), D \equiv Y \backslash C, B \equiv X \backslash A
$$
3.2. THE SCHRODER BERNSTEIN THEOREM
43
It only remains to verify that $g(D)=B$. It was just shown that $g(D) \subseteq B$.
Suppose $x \in B=X \backslash A$. Then $A \cup{x}$ does not satisfy $\mathcal{P}$ because it is too large, and so there exists $y \in Y \backslash f(A \cup{x}) \subseteq D$ such that $g(y) \in A \cup{x}$. But $y \notin f(A)$ and so since $A$ satisfies $\mathcal{P}$, it follows $g(y) \notin A$. Hence $g(y)=x$ and so $x \in g(D)$. Hence $g(D)=B$.
能够以合理的方式比较集合的大小是非常重要的。在这种情况下,最有用的定理是施罗德伯恩斯坦定理,这是本节要介绍的主要结果。笛卡尔积在上面讨论过。下一个定义对此进行了回顾并定义了函数的抽象概念。
定义 3.2.1 设 $X$ 和 $Y$ 为集合。 $X \times Y \equiv{(x, y): x \in X$ 和 $y \in Y}$。关系被定义为 $X\times Y$ 的子集。函数 $f$,也称为映射,是
第三章集合论
42
具有如下性质的关系:如果 $(x, y)$ 和 $\left(x, y_{1}\right)$ 都是 $f$ 的元素,则 $y=y_{1}$。 $f$ 的定义域为
$$
D(f) \equiv{x:(x, y) \in f},
$$
写成 $f: D(f) \rightarrow Y$ 我们写成 $y=f(x)$。使用的另一种表示法如下
$$
f^{-1}(y) \equiv{x \in D(f): f(x)=y}
$$
这称为反转图像。
可以肯定地说,大多数人并不认为函数是一种关系类型,它是两组笛卡尔积的子集。函数就像一台机器,它接受输入 $x$ 并将它们变成唯一的输出 $f(x)$。当然,这就是上面的定义更精确地表达的意思。一个有序对 $(x, y)$ 是函数或映射的一个元素,它有一个输入 $x$ 和一个唯一的输出 $y$,表示为 $f(x)$ 而函数的名称是$f$。 “映射”通常是名词意义功能。然而,它也是一个动词,如“$f$ is mapping $A$ to $B$”。函数被认为正在做的事情也可以使用“映射”一词来指代,如:$f$ 将 $X$ 映射到 $Y$。但是,一组函数可以称为一组映射,因此这个词也可以用作名词的复数形式。没有任何帮助。你只需要忍受这种胡说八道。
以下定理本身很有趣,将用于证明 Dedekind 在 1887 年证明的施罗德伯恩斯坦定理。我见过的最短证明是在 Hewitt 和 Stromberg [16] 中,这是这里给出的版本。 Halmos [14] 中还有另一个版本。
$$
\begin{equation}
A \cup B=X, C \cup D=Y, A \cap B=\emptyset, C \cap D=\emptyset, \
f(A)=C,g(D)=B。
\end{equation}
$$
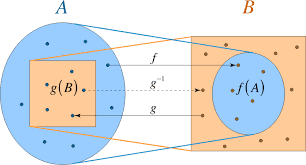
下图说明了这个定理的结论。
证明:考虑空集 $\emptyset \subseteq X .$ 如果 $y \in Y \backslash f(\emptyset)$,那么 $g(y) \notin \emptyset$ 因为 $\emptyset$ 没有元素。此外,如果 $A、B、C$ 和 $D$ 如上所述,则 $A$ 也将具有与空集相同的属性。但是,$A$ 可能更大。因此,假设 $A_{0} \subseteq X$ 满足 $\mathcal{P}$ 如果每当 $y \in Y \backslash f\left(A_{0}\right), g(y) \notin A_{0 }$。
$$
\mathcal{A} \equiv\left{A_{0} \subseteq X: A_{0} \text { 满足 } \mathcal{P}\right} 。
$$
令$A=\cup \mathcal{A}$。如果 $y \in Y \backslash f(A)$,那么对于每个 $A_{0} \in \mathcal{A},y \in Y \backslash f\left(A_{0}\right)$ 等等$g(y) \notin A_{0}$。由于 $g(y) \notin A_{0}$ 对于所有 $A_{0} \in \mathcal{A}$,它遵循 $g(y) \notin A$。因此 $A$ 满足 $\mathcal{P}$ 并且是 $X$ 的最大子集。现在定义
$$
C \equiv f(A), D \equiv Y \反斜杠 C, B \equiv X \反斜杠 A
$$
3.2.施罗德伯恩斯坦定理
43
只需验证$g(D)=B$。刚刚证明了 $g(D) \subseteq B$。
假设 $x \in B=X \反斜杠 A$。那么 $A \cup{x}$ 不满足 $\mathcal{P}$ 因为它太大了,所以存在 $y \in Y \backslash f(A \cup{x}) \子集 D$ 使得 $g(y) \in A \cup{x}$。但是 $y \notin f(A)$ 并且因为 $A$ 满足 $\mathcal{P}$,所以它遵循 $g(y) \notin A$。因此 $g(y)=x$ 等 $x \in g(D)$。因此$g(D)=B$。

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。