0 0

By admin 数学代写 2022年2月23日

7.8 Mean Value Theorem
The mean value theorem is possibly the most important theorem about the derivative of a function of one variable. It pertains only to a real valued function of a real variable. The best versions of many other theorems depend on this fundamental result. The mean value theorem is based on the following special case known as Rolle’s theorem². It is an existence theorem and like the other existence theorems in analysis, it depends on the completeness axiom.
Theorem 7.8.1 Suppose $f:[a, b] \rightarrow \mathbb{R}$ is continuous,
$$
f(a)=f(b),
$$
and
$$
f:(a, b) \rightarrow \mathbb{R}
$$
has a derivative at every point of $(a, b)$. Then there exists $x \in(a, b)$ such that $f^{\prime}(x)=$ 0 .

Proof: Suppose first that $f(x)=f(a)$ for all $x \in[a, b]$. Then any $x \in(a, b)$ is a point such that $f^{\prime}(x)=0$. If $f$ is not constant, either there exists $y \in(a, b)$ such that $f(y)>f(a)$ or there exists $y \in(a, b)$ such that $f(y)<f(b)$. In the first case, the maximum of $f$ is achieved at some $x \in(a, b)$ and in the second case, the minimum of $f$ is achieved at some $x \in(a, b)$. Either way, Theorem 7.6.2 implies $f^{\prime}(x)=0$.

The next theorem is known as the Cauchy mean value theorem. It is the best version of this important theorem.

Theorem 7.8.2 Suppose $f, g$ are continuous on $[a, b]$ and differentiable on $(a, b)$. Then there exists $x \in(a, b)$ such that
calculus. This may be because, until Bolzano and Cauchy and later Weierstrass, there were aspects of calculus which were fairly fuzzy. In particular, the notion of differential was not precise and yet it was being used. 142 $\frac{f^{\prime}(x)(g(b)-g(a))=g^{\prime}(x)(f(b)-f(a))}{\hline \text { 2 Rolle is remembered for Rolle’s theorem and not for anything else he did. Ironically, he did not like }}$
Proof: Let
$$
h(x) \equiv f(x)(g(b)-g(a))-g(x)(f(b)-f(a))
$$
Then letting $x=a$ and then letting $x=b$, a short computation shows $h(a)=h(b)$. Also, $h$ is continuous on $[a, b]$ and differentiable on $(a, b)$. Therefore Rolle’s theorem applies and there exists $x \in(a, b)$ such that
$$
h^{\prime}(x)=f^{\prime}(x)(g(b)-g(a))-g^{\prime}(x)(f(b)-f(a))=0 .
$$
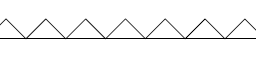
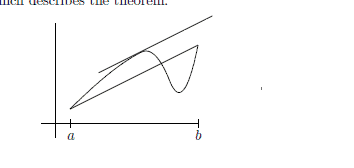
Letting $g(x)=x$, the usual version of the me
an value theorem is obtained. Here is the usual picture which
describes the theorem.‘
Corollary $7.8 .3$ Let $f$ be a continuous real valued function defined on $[a, b]$ and differentiable on $(a, b)$. Then there exists $x \in(a, b)$ such that $f(b)-f(a)=f^{\prime}(x)(b-a)$.
Corollary 7.8.4 Suppose $f^{\prime}(x)=0$ for all $x \in(a, b)$ where $a \geq-\infty$ and $b \leq \infty$. Then $f(x)=f(y)$ for all $x, y \in(a, b)$. Thus $f$ is a constant.

Proof: If this is not true, there exists $x_{1}$ and $x_{2}$ such that $f\left(x_{1}\right) \neq f\left(x_{2}\right)$. Then by the mean value theorem,
$$
0 \neq \frac{f\left(x_{1}\right)-f\left(x_{2}\right)}{x_{1}-x_{2}}=f^{\prime}(z)
$$
for some $z$ between $x_{1}$ and $x_{2}$. This contradicts the hypothesis that $f^{\prime}(x)=0$ for all $x$. This proves the theorem in the case that $f$ has real values. In the general case,
$$
f(x+h)-f(x)-0 h=o(h) .
$$
Then taking the real part of both sides,
$$
\operatorname{Re} f(x+h)-\operatorname{Re} f(x)=\operatorname{Re} o(h)=o(h)
$$
and so $\operatorname{Re} f^{\prime}(x)=0$ and by the first part, $\operatorname{Re} f$ must be a constant. The same reasoning applies to $\operatorname{Im} f$ and this proves the corollary.

Corollary 7.8.5 Suppose $f: \mathbb{C} \rightarrow \mathbb{C}$ and $f^{\prime}(x)=0$ for all $x$. Then $f$ is a constant.
Proof: Let $t \in \mathbb{R}$ and consider $h(t)=f(x+t(y-x))-f(x)$. Then by the chain rule,
$$
h^{\prime}(t)=f^{\prime}(x+t(y-x))(y-x)=0
$$
and so by Corollary 7.8.4, $h$ is a constant. In particular,
$$
h(1)=f(y)-f(x)=h(0)=0
$$
7.9. EXERCISES
143
Corollary 7.8.6 Suppose $f$ has real values and $f^{\prime}(x)>0$ for all $x \in(a, b)$ where $a \geq-\infty$ and $b \leq \infty$. Then $f$ is strictly increasing on $(a, b)$. That is, if $x<y$, then $f(x)<f(y) .$ If $f^{\prime}(x) \geq 0$, then $f$ is increasing in the sense that whenever $x<y$ it follows that $f(x) \leq f(y)$.

Proof: Let $xx$, it follows $f(y)>f(x)$ as claimed. Replacing $<$ by $\leq$ in the above equation and repeating the argument gives the second claim.

Corollary 7.8.7 Suppose $f^{\prime}(x)<0$ for all $x \in(a, b)$ where $a \geq-\infty$ and $b \leq \infty$. Then $f$ is strictly decreasing on $(a, b)$. That is, if $xf(y)$. If $f^{\prime}(x) \leq 0$, then $f$ is decreasing in the sense that for $x<y$, it follows that $f(x) \geq f(y)$

Proof: Let $xf^{\prime}(z)=\frac{f(y)-f(x)}{y-x} .
$$
Since $y>x$, it follows $f(y)<f(x)$ as claimed. The second claim is similar except instead of a strict inequality in the above formula, you put $\geq$.

7.8 中值定理
中值定理可能是关于一个变量的函数的导数的最重要的定理。它仅适用于实变量的实值函数。许多其他定理的最佳版本取决于这个基本结果。平均值定理基于以下称为罗尔定理²的特殊情况。它是一个存在定理，与分析中的其他存在定理一样，它依赖于完备性公理。
定理 7.8.1 假设 $f:[a, b] \rightarrow \mathbb{R}$ 是连续的，
$$
f(a)=f(b)，
$$
和
$$
f:(a, b) \rightarrow \mathbb{R}
$$
在 $(a, b)$ 的每一点都有一个导数。那么存在 $x \in(a, b)$ 使得 $f^{\prime}(x)=$ 0 。

证明：首先假设对于所有 $x \in[a, b]$，$f(x)=f(a)$。那么任何$x \in(a, b)$ 是一个满足$f^{\prime}(x)=0$ 的点。如果 $f$ 不是常数，要么存在 $y \in(a, b)$ 使得 $f(y)>f(a)$ 要么存在 $y \in(a, b)$ 使得 $ f(y)<f(b)$。在第一种情况下，$f$ 的最大值出现在某个 $x \in(a, b)$ 处，而在第二种情况下，$f$ 的最小值出现在某个 $x \in(a, b) 处美元。无论哪种方式，定理 7.6.2 都意味着 $f^{\prime}(x)=0$。

下一个定理被称为柯西中值定理。这是这个重要定理的最佳版本。

定理 7.8.2 假设 $f, g$ 在 $[a, b]$ 上连续且在 $(a, b)$ 上可微。那么存在 $x \in(a, b)$ 使得
结石。这可能是因为在博尔扎诺和柯西以及后来的魏尔斯特拉斯之前，微积分的某些方面是相当模糊的。特别是，微分的概念并不精确，但仍在使用。 142 $\frac{f^{\prime}(x)(g(b)-g(a))=g^{\prime}(x)(f(b)-f(a))}{\hline \text { 2 罗尔因罗尔定理而被人们记住，而不是因为他所做的任何其他事情。具有讽刺意味的是，他不喜欢 }}$
证明：让
$$
h(x) \equiv f(x)(g(b)-g(a))-g(x)(f(b)-f(a))
$$
然后让$x=a$，然后让$x=b$，一个简短的计算表明$h(a)=h(b)$。此外，$h$ 在 $[a, b]$ 上是连续的，并且在 $(a, b)$ 上是可微的。因此，罗尔定理适用并且存在 $x \in(a, b)$ 使得
$$
h^{\prime}(x)=f^{\prime}(x)(g(b)-g(a))-g^{\prime}(x)(f(b)-f(a) )=0 。
$$
让 $g(x)=x$，通常版本的 me
得到一个值定理。这是通常的图片
描述了这个定理。
推论 $7.8 .3$ 令 $f$ 是定义在 $[a, b]$ 上且在 $(a, b)$ 上可微的连续实值函数。那么存在$x \in(a, b)$ 使得$f(b)-f(a)=f^{\prime}(x)(b-a)$。
推论 7.8.4 假设所有 $x \in(a, b)$ 的 $f^{\prime}(x)=0$，其中 $a \geq-\infty$ 和 $b \leq \infty$。那么对于所有的 $x, y \in(a, b)$，$f(x)=f(y)$。因此$f$ 是一个常数。

证明：如果不成立，则存在 $x_{1}$ 和 $x_{2}$ 使得 $f\left(x_{1}\right) \neq f\left(x_{2}\right)美元。然后由中值定理，
$$
0 \neq \frac{f\left(x_{1}\right)-f\left(x_{2}\right)}{x_{1}-x_{2}}=f^{\prime}(z )
$$
$x_{1}$ 和 $x_{2}$ 之间的一些 $z$。这与所有 $x$ 的 $f^{\prime}(x)=0$ 的假设相矛盾。这证明了 $f$ 具有实值的情况下的定理。在一般情况下，
$$
f(x+h)-f(x)-0 h=o(h) 。
$$
然后取双方的实部，
$$
\operatorname{Re} f(x+h)-\operatorname{Re} f(x)=\operatorname{Re} o(h)=o(h)
$$
所以 $\operatorname{Re} f^{\prime}(x)=0$ 和第一部分，$\operatorname{Re} f$ 必须是一个常数。相同的推理适用于 $\operatorname{Im} f$，这证明了推论。

推论 7.8.5 假设对于所有的 $x$，$f: \mathbb{C} \rightarrow \mathbb{C}$ 和 $f^{\prime}(x)=0$。那么 $f$ 是一个常数。
证明：设$t \in \mathbb{R}$ 并考虑$h(t)=f(x+t(y-x))-f(x)$。然后通过链式法则，
$$
h^{\prime}(t)=f^{\prime}(x+t(y-x))(y-x)=0
$$
因此根据推论 7.8.4，$h$ 是一个常数。特别是，
$$
h(1)=f(y)-f(x)=h(0)=0
$$
7.9。练习
143
推论 7.8.6 假设 $f$ 有实数值并且对于所有 $x \in(a, b)$ 都有 $f^{\prime}(x)>0$ 其中 $a \geq-\infty$ 和 $b \莱克 \infty$。然后 $f$ 在 $(a, b)$ 上严格递增。也就是说，如果 $x<y$，那么 $f(x)<f(y) .$ 如果 $f^{\prime}(x) \geq 0$，那么 $f$ 在任何时候都在增加$x<y$ 它遵循 $f(x) \leq f(y)$。

证明：令 $xx$，它遵循 $f(y)>f(x)$ 的声明。将上述等式中的 $<$ 替换为 $\leq$ 并重复该参数给出了第二个声明。

推论 7.8.7 假设所有 $x \in(a, b)$ 的 $f^{\prime}(x)<0$ 其中 $a \geq-\infty$ 和 $b \leq \infty$。那么 $f$ 在 $(a, b)$ 上严格递减。也就是说，如果$xf(y)$。如果$f^{\prime}(x) \leq 0$，那么$f$ 是递减的，因为对于$x<y$，它遵循$f(x) \geq f(y)$

证明：令 $xf^{\prime}(z)=\frac{f(y)-f(x)}{y-x} 。
$$
由于 $y>x$，它遵循 $f(y)<f(x)$ 所声称的。第二个声明是相似的，只是在 abo 中没有严格的不等式