0 0

By admin 数学代写 2022年2月23日

9.5 Uniform Convergence and the Integral
It turns out that uniform convergence is very agreeable in terms of the integral. T following is the main result.

Theorem 9.5.1 Let $g$ be of bounded variation and let $f_{n}$ be continuous converging uniformly to $f$ on $[a, b]$. Then it follows $f$ is also integrable and
$$
\int_{a}^{b} f d g=\lim {n \rightarrow \infty} \int{a}^{b} f_{n} d g
$$
9.6. A SIMPLE PROCEDURE FOR FINDING INTEGRALS
Proof: The uniform convergence implies $f$ is also continuous. See Theorem $6.9$ Therefore, $\int_{a}^{b} f d g$ exists. Now let $n$ be given large enough that
$$
\left|f-f_{n}\right| \equiv \max {x \in[a, b]}\left|f(x)-f{n}(x)\right|<\varepsilon $$

Next pick $\delta>0$ small enough that if $|P|<\delta$, then
$$
\begin{aligned}
\left|\int_{a}^{b} f d g-\sum_{k=1}^{n} f\left(t_{k}\right)\left(g\left(x_{k}\right)-g\left(x_{k-1}\right)\right)\right| &<\varepsilon \
\left|\int_{a}^{b} f_{n} d g-\sum_{k=1}^{n} f_{n}\left(t_{k}\right)\left(g\left(x_{k}\right)-g\left(x_{k-1}\right)\right)\right| &<\varepsilon
\end{aligned}
$$
for any choice $t_{k} \in\left[x_{k-1}, x_{k}\right]$. Pick such a $P$ and the same $t_{k}$ for both sums. Then
$$
\begin{aligned}
\left|\int_{a}^{b} f d g-\int_{a}^{b} f_{n} d g\right| \leq &\left|\int_{a}^{b} f d g-\sum_{k=1}^{n} f\left(t_{k}\right)\left(g\left(x_{k}\right)-g\left(x_{k-1}\right)\right)\right| \
&+\left|\sum_{k=1}^{n}\left(f\left(t_{k}\right)-f_{n}\left(t_{k}\right)\right)\left(g\left(x_{k}\right)-g\left(x_{k-1}\right)\right)\right| \
&+\left|\int_{a}^{b} f_{n} d g-\sum_{k=1}^{n} f_{n}\left(t_{k}\right)\left(g\left(x_{k}\right)-g\left(x_{k-1}\right)\right)\right| \
<\varepsilon+\sum_{k=1}^{n} \varepsilon\left|g\left(x_{k}\right)-g\left(x_{k-1}\right)\right|+\varepsilon \leq 2 \varepsilon+V_{[a, b]}(g) \varepsilon
\end{aligned}
$$
Since $\varepsilon$ is arbitrary, this shows that $\lim {n \rightarrow \infty}\left|\int{a}^{b} f d g-\int_{a}^{b} f_{n} d g\right|=0$.

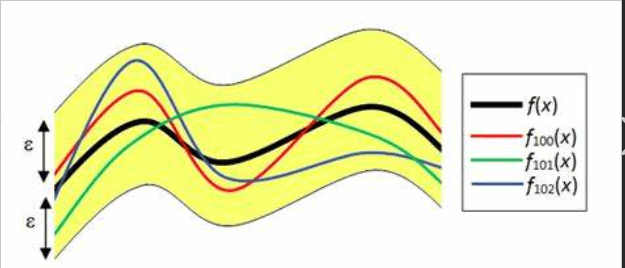
微积分note Uniform Convergence and the Integral 一致收敛

.5 一致收敛和积分
事实证明，一致收敛在积分方面是非常令人满意的。以下是主要结果。
定理 9.5.1 令 $g$ 有界变化，令 $f_{n}$ 在 $[a, b]$ 上连续一致地收敛到 $f$。然后它遵循 $f$ 也是可积的并且
$$
\int_{a}^{b} f d g=\lim {n \rightarrow \infty} \int{a}^{b} f_{n} d g
$$
9.6。寻找积分的简单程序
证明：一致收敛意味着$f$也是连续的。见定理 $6.9$ 因此，$\int_{a}^{b} f d g$ 存在。现在让 $n$ 足够大
$$
\left|f-f_{n}\right| \equiv \max {x \in[a, b]}\left|f(x)-f{n}(x)\right|<\varepsilon $$ 接下来选择足够小的$\delta>0$，如果$|P|<\delta$，那么
$$
\开始{对齐}
\left|\int_{a}^{b} fd g-\sum_{k=1}^{n} f\left(t_{k}\right)\left(g\left(x_{k}\right )-g\left(x_{k-1}\right)\right)\right| &<\伐普西隆 \
\left|\int_{a}^{b} f_{n} d g-\sum_{k=1}^{n} f_{n}\left(t_{k}\right)\left(g\left (x_{k}\right)-g\left(x_{k-1}\right)\right)\right| &<\伐普西隆
\end{对齐}
$$
对于任何选择 $t_{k} \in\left[x_{k-1}, x_{k}\right]$。为两个总和选择这样的 $P$ 和相同的 $t_{k}$。然后
$$
\开始{对齐}
\left|\int_{a}^{b} f d g-\int_{a}^{b} f_{n} d g\right| \leq &\left|\int_{a}^{b} fd g-\sum_{k=1}^{n} f\left(t_{k}\right)\left(g\left(x_{k }\right)-g\left(x_{k-1}\right)\right)\right| \
&+\left|\sum_{k=1}^{n}\left(f\left(t_{k}\right)-f_{n}\left(t_{k}\right)\right)\left (g\left(x_{k}\right)-g\left(x_{k-1}\right)\right)\right| \
&+\left|\int_{a}^{b} f_{n} d g-\sum_{k=1}^{n} f_{n}\left(t_{k}\right)\left(g \left(x_{k}\right)-g\left(x_{k-1}\right)\right)\right| \
<\varepsilon+\sum_{k=1}^{n} \varepsilon\left|g\left(x_{k}\right)-g\left(x_{k-1}\right)\right|+\varepsilon \leq 2 \varepsilon+V_{[a, b]}(g) \varepsilon
\end{对齐}
$$
由于 $\varepsilon$ 是任意的，这表明 $\lim {n \rightarrow \infty}\left|\int{a}^{b} fd g-\int_{a}^{b} f_{n} dg\right|=0$。