微积分(Calculus),数学概念,是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法
my-assignmentexpert™ 微积分calculus作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微积分calculus作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分calculus作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微积分calculus代写服务。我们的专家在微积分calculus学 代写方面经验极为丰富,各种微积分calculus相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 单变量微积分
- 多变量微积分
- 傅里叶级数
- 黎曼积分
- ODE
- 微分学
Definition 2.3.7 Let $f$ be defined in an open interval $I$. Then, for $k \in \mathbb{N}$ with $k \geq 2$, $f$ is said to be $k$ times differentiable at $x_{0} \in I$ if $f^{(1)}(x), f^{(2)}(x), \ldots, f^{(k-1)}(x)$ are defined iteratively as
$$
f^{(j)}(x):=\left[f^{(j-1)}\right]^{\prime}(x), \quad j=1, \ldots, k-1
$$
154
2 Limit, Continuity and Differentiability of Functions
for $x$ in a neighbourhood of $x_{0}$ with $f^{(0)}(x)=f(x)$ and
$$
f^{(k)}\left(x_{0}\right):=\left[f^{(k-1)}\right]^{\prime}\left(x_{0}\right)
$$
exists. Then $f^{(k)}\left(x_{0}\right)$ is called the $k^{\text {th }}$-derivative of $f$ at $x_{0}$.
Note that $f^{(2)}\left(x_{0}\right)$ is the second derivative of $f$ at $x_{0}$. The $k^{\text {th }}$-derivative of $f$ is also denoted by
$$
\frac{d^{k} f}{d x^{k}}
$$
It is also customary to use the notation $D f$ for $f^{\prime}$ and $D^{k} f$ for $f^{(k)}$, so that it is $D^{k} f=D\left(D^{k-1} f\right) .$
Definition 2.3.8 The function $f$ is said to be infinitely differentiable at a point $x_{0} \in I$ if $f$ has $k^{\text {th }}$-derivative at $x_{0}$ for every $k \in \mathbb{N}$.
We may observe the following: If $\mathrm{f}$ is infinitely differentiable at a point $x_{0} \in I$, then for every $k \in \mathbb{N}$, $\mathrm{f}$ has $k^{\text {th }}$-derivative not only at $x_{0}$ but also at every point in some neighbourhood of $x_{0}$. Example 2.3.29 For $n \in \mathbb{N}$, let $f(x)=x^{n}, x \in \mathbb{R}$. Then we know that $f^{(1)}(x)=$ $f^{\prime}(x)=n x^{n-1}$. Hence, for $k \leq n$, we have $$ f^{(k)}(x)=n(n-1) \cdots(n-k+1) x^{n-k} $$ and $f^{(k)}(x)=0$ for $k>n$. Thus, $f$ is infinitely differentiable in $\mathbb{R}$. More generally, if $f$ is a polynomial, then $f$ is infinitely differentiable in $\mathbb{R}$.
Example 2.3.30 Let $f(x)=\sin x, x \in \mathbb{R}$. Then we have
$$
f^{(1)}(x)=\cos x, \quad f^{(2)}(x)=-\sin x, \quad f^{(3)}(x)=-\cos x, \quad f^{(4)}(x)=\sin x
$$
and more generally for any $k \in \mathbb{N}$,
$$
f^{(2 k-1)}(x)=(-1)^{k+1} \cos x, \quad f^{(2 k)}(x)=(-1)^{k} \sin x .
$$
Thus, $f$ is infinitely differentiable in $\mathbb{R}$.
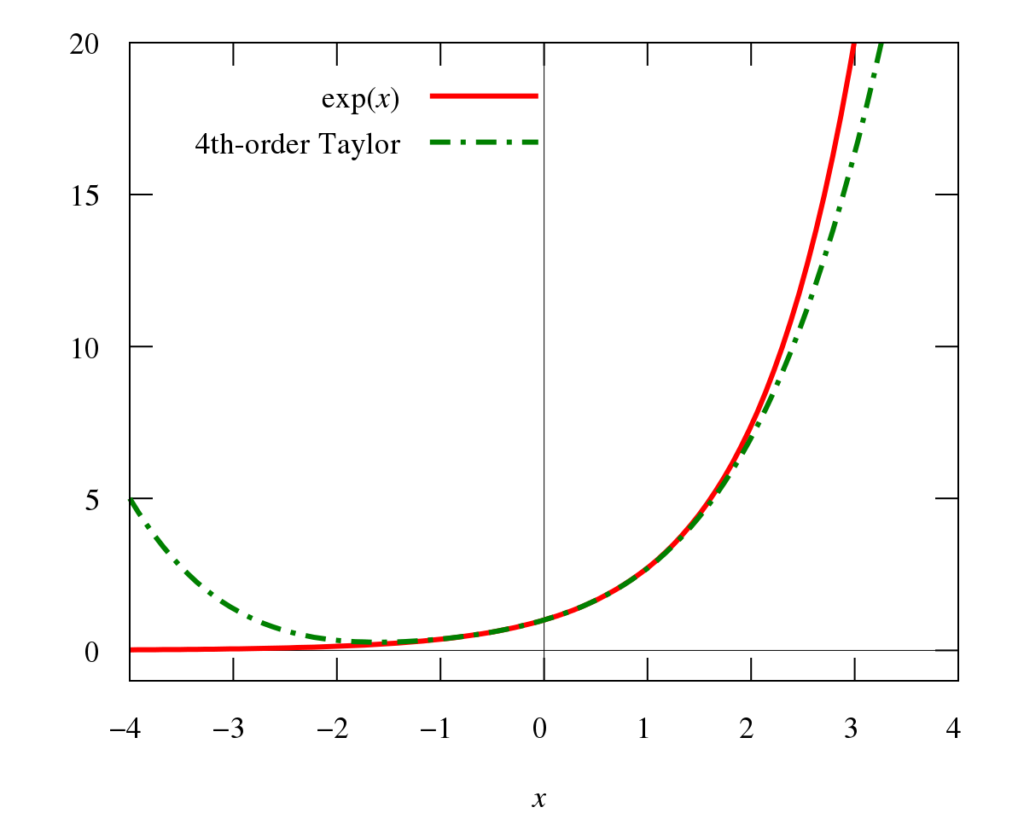
Chas, $f$ is infinitely differentiable in $\mathbb{R} \mathrm{~ . ~ W e s e r e}$ Example 2.3.31 Let $f(x)=e^{x}, x \in \mathbb{R}$. We know that $f^{\prime}(x)=e^{x}$. Hence, it follows that $f^{(k)}(x)=e^{x}$ for every $k \in \mathbb{N}$ so that $f$ is infinitely differentiable in $\mathbb{R}$. $\nabla$
定义 2.3.7 让F定义在开区间一世. 那么,对于到∈ñ和到≥2,F据说是到时间可微X0∈一世如果F(1)(X),F(2)(X),…,F(到−1)(X)被迭代定义为
F(j)(X):=[F(j−1)]′(X),j=1,…,到−1
154 2 函数的
极限、连续性和可微性
X在附近X0和F(0)(X)=F(X)和
F(到)(X0):=[F(到−1)]′(X0)
存在。然后F(到)(X0)被称为到th -衍生物F在X0.
注意F(2)(X0)是的二阶导数F在X0. 这到th -衍生物F也表示为
d到FdX到
也习惯用记号DF为了F′和D到F为了F(到),所以它是D到F=D(D到−1F).
定义 2.3.8 函数F据说在一点上是无限可微的X0∈一世如果F已到th -衍生于X0对于每个到∈ñ.
我们可能会观察到以下情况:如果F在一点上是无限可微的X0∈一世,那么对于每个到∈ñ,F已到th -导数不仅在X0但也在某个街区的每一点X0. 示例 2.3.29 对于n∈ñ, 让F(X)=Xn,X∈R. 然后我们知道F(1)(X)= F′(X)=nXn−1. 因此,对于到≤n, 我们有F(到)(X)=n(n−1)⋯(n−到+1)Xn−到和F(到)(X)=0为了到>n. 因此,F是无限可微的R. 更一般地说,如果F是多项式,那么F是无限可微的R.
示例 2.3.30 让F(X)=没有X,X∈R. 然后我们有
F(1)(X)=某物X,F(2)(X)=−没有X,F(3)(X)=−某物X,F(4)(X)=没有X
更一般地,对于任何到∈ñ,
F(2到−1)(X)=(−1)到+1某物X,F(2到)(X)=(−1)到没有X.
因此,F是无限可微的R.
查斯,F是无限可微的R . 在和s和r和示例 2.3.31 让F(X)=和X,X∈R. 我们知道F′(X)=和X. 因此,由此得出F(到)(X)=和X对于每个到∈ñ以便F是无限可微的R.∇

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。