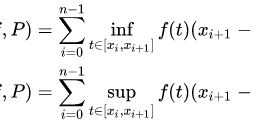$8.1$
Functions Defined in Terms of Series
It is time to consider functions other than polynomials. In particular it is time to give a mathematically acceptable definition of functions like $e^{x}, \sin (x)$ and $\cos (x)$. It has been assumed these functions are known from beginning calculus but this is a pretence. Most students who take calculus come through it without a complete understanding of the circular functions. This is because of the reliance on plane geometry in defining them. Fortunately, these functions can be completely understood in terms of power series rather than wretched plane geometry. The exponential function can also be defined in a simple manner using power series. It is tacitly assumed in this presentation that $x \in \mathbb{F}$, either $\mathbb{R}$ or $\mathbb{C}$.
Definition 8.1.1 Let $\left{a_{k}\right}_{k=0}^{\infty}$ be a sequence of numbers. The expression,
$$
\sum_{k=0}^{\infty} a_{k}(x-a)^{k}
$$
is called a Taylor series centered at a. This is also called a power series centered at a. It is understood that $x$ and $a \in \mathbb{F}$, that is, either $\mathbb{C}$ or $\mathbb{R}$.
In the above definition, $x$ is a variable. Thus you can put in various values of $x$ and ask whether the resulting series of numbers converges. Defining $D$ to be the set of all values of $x$ such that the resulting series does converge, define a new function $f$ defined on $D$ having values in $\mathbb{F}$ as $f(x) \equiv \sum_{k=0}^{\infty} a_{k}(x-a)^{k}$. This might be a totally new function, one which has no name. Nevertheless, much can be said about such functions. The following lemma is fundamental in considering the form of $D$ which always turns out to be of the form $B(a, r)$ along with possibly some points $z$ such that $|z-a|=r$. First here is a simple lemma which will be useful.
Lemma 8.1.2 $\lim {n \rightarrow \infty} n^{1 / n}=1$. Proof: It is clear $n^{1 / n} \geq 1$. Let $n^{1 / n}=1+e{n}$ where $0 \leq e_{n}$. Then raising both sides to the $n^{t h}$ power for $n>1$ and using the binomial theorem,
$$
n=\left(1+e_{n}\right)^{n}=\sum_{k=0}^{n}\left(\begin{array}{l}
n \
k
\end{array}\right) e_{n}^{k} \geq 1+n e_{n}+(n(n-1) / 2) e_{n}^{2} \geq(n(n-1) / 2) e_{n}^{2}
$$
Thus $0 \leq e_{n}^{2} \leq \frac{n}{n(n-1)}=\frac{1}{n-1}$. From this the desired result follows because $\left|n^{1 / n}-1\right|=$ $e_{n} \leq \frac{1}{\sqrt{n-1}} .$
151
Theorem 8.1.3 Let $\sum_{k=0}^{\infty} a_{k}(x-a)^{k}$ be a Taylor series. Then there exists $r \leq \infty$ such that the Taylor series converges absolutely if $|x-a|r$, the Taylor series diverges. If $\lambda<r$ then the Taylor series converges uniformly on the closed disk $|x-a| \leq \lambda$.
Proof: Note $\limsup {k \rightarrow \infty}\left|a{k}(x-a)^{k}\right|^{1 / k}=\limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}|x-a|$. Then by the root test, the series converges absolutely if $|x-a| \lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}<1$ and diverges if $|x-a| \limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}>1$. Thus define $$ r \equiv\left{\begin{array}{l}1 / \limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} \text { if } \infty>\lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}>0 \ \infty \text { if } \lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}=0 \ 0 \text { if } \limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}=\infty\end{array}\right. $$
$r \equiv\left{\begin{array}{l}1 / \limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} \text { if } \infty>\lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}>0 \ \infty \text { if } \lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}=0 \ 0 \text { if } \limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}=\infty\end{array}\right.$ be as described. Then if $|x-a| \leq \lambda$, then $\left|a_{k}(x-a)^{k}\right|^{1 / k}=\lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}|x-a| \leq \lambda \lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} \leq \frac{\lambda}{r}<\alpha<1$ Next let $\lambda$ be as described. Then if $|x-a| \leq \lambda$, then $$ \lim \sup {k \rightarrow \infty}\left|a{k}(x-a)^{k}\right|^{1 / k}=\lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}|x-a| \leq \lambda \lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} \leq \frac{\lambda}{r}<\alpha<1 $$ It follows that for all $k$ large enough and such $x,\left|a_{k}(x-a)^{k}\right|<\alpha^{k}$. Then by the Weierstrass $M$ test, convergence is uniform. Note that the radius of convergence $r$ is given by $\lim \sup _{k \rightarrow \infty}\left|a_{k}\right|^{1 / k} r=1$ Definition 8.1.4 The number in the above theorem is called the radius of convergence and the set on which convergence takes place is called the disc of convergence. Now the theorem was proved using the root test but often you use the ratio test to find the radius of convergence. This kind of thing is typical in math and one must adjust to this fact. The proof of a theorem does not always yield a way to find the thing the theorem speaks about. The above is an existence theorem. There exists a disk of convergence from the above theorem. You find it in specific cases any way that is most convenient. Example 8.1.5 Find the disc of convergence of the Taylor series $\sum_{n=1}^{\infty} \frac{x^{n}}{n}$. Use Corollary 5.4.10. $\lim _{n \rightarrow \infty}\left(\frac{|x|^{n}}{n}\right)^{1 / n}=\lim _{n \rightarrow \infty} \frac{|x|}{\sqrt[n]{n}}=|x|$ because $\lim _{n \rightarrow \infty} \sqrt[n]{n}=$ 1 and so if $|x|<1$ the series converges. The points satisfying $|z|=1$ require special attention. When $x=1$ the series diverges because it reduces to $\sum_{n=1}^{\infty} \frac{1}{n} .$ At $x=-1$ the series converges because it reduces to $\sum_{n=1}^{\infty} \frac{(-1)^{n}}{n}$ and the alternating series test applies and gives convergence. What of the other numbers $z$ satisfying $|z|=1 ?$ It turns out this series will converge at all these numbers by the Dirichlet test. Example 8.1.6 Find the radius of convergence of $\sum_{n=1}^{\infty} \frac{n^{n}}{n !} x^{n}$. Apply the ratio test. Taking the ratio of the absolute values of the $(n+1)^{t h}$ and the $n^{\text {th }}$ terms $$ \frac{\frac{(n+1)^{(n+1)}}{(n+1) n !}|x|^{n+1}}{\frac{n^{n}}{n !}|x|^{n}}=(n+1)^{n}|x| n^{-n}=|x|\left(1+\frac{1}{n}\right)^{n} \rightarrow|x| e $$ Therefore the series converges absolutely if $|x| e<1$ and diverges if $|x| e>1$. Consequently, $r=1 / e$. This problem assumes that you remember from calculus the last limit. If not, this will be discussed later.
用序列定义的函数
是时候考虑多项式以外的函数了。尤其是对 $e^{x}、\sin (x)$ 和 $\cos (x)$ 等函数给出数学上可接受的定义的时候了。假设这些函数从一开始就知道微积分,但这是一个幌子。大多数学习微积分的学生都没有完全理解循环函数。这是因为在定义它们时依赖于平面几何。幸运的是,这些函数可以完全用幂级数而不是可怜的平面几何来理解。指数函数也可以使用幂级数以简单的方式定义。在此演示文稿中默认 $x \in \mathbb{F}$,$\mathbb{R}$ 或 $\mathbb{C}$。
定义 8.1.1 令 $\left{a_{k}\right}_{k=0}^{\infty}$ 是一个数字序列。表达方式,
$$
\sum_{k=0}^{\infty} a_{k}(x-a)^{k}
$$
称为以 a 为中心的泰勒级数。这也称为以 a 为中心的幂级数。可以理解为$x$和$a\in\mathbb{F}$,即$\mathbb{C}$或者$\mathbb{R}$。
在上面的定义中,$x$ 是一个变量。因此,您可以输入 $x$ 的各种值并询问所得的数字序列是否收敛。将 $D$ 定义为 $x$ 的所有值的集合,这样结果级数确实会收敛,定义一个在 $D$ 上定义的新函数 $f$,其值在 $\mathbb{F}$ 为 $f(x ) \equiv \sum_{k=0}^{\infty} a_{k}(xa)^{k}$。这可能是一个全新的功能,没有名称。然而,关于这些功能可以说很多。下面的引理是考虑 $D$ 的形式的基础,它总是变成 $B(a, r)$ 的形式,可能还有一些点 $z$ 使得 $|z-a|=r$。首先是一个简单的引理,它很有用。
引理 8.1.2 $\lim {n \rightarrow \infty} n^{1 / n}=1$。 证明:显然 $n^{1 / n} \geq 1$。令 $n^{1 / n}=1+e{n}$ 其中 $0 \leq e_{n}$。然后将两边都提升到 $n^{th}$ 的幂 $n>1$ 并使用二项式定理,
$$
n=\left(1+e_{n}\right)^{n}=\sum_{k=0}^{n}\left(\begin{array}{l}
n \
ķ
\end{数组}\right) e_{n}^{k} \geq 1+n e_{n}+(n(n-1) / 2) e_{n}^{2} \geq(n(n -1) / 2) e_{n}^{2}
$$
因此 $0 \leq e_{n}^{2} \leq \frac{n}{n(n-1)}=\frac{1}{n-1}$。由此得到期望的结果,因为 $\left|n^{1 / n}-1\right|=$ $e_{n} \leq \frac{1}{\sqrt{n-1}} .$
151
定理 8.1.3 令 $\sum_{k=0}^{\infty} a_{k}(x-a)^{k}$ 为泰勒级数。那么存在 $r \leq \infty$ 使得泰勒级数绝对收敛,如果 $|x-a|r$,泰勒级数发散。如果 $\lambda<r$ 则泰勒级数均匀收敛于闭盘 $|x-a| \leq \lambda$。
证明:注 $\limsup {k \rightarrow \infty}\left|a{k}(xa)^{k}\right|^{1 / k}=\limsup {k \rightarrow \infty}\left |a{k}\right|^{1 / k}|xa|$.然后通过根检验,如果 $|x-a| 则级数绝对收敛\lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}<1$ 并且如果 $|x-a| 发散\limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}>1$。因此定义 $$ r \equiv\left{\begin{array}{l}1 / \limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} \text {如果 } \infty>\lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}>0 \ \infty \text { 如果 } \lim \sup { k \rightarrow \infty}\left|a{k}\right|^{1 / k}=0 \ 0 \text { if } \limsup {k \rightarrow \infty}\left|a{k}\对|^{1 / k}=\infty\end{array}\right. $$
$r \equiv\left{\begin{array}{l}1 / \limsup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} \text { if } \ infty>\lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}>0 \ \infty \text { if } \lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k}=0 \ 0 \text { if } \limsup {k \rightarrow \infty}\left|a{k}\right|^ {1 / k}=\infty\end{array}\right.$ 如所述。那么如果 $|x-a| \leq \lambda$,然后 $\left|a_{k}(xa)^{k}\right|^{1 / k}=\lim \sup {k \rightarrow \infty}\left|a{k }\right|^{1 / k}|xa| \leq \lambda \lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} \leq \frac{\lambda}{r}<\alpha<1$
接下来让 $\lambda$ 如所描述的那样。那么如果 $|x-a| \leq \lambda$,然后 $$ \lim \sup {k \rightarrow \infty}\left|a{k}(xa)^{k}\right|^{1 / k}=\lim \sup _ {k \rightarrow \infty}\left|a_{k}\right|^{1 / k}|xa| \leq \lambda \lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} \leq \frac{\lambda}{r}<\alpha<1 $$因此对于所有足够大的 $k$ 和这样的 $x,\left|a_{k}(xa)^{k}\right|<\alpha^{k}$。然后通过 Weierstrass $M$ 测试,收敛是一致的。
请注意,收敛半径 $r$ 由 $\lim \sup {k \rightarrow \infty}\left|a{k}\right|^{1 / k} r=1$ 给出
定义 8.1.4 上述定理中的数字称为收敛半径,发生收敛的集合称为收敛圆盘。
现在使用根检验证明了该定理,但通常您使用比率检验来找到收敛半径。这种东西在垫子上很典型

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。