统计代写| Discrete Uniform stat代写
统计代考
3.5 Discrete Uniform
A very simple story, closely connected to the naive definition of probability, describes picking a random number from some finite set of possibilities.
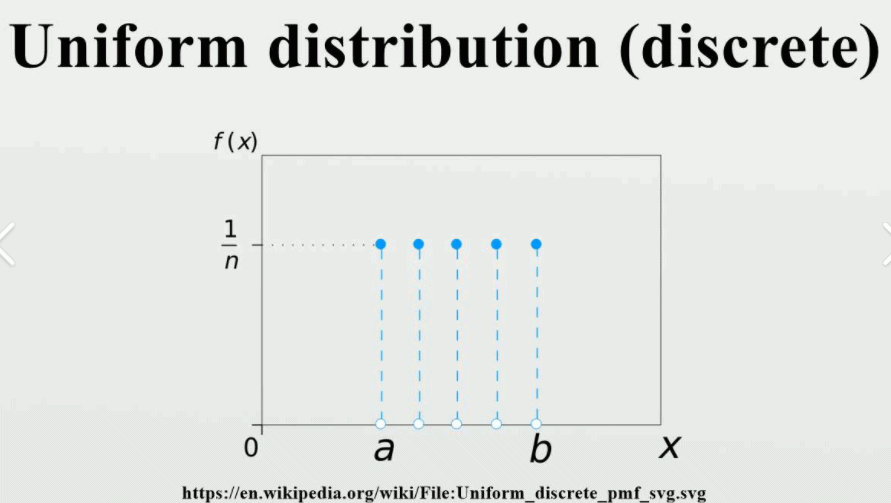
Story 3.5.1 (Discrete Uniform distribution). Let $C$ be a finite, nonempty set of numbers. Choose one of these numbers uniformly at random (i.e., all values in $C$ are equally likely). Call the chosen number $X$. Then $X$ is said to have the Discrete Uniform distribution with parameter $C$; we denote this by $X \sim \mathrm{DUnif}(C)$.
The PMF of $X \sim \operatorname{DUnif}(C)$ is
$$
P(X=x)=\frac{1}{|C|}
$$
for $x \in C$ (and 0 otherwise), since a PMF must sum to 1. As with questions based on the naive definition of probability, questions based on a Discrete Uniform distribution reduce to counting problems. Specifically, for $X \sim \mathrm{DUnif}(C)$ and any $A \subseteq C$, we have
$$
P(X \in A)=\frac{|A|}{|C|} .
$$
119
Random variables and their distributions
Example 3.5.2 (Random slips of paper). There are 100 slips of paper in a hat, each of which has one of the numbers $1,2, \ldots, 100$ written on it, with no number appearing more than once. Five of the slips are drawn, one at a time.
First consider random sampling with replacement (with equal probabilities).
(a) What is the distribution of how many of the drawn slips have a value of at least 80 written on them?
(b) What is the distribution of the value of the $j$ th draw (for $1 \leq j \leq 5) ?$
(c) What is the probability that the number 100 is drawn at least once?
Now consider random sampling without replacement (with all sets of five slips equally likely to be chosen).
(d) What is the distribution of how many of the drawn slips have a value of at least 80 written on them?
(e) What is the distribution of the value of the $j$ th draw (for $1 \leq j \leq 5) ?$
(f) What is the probability that the number 100 is drawn in the sample?
Solution:
(a) By the story of the Binomial, the distribution is $\operatorname{Bin}(5,0.21)$.
(b) Let $X_{j}$ be the value of the $j$ th draw. By symmetry, $X_{j} \sim \operatorname{DUnif}(1,2, \ldots, 100) .$ There aren’t certain slips that love being chosen on the $j$ th draw and others that avoid being chosen then; all are equally likely.
(c) Taking complements,
$$
P\left(X_{j}=100 \text { for at least one } j\right)=1-P\left(X_{1} \neq 100, \ldots, X_{5} \neq 100\right)
$$
By the naive definition of probability, this is
$$
1-(99 / 100)^{5} \approx 0.049
$$
This solution just uses new notation for concepts from Chapter 1 . It is useful to have this new notation since it is compact and flexible. In the above calculation, it is important to see why
$$
P\left(X_{1} \neq 100, \ldots, X_{5} \neq 100\right)=P\left(X_{1} \neq 100\right) \ldots P\left(X_{5} \neq 100\right)
$$
This follows from the naive definition in this case, but a more general way to think about such statements is through independence of r.v.s, a concept discussed in detail in Section 3.8.
(d) By the story of the Hypergeometric, the distribution is HGeom(21, 79,5).
(e) Let $Y_{j}$ be the value of the $j$ th draw. By symmetry, $Y_{j} \sim \operatorname{DUnif}(1,2, \ldots, 100)$.
统计代考
3.5 离散均匀
一个非常简单的故事,与概率的朴素定义密切相关,描述了从一些有限的可能性集合中选择一个随机数。
故事 3.5.1(离散均匀分布)。令$C$ 是一个有限的、非空的数字集。随机均匀地选择其中一个数字(即,$C$ 中的所有值的可能性相同)。拨打所选号码 $X$。那么 $X$ 被称为具有参数 $C$ 的离散均匀分布;我们用 $X \sim \mathrm{DUnif}(C)$ 来表示它。
$X \sim \operatorname{DUnif}(C)$ 的 PMF 是
$$
P(X=x)=\frac{1}{|C|}
$$
对于 $x \in C$(否则为 0),因为 PMF 的总和必须为 1。与基于朴素概率定义的问题一样,基于离散均匀分布的问题减少为计数问题。具体来说,对于 $X \sim \mathrm{DUnif}(C)$ 和任何 $A \subseteq C$,我们有
$$
P(X \in A)=\frac{|A|}{|C|} 。
$$
119
随机变量及其分布
示例 3.5.2(随机纸条)。一顶帽子里有 100 张纸条,每张纸条上都写着 $1,2, \ldots, 100$ 中的一个,没有一个数字出现超过一次。抽出五张纸条,一次一张。
首先考虑带放回的随机抽样(概率相等)。
(a) 有多少已抽出的单据上写有至少 80 的值,分布情况如何?
(b) 第 $j$ 次抽奖的价值分布是什么(对于 $1 \leq j \leq 5)?$
(c) 数字 100 至少被抽中一次的概率是多少?
现在考虑无放回的随机抽样(所有五张单据组均等可能被选中)。
(d) 有多少已抽出的单据上写的值至少为 80,分布情况如何?
(e) 第 $j$ 次抽奖的价值分布是什么(对于 $1 \leq j \leq 5)?$
(f) 在样本中抽取数字 100 的概率是多少?
解决方案:
(a) 根据二项式的故事,分布是 $\operatorname{Bin}(5,0.21)$。
(b) 令 $X_{j}$ 为第 $j$ 次抽奖的价值。通过对称性,$X_{j} \sim \operatorname{DUnif}(1,2, \ldots, 100) .$ 在第 $j$ 次抽签中,没有特定的纸条喜欢被选中,而其他纸条则避免被选中然后;所有的可能性都是一样的。
(c) 取补,
$$
P\left(X_{j}=100 \text { 对于至少一个 } j\right)=1-P\left(X_{1} \neq 100, \ldots, X_{5} \neq 100\right)
$$
根据概率的朴素定义,这是
$$
1-(99 / 100)^{5} \约 0.049
$$
这个解决方案只是对第 1 章中的概念使用了新的符号。拥有这种新符号很有用,因为它紧凑且灵活。在上面的计算中,重要的是要看看为什么
$$
P\left(X_{1} \neq 100, \ldots, X_{5} \neq 100\right)=P\left(X_{1} \neq 100\right) \ldots P\left(X_{5} \neq 100\右)
$$
这是从本例中的幼稚定义得出的,但考虑此类陈述的更一般的方法是通过 r.v.s 的独立性,这是第 3.8 节中详细讨论的概念。
(d) 根据超几何的故事,分布是 HGeom(21, 79,5)。
(e) 设 $Y_{j}$ 为第 $j$ 次抽奖的价值。通过对称性,$Y_{j} \sim \operatorname{DUnif}(1,2, \ldots, 100)$。
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。