统计代写| Expectations and variances stat代写
统计代考
11.2 Classification of states
In this section we introduce terminology for describing the various characteristics of a Markov chain. The states of a Markov chain can be classified as recurrent or transient, depending on whether they are visited over and over again in the long run or are eventually abandoned. States can also be classified according to their period, which is a positive integer summarizing the amount of time that can elapse between successive visits to a state. These characteristics are important because they determine the long-run behavior of the Markov chain, which we will study in they determi Section $11.3$.
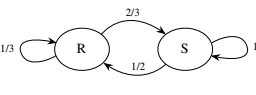
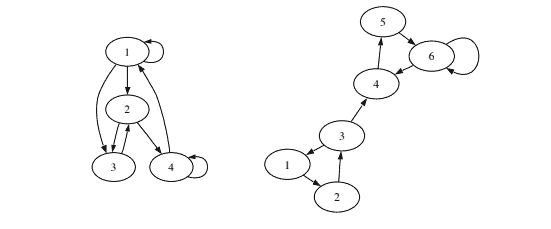
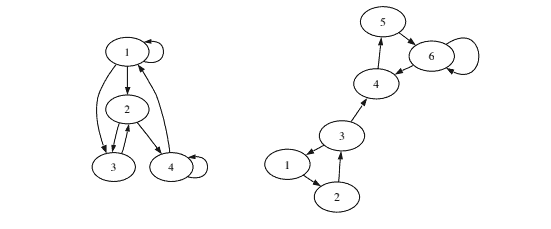
The concepts of recurrence and transience are best illustrated with a concrete example. In the Markov chain shown on the left of Figure 11.2 (previously featured in Example 11.1.5), a particle moving around between states will continue to spend time in all 4 states in the long run, since it is possible to get from any state to any other state. In contrast, consider the chain on the right of Figure 11.2, and let the particle start at state 1 . For a while, the chain may linger in the triangle formed by states 1,2, and 3, but eventually it will reach state 4, and from there it can never states 1,2, and 3, but eventually it will reach state 4, and from there it can never return to states 1,2, or 3 . It will then wander around between states 4,5, and 6 return to states 1,2, or $3 .$ it will then wander around between states 4,5, forever. States 1,2, and 3 are transient and states 4,5, and 6 are recurrent.
In general, these concepts are defined as follows.
503
Markov chains
FIGURE 11.2
Left: 4-state Markov chain with all states recurrent. Right: 6-state Markov chain with states 1,2 , and 3 transient.
Definition 11.2.1 (Recurrent and transient states). State $i$ of a Markov chain is recurrent if starting from $i$, the probability is 1 that the chain will eventually return to $i$. Otherwise, the state is transient, which means that if the chain starts from $i$, there is a positive probability of never returning to $i$.
In fact, although the definition of a transient state only requires that there be a positive probability of never returning to the state, we can say something stronger: as long as there is a positive probability of leaving $i$ forever, the chain eventually will leave $i$ forever. Moreover, we can find the distribution of the number of returns to the state.
Proposition 11.2.2 (Number of returns to transient state is Geometric). Let $i$ be a transient state of a Markov chain. Suppose the probability of never returning to $i$, starting from $i$, is a positive number $p>0$. Then, starting from $i$, the number of times that the chain returns to $i$ before leaving forever is distributed $\operatorname{Geom}(p)$.
The proof is by the story of the Geometric distribution: each time that the chain is at $i$, we have a Bernoulli trial which results in “failure” if the chain eventually returns to $i$ and “success” if the chain leaves $i$ forever; these trials are independent by the Markov property. The number of returns to state $i$ is the number of failures since a Geometric random variable always takes finite values, this proposition tells us that after some finite number of visits, the chain will leave state $i$ forever.
If the number of states is not too large, one way to classify states as recurrent or transient is to draw a diagram of the Markov chain and use the same kind of reasoning that we used when analyzing the chains in Figure 11.2. A special case where we can immediately conclude all states are recurrent is when the chain is irreducible, meaning that it is possible to get from any state to any other state.
统计代考
11.2 状态分类
在本节中,我们将介绍用于描述马尔可夫链的各种特征的术语。马尔可夫链的状态可以分为周期性的或瞬态的,这取决于它们是在长期内被一遍又一遍地访问还是最终被放弃。状态也可以根据它们的周期进行分类,周期是一个正整数,总结了连续访问一个状态之间可以经过的时间量。这些特征很重要,因为它们决定了马尔可夫链的长期行为,我们将在第 11.3 节中研究它们。
用一个具体的例子来最好地说明重复和短暂的概念。在图 11.2 左侧所示的马尔可夫链中(以前在示例 11.1.5 中展示过),从长远来看,在状态之间移动的粒子将继续在所有 4 个状态中花费时间,因为它可以从任何状态得到到任何其他状态。相反,考虑图 11.2 右边的链,让粒子从状态 1 开始。有一段时间,链可能会在状态 1,2 和 3 形成的三角形中徘徊,但最终它会到达状态 4,从那里它永远不会状态 1,2 和 3,但最终它会到达状态 4 ,并且从那里它永远不会返回到状态 1,2 或 3 。然后它将在状态 4,5 和 6 之间徘徊,返回状态 1,2,或 $3 .$ 然后它将永远在状态 4,5 之间徘徊。状态 1,2 和 3 是短暂的,而状态 4,5 和 6 是经常性的。
一般来说,这些概念定义如下。
503
马尔可夫链
图 11.2
左:所有状态循环的 4 状态马尔可夫链。右图:具有状态 1,2 和 3 瞬态的 6 状态马尔可夫链。
定义 11.2.1(循环和瞬态)。马尔可夫链的状态 $i$ 是循环的,如果从 $i$ 开始,该链最终返回 $i$ 的概率为 1。否则,状态是瞬态的,这意味着如果链从 $i$ 开始,则永远不会返回 $i$ 的概率为正。
事实上,虽然瞬态的定义只要求有一个永远不会返回该状态的正概率,但我们可以说更强一点:只要有一个永远离开$i$的正概率,链最终会永远离开$i$。此外,我们可以找到返回状态的数量分布。
命题 11.2.2(返回瞬态的次数是几何的)。令$i$ 为马尔可夫链的瞬态。假设从$i$开始永远不会返回$i$的概率是一个正数$p>0$。然后,从$i$开始,链在永远离开之前返回$i$的次数分布$\operatorname{Geom}(p)$。
证明是几何分布的故事:每次链在 $i$ 时,我们都会进行伯努利试验,如果链最终返回 $i$,则导致“失败”,如果链离开,则导致“成功” $i$ 永远;这些试验独立于马尔可夫性质。返回状态 $i$ 的次数是失败的次数,因为几何随机变量总是取有限值,这个命题告诉我们,在有限次数的访问之后,链将永远离开状态 $i$。
如果状态的数量不太大,将状态分类为循环或瞬态的一种方法是绘制马尔可夫链图,并使用我们在分析图 11.2 中的链时使用的相同推理。我们可以立即断定所有状态都是循环的一个特殊情况是当链不可约时,这意味着有可能从任何状态到达任何其他状态。
。
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。