统计代写| Functions of random variables stat代写
统计代考
3.7 Functions of random variables
In this section we will discuss what it means to take a function of a random variable, and we will build understanding for why a function of a random variable is a random variable. That is, if $X$ is a random variable, then $X^{2}, e^{X}$, and $\sin (X)$ are also random variables, as is $g(X)$ for any function $g: \mathbb{R} \rightarrow \mathbb{R}$.
For example, imagine that two basketball teams (A and B) are playing a sevengame match, and let $X$ be the number of wins for team A (so $X \sim \operatorname{Bin}(7,1 / 2)$ if the teams are evenly matched and the games are independent). Let $g(x)=7-x$, and let $h(x)=1$ if $x \geq 4$ and $h(x)=0$ if $x<4$. Then $g(X)=7-X$ is the number of wins for team $\mathrm{B}$, and $h(X)$ is the indicator of team A winning the majority of the games. Since $X$ is an r.v., both $g(X)$ and $h(X)$ are also r.v.s.
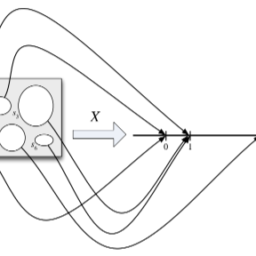
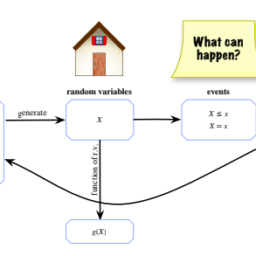
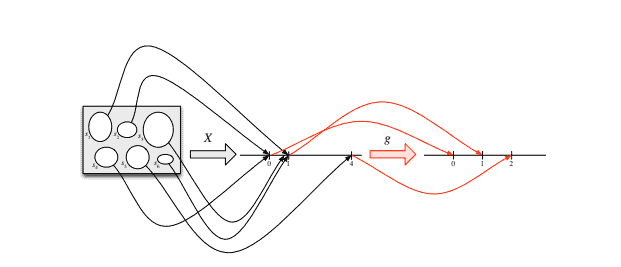
To see how to define functions of an r.v. formally, let’s rewind a bit. At the beginning of this chapter, we considered a random variable $X$ defined on a sample space with 6 elements. Figure $3.1$ used arrows to illustrate how $X$ maps each pebble in the sample space to a real number, and the left half of Figure $3.2$ showed how we can equivalently imagine $X$ writing a real number inside each pebble.
Now we can, if we want, apply the same function $g$ to all the numbers inside the pebbles. Instead of the numbers $X\left(s_{1}\right)$ through $X\left(s_{6}\right)$, we now have the numbers $g\left(X\left(s_{1}\right)\right)$ through $g\left(X\left(s_{6}\right)\right)$, which gives a new mapping from sample outcomes to real numbers – we’ve created a new random variable, $g(X)$.
Definition 3.7.1 (Function of an r.v.). For an experiment with sample space $S$, an r.v. $X$, and a function $g: \mathbb{R} \rightarrow \mathbb{R}, g(X)$ is the r.v. that maps $s$ to $g(X(s))$ for all $s \in S$.
Taking $g(x)=\sqrt{x}$ for concreteness, Figure $3.9$ shows that $g(X)$ is the composition of the functions $X$ and $g$, saying “first apply $X$, then apply $g$ “. Figure $3.10$ represents $g(X)$ more succinctly by directly labeling the sample outcomes. Both figures show us that $g(X)$ is an r.v.; if $X$ crystallizes to 4 , then $g(X)$ crystallizes to 2 .
Given a discrete r.v. $X$ with a known PMF, how can we find the PMF of $Y=g(X)$ ? In the case where $g$ is a one-to-one function, the answer is straightforward: the support of $Y$ is the set of all $g(x)$ with $x$ in the support of $X$, and
$$
P(Y=g(x))=P(g(X)=g(x))=P(X=x) .
$$
124
FIGURE $3.9$
The r.v. $X$ is defined on a sample space with 6 elements, and has possible values 0 , 1 , and 4 . The function $g$ is the square root function. Composing $X$ and $g$ gives the random variable $g(X)=\sqrt{X}$, which has possible values 0,1 , and 2 .
Random variables and their distributions
125
The case where $Y=g(X)$ with $g$ one-to-one is illustrated in the following tables; the idea is that if the distinct possible values of $X$ are $x_{1}, x_{2}, \ldots$ with probabilities $p_{1}, p_{2}, \ldots$ (respectively), then the distinct possible values of $Y$ are $g\left(x_{1}\right), g\left(x_{2}\right), \ldots$, with the same list $p_{1}, p_{2}, \ldots$ of probabilities.
\begin{tabular}{ccccc}
\hline$x$ & $P(X=x)$ & & $y$ & $P(Y=y)$ \
\hline$x_{1}$ & $p_{1}$ & & $g\left(x_{1}\right)$ & $p_{1}$ \
$x_{2}$ & $p_{2}$ & & $g\left(x_{2}\right)$ & $p_{2}$ \
$x_{3}$ & $p_{3}$ & & $g\left(x_{3}\right)$ & $p_{3}$ \
$\vdots$ & $\vdots$ & & $\vdots$ & $\vdots$ \
\hline
\end{tabular}
This suggests a strategy for finding the PMF of an r.v. with an unfamiliar distribution: try to express the r.v. as a one-to-one function of an r.v. with a known distribution. The next example illustrates this method.
Example 3.7.2 (Random walk). A particle moves $n$ steps on a number line. The particle starts at 0 , and at each step it moves 1 unit to the right or to the left, with equal probabilities. Assume all steps are independent. Let $Y$ be the particle’s position after $n$ steps. Find the PMF of $Y$.
Solution:
Consider each step to be a Bernoulli trial, where right is considered a success and left is considered a failure. Then the number of steps the particle takes to the right is a $\operatorname{Bin}(n, 1 / 2)$ random variable, which we can name $X$. If $X=j$, then the particle has taken $j$ steps to the right and $n-j$ steps to the left, giving a final position of $j-(n-j)=2 j-n .$ So we can express $Y$ as a one-to-one function of $X$, namely, $Y=2 X-n$. Since $X$ takes values in ${0,1,2, \ldots, n}, Y$ takes values in ${-n, 2-n, 4-n, \ldots, n} .$
The PMF of $Y$ can then be found from the PMF of $X$ :
$$
P(Y=k)=P(2 X-n=k)=P(X=(n+k) / 2)=\left(\begin{array}{c}
n \
\frac{n+k}{2}
\end{array}\right)\left(\frac{1}{2}\right)^{n}
$$
if $k$ is an integer between $-n$ and $n$ (inclusive) such that $n+k$ is an even number.
If $g$ is not one-to-one, then for a given $y$, there may be multiple values of $x$ such that $g(x)=y$. To compute $P(g(X)=y)$, we need to sum up the probabilities of $X$ taking on any of these candidate values of $x$.
Theorem 3.7.3 (PMF of $g(X)$ ). Let $X$ be a discrete r.v. and $g: \mathbb{R} \rightarrow \mathbb{R}$. Then the support of $g(X)$ is the set of all $y$ such that $g(x)=y$ for at least one $x$ in the support of $X$, and the PMF of $g(X)$ is
$$
P(g(X)=y)=\sum_{x: g(x)=y} P(X=x),
$$
126
for all $y$ in the support of $g(X)$.
统计代考
3.7 随机变量的函数
在本节中,我们将讨论取随机变量函数的含义,并理解为什么随机变量的函数是随机变量。也就是说,如果 $X$ 是一个随机变量,那么 $X^{2}、e^{X}$ 和 $\sin (X)$ 也是随机变量,对于任何函数 $g: \mathbb{R} \rightarrow \mathbb{R}$。
例如,假设两支篮球队(A 和 B)正在进行七场比赛,设 $X$ 为 A 队的获胜次数(所以 $X \sim \operatorname{Bin}(7,1 / 2) $ 如果球队势均力敌并且比赛是独立的)。令$g(x)=7-x$,如果$x \geq 4$,则令$h(x)=1$,如果$x<4$,则令$h(x)=0$。那么 $g(X)=7-X$ 是 $\mathrm{B}$ 队的获胜次数,$h(X)$ 是 A 队赢得大部分比赛的指标。由于 $X$ 是 r.v.,$g(X)$ 和 $h(X)$ 也是 r.v.s。
了解如何定义房车的功能。正式地,让我们倒带一下。在本章的开头,我们考虑了一个定义在一个有 6 个元素的样本空间上的随机变量 $X$。图 $3.1$ 使用箭头说明 $X$ 如何将样本空间中的每个卵石映射到一个实数,图 $3.2$ 的左半部分显示了我们如何等效地想象 $X$ 在每个卵石中写入一个实数。
现在,如果我们愿意,我们可以将相同的函数 $g$ 应用于鹅卵石内的所有数字。我们现在有数字 $g\left(X\left(s_{1} \right)\right)$ 到 $g\left(X\left(s_{6}\right)\right)$,它给出了从样本结果到实数的新映射——我们创建了一个新的随机变量, $g(X)$。
定义 3.7.1(房车的功能)。对于样本空间 $S$ 的实验,一个 r.v. $X$, 和一个函数 $g: \mathbb{R} \rightarrow \mathbb{R}, g(X)$ 是 r.v。将所有 $s \in S$ 的 $s$ 映射到 $g(X(s))$。
以 $g(x)=\sqrt{x}$ 为具体,图 $3.9$ 表明 $g(X)$ 是函数 $X$ 和 $g$ 的组合,表示“首先应用 $X$,然后申请$g$”。图 $3.10$ 通过直接标记样本结果更简洁地表示 $g(X)$。这两个数字都向我们展示了 $g(X)$ 是一个 r.v.;如果 $X$ 结晶为 4 ,则 $g(X)$ 结晶为 2 。
给定一个离散的 r.v. $X$ 具有已知的 PMF,我们如何找到 $Y=g(X)$ 的 PMF?在 $g$ 是一对一函数的情况下,答案很简单:$Y$ 的支持是所有 $g(x)$ 的集合,$x$ 在 $X$ 的支持下,和
$$
P(Y=g(x))=P(g(X)=g(x))=P(X=x) 。
$$
124
图 $3.9$
房车$X$ 是在具有 6 个元素的样本空间上定义的,可能的值是 0 、 1 和 4 。函数 $g$ 是平方根函数。组合 $X$ 和 $g$ 给出随机变量 $g(X)=\sqrt{X}$,其可能值为 0,1 和 2 。
随机变量及其分布
125
$Y=g(X)$ 与 $g$ 一对一的情况如下表所示;这个想法是,如果 $X$ 的不同可能值是 $x_{1}、x_{2}、\ldots$,概率分别为 $p_{1}、p_{2}、\ldots$,那么$Y$ 的不同可能值为 $g\left(x_{1}\right)、g\left(x_{2}\right)、\ldots$,具有相同的列表 $p_{1}、p_{2 }, \ldots$ 的概率。
\开始{表格}{ccccc}
\hline$x$ & $P(X=x)$ & & $y$ & $P(Y=y)$ \
\hline$x_{1}$ & $p_{1}$ & & $g\left(x_{1}\right)$ & $p_{1}$ \
$x_{2}$ & $p_{2}$ & & $g\left(x_{2}\right)$ & $p_{2}$ \
$x_{3}$ & $p_{3}$ & & $g\left(x_{3}\right)$ & $p_{3}$ \
$\vdots$ & $\vdots$ & & $\vdots$ & $\vdots$ \
\hline
\end{表格}
这提出了一种寻找房车 PMF 的策略。使用不熟悉的分布:尝试表达 r.v.作为 r.v. 的一对一功能具有已知分布。下一个示例说明了这种方法。
示例 3.7.2(随机游走)。粒子在数轴上移动 $n$ 步。粒子从 0 开始,在每一步它以相等的概率向右或向左移动 1 个单位。假设所有步骤都是独立的。令$Y$ 为$n$ 步后粒子的位置。求 $Y$ 的 PMF。
解决方案:
将每个步骤视为伯努利试验,其中右侧被视为成功,左侧被视为失败。那么粒子向右走的步数就是$\operatorname{Bin}(n, 1 / 2)$随机变量,我们可以命名为$X$。如果$X=j$,则粒子向右走了$j$步,向左走了$nj$步,最终的位置为$j-(nj)=2 jn。$所以我们可以表示$Y $作为$X$的一对一函数,即$Y=2 Xn$。由于 $X$ 采用 ${0,1,2, \ldots, n} 中的值,因此 Y$ 采用 ${-n, 2-n, 4-n, \ldots, n} 中的值。
然后可以从 $X$ 的 PMF 中找到 $Y$ 的 PMF:
$$
P(Y=k)=P(2 X-n=k)=P(X=(n+k) / 2)=\left(\begin{array}{c}
n \
\frac{n+k}{2}
\end{数组}\right)\left(\frac{1}{2}\right)^{n}
$$
如果$k$ 是$-n$ 和$n$(包括)之间的整数,使得$n+k$ 是偶数。
如果 $g$ 不是一对一的,那么对于给定的 $y$,可能有多个 $x$ 值,使得 $g(x)=y$。计算
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。