统计代写| Linearity of expectation stat代写
统计代考
4.2 Linearity of expectation
The most important property of expectation is linearity: the expected value of a sum of r.v.s is the sum of the individual expected values.
Theorem 4.2.1 (Linearity of expectation). For any r.v.s $X, Y$ and any constant $c$,
$$
\begin{aligned}
E(X+Y) &=E(X)+E(Y) \
E(c X) &=c E(X)
\end{aligned}
$$
The second equation says that we can take out constant factors from an expectation; this is both intuitively reasonable and easily verified from the definition. The first equation, $E(X+Y)=E(X)+E(Y)$, also seems reasonable when $X$ and $Y$ are independent. What may be surprising is that it holds even if $X$ and $Y$ are dependent! To build intuition for this, consider the extreme case where $X$ always equals $Y$. Then $X+Y=2 X$, and both sides of $E(X+Y)=E(X)+E(Y)$ are equal to $2 E(X)$, so linearity still holds even in the most extreme case of dependence.
Linearity is true for all r.v.s, not just discrete r.v.s, but in this chapter we will prove it only for discrete r.v.s. Before proving linearity, it is worthwhile to recall some basic facts about averages. If we have a list of numbers, say $(1,1,1,1,1,3,3,5)$, we can calculate their mean by adding all the values and dividing by the length of the list, so that each element of the list gets a weight of $\frac{1}{8}$ :
$$
\frac{1}{8}(1+1+1+1+1+3+3+5)=2
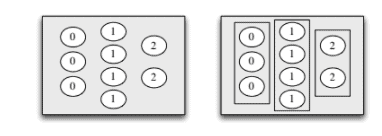
$$ Expectation But another way to calculate the mean is to group together all the 1 ‘s, all the 3 ‘s, and all the 5’s, and then take a weighted average, giving appropriate weights to 1 ‘s, 3 ‘s, and 5’s: $$ 5 $$ This insight-that averages can be calculated in two ways, ungrouped or groupedis all that is needed to prove linearity! Recall that $X$ is a function which assigns a real number to every outcome $s$ in the sample space. The r.v. $X$ may assign the same value to multiple sample outcomes. When this happens, our definition of $P(X=x)$, is the total weight of the constituent pebbles. This grouping process is illustrated in Figure $4.3$ for a hypothetical r.v. taking values in ${0,1,2}$. So our definition of expectation corresponds to the grouped way of taking averages.
统计代考
期望的线性
期望最重要的属性是线性:r.v.s 和的期望值是各个期望值的总和。
定理 4.2.1(期望的线性)。对于任何 r.v.s $X、Y$ 和任何常数 $c$,
$$
\开始{对齐}
E(X+Y) &=E(X)+E(Y) \
E(c X) &=c E(X)
\end{对齐}
$$
第二个等式表示我们可以从期望中取出常数因子;这既直观合理,又易于从定义中验证。第一个方程,$E(X+Y)=E(X)+E(Y)$,当 $X$ 和 $Y$ 独立时也似乎是合理的。令人惊讶的是,即使 $X$ 和 $Y$ 相互依赖,它仍然成立!要对此建立直觉,请考虑 $X$ 始终等于 $Y$ 的极端情况。那么$X+Y=2 X$,并且$E(X+Y)=E(X)+E(Y)$的两边都等于$2 E(X)$,所以线性即使在最依赖的极端情况。
线性对于所有 r.v.s 都是正确的,而不仅仅是离散 r.v.s,但在本章中,我们将仅对离散 r.v.s 证明它。在证明线性之前,有必要回顾一些关于平均值的基本事实。如果我们有一个数字列表,比如 $(1,1,1,1,1,3,3,5)$,我们可以通过将所有值相加并除以列表的长度来计算它们的平均值,这样列表中的每个元素的权重为 $\frac{1}{8}$ :
$$
\frac{1}{8}(1+1+1+1+1+3+3+5)=2
$$ 期望 但是另一种计算平均值的方法是将所有 1 、所有 3 和所有 5 组合在一起,然后取加权平均值,给 1 和 3 赋予适当的权重,和 5 的: $$ 5 $$ 这种洞察力 – 可以通过两种方式计算平均值,未分组或分组是证明线性所需的全部!回想一下,$X$ 是一个函数,它为样本空间中的每个结果 $s$ 分配一个实数。房车$X$ 可以为多个样本结果分配相同的值。当这种情况发生时,我们对 $P(X=x)$ 的定义是组成卵石的总重量。对于假设的 r.v.,此分组过程如图 4.3$ 所示。取 ${0,1,2}$ 中的值。所以我们对期望的定义对应于取平均值的分组方式。
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。