数学代写|Some clarification of terminology数值分析代考代写 - 代考代写：100%准时可靠您的作业代写专家

代写隐藏

1 数学代写|Some clarification of terminology 数值分析代考

数学代写|Some clarification of terminology 数值分析代考

数值分析代写

When discussing the inverse conductivity problem:
$$
\nabla \cdot K \nabla u=0
$$
The constant coefficient problem refers to the problem when $K \equiv 1$.
The variable coefficient problem refers to the
problem when $K=K(x, y)$.
Consider our inverse problem involving the PDE
$$
\nabla \cdot K \nabla u=0 \quad \text { in }(-1,1)^{2}
$$
An observation of the input variable $X$ is a collection of measurements of the Dirichlet to Neumann map
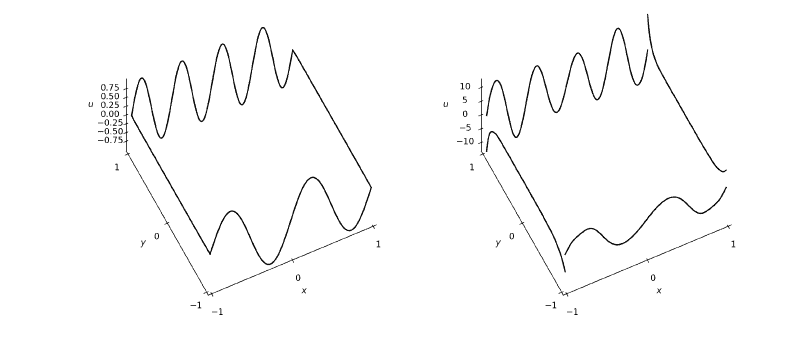
An observation of the output variable $Y$ is a $2 \mathrm{D}$ measurement of the variable coefficient problem
The Dirichlet-to-Neumann map is linear while keeping $K$ fixed
Consider two solutions $u_{1}, u_{2}$ to the conductivity problem
$$
\left{\begin{array} { r l }
{ \nabla \cdot K \nabla u _ { 1 } = 0 } & { \text { in } \Omega } \
{ u _ { 1 } = f _ { 1 } } & { \text { on } \partial \Omega }
\end{array} \left{\begin{array}{rl}
\nabla \cdot K \nabla u_{2}=0 & \text { in } \Omega \
u_{2}=f_{2} & \text { on } \partial \Omega
\end{array}\right.\right.
$$
Then it follows that $u_{3}:=u_{1}+u_{2}$ solves the problem
$$
\left{\begin{aligned}
\nabla \cdot K \nabla u_{3} &=0 \quad \text { in } \Omega \
u_{3} &=f_{1}+f_{2} \quad \text { on } \partial \Omega
\end{aligned}\right.
$$
Thus the Dirichlet-to-Neumann map $\wedge$ satisfies
$$
\Lambda\left(f_{1}+f_{2}\right)=\mathbf{n} \cdot \nabla u_{3}=\mathbf{n} \cdot \nabla u_{1}+\mathbf{n} \cdot \nabla u_{2}=\Lambda\left(f_{1}\right)+\Lambda\left(f_{2}\right) .
$$
In general, consider two solutions $u_{1}, u_{2}$ to the conductivity problem
$$
\left{\begin{array} { r l }
{ \nabla \cdot K _ { 1 } \nabla u _ { 1 } = 0 } & { \text { in } \Omega } \
{ u _ { 1 } = f } & { \text { on } \partial \Omega }
\end{array} \left{\begin{array}{rl}
\nabla \cdot K_{2} \nabla u_{2}=0 & \text { in } \Omega \
u_{2}=f & \text { on } \partial \Omega
\end{array}\right.\right.
$$
However, $u_{3}=u_{1}+u_{2}$ does not satisfy the conductivity equation with the coefficient $K_{1}+K_{2}$.
$$
\begin{aligned}
\nabla \cdot K_{3} \nabla u_{3} &=\nabla \cdot\left(K_{1}+K_{2}\right) \nabla u_{3} \
&=\nabla \cdot K_{1} \nabla u_{3}+\nabla \cdot K_{2} \nabla u_{3}=\nabla \cdot K_{1} \nabla u_{2}+\nabla \cdot K_{2} \nabla u_{1}
\end{aligned}
$$
Thus $\Lambda_{3} \neq \Lambda_{1}+\Lambda_{2}$ in general

数值分析代考

在讨论反电导率问题时：
$$
\nabla \cdot K \nabla u=0
$$
常系数问题是指当$K \equiv 1$ 时的问题。
变系数问题指的是
$K=K(x, y)$ 时的问题。
考虑我们涉及 PDE 的逆问题
$$
\nabla \cdot K \nabla u=0 \quad \text { in }(-1,1)^{2}
$$
对输入变量 $X$ 的观察是 Dirichlet 到 Neumann 映射的测量值的集合
对输出变量 $Y$ 的观察是对变量系数问题的 $2 \mathrm{D}$ 测量
Dirichlet-to-Neumann 映射是线性的，同时保持 $K$ 固定
考虑电导率问题的两个解 $u_{1}, u_{2}$
$$
\left{\begin{array} { r l }
{ \nabla \cdot K \nabla u _ { 1 } = 0 } & { \text { in } \Omega } \
{ u _ { 1 } = f _ { 1 } } & { \text { on } \partial \Omega }
\end{array} \left{\begin{array}{rl}
\nabla \cdot K \nabla u_{2}=0 & \text { in } \Omega \
u_{2}=f_{2} & \text { on } \partial \Omega
\end{数组}\right.\right.
$$
那么 $u_{3}:=u_{1}+u_{2}$ 解决了这个问题
$$
\left{\begin{对齐}
\nabla \cdot K \nabla u_{3} &=0 \quad \text { in } \Omega \
u_{3} &=f_{1}+f_{2} \quad \text { on } \partial \Omega
\end{对齐}\对。
$$
因此 Dirichlet-to-Neumann 映射 $\wedge$ 满足
$$
\Lambda\left(f_{1}+f_{2}\right)=\mathbf{n} \cdot \nabla u_{3}=\mathbf{n} \cdot \nabla u_{1}+\mathbf{n } \cdot \nabla u_{2}=\Lambda\left(f_{1}\right)+\Lambda\left(f_{2}\right) 。
$$
一般来说，考虑两个解决方案 $u_{1}, u_{2}$ 解决电导率问题
$$
\left{\begin{array} { r l }
{ \nabla \cdot K _ { 1 } \nabla u _ { 1 } = 0 } & { \text { in } \Omega } \
{ u _ { 1 } = f } & { \text { on } \partial \Omega }
\end{array} \left{\begin{array}{rl}
\nabla \cdot K_{2} \nabla u_{2}=0 & \text { in } \Omega \
u_{2}=f & \text { on } \partial \Omega
\end{数组}\right.\right.
$$
但是，$u_{3}=u_{1}+u_{2}$ 不满足系数为 $K_{1}+K_{2}$ 的电导方程。
$$
\开始{对齐}
\nabla \cdot K_{3} \nabla u_{3} &=\nabla \cdot\left(K_{1}+K_{2}\right) \nabla u_{3} \
&=\nabla \cdot K_{1} \nabla u_{3}+\nabla \cdot K_{2} \nabla u_{3}=\nabla \cdot K_{1} \nabla u_{2}+\nabla \ cdot K_{2} \nabla u_{1}
\end{对齐}
$$
因此 $\Lambda_{3} \neq \Lambda_{1}+\Lambda_{2}$ 一般