物理代考|Normal Mode Expansion of the Electromagnetic Field 量子力学代写
物理代写
6.6 Normal Mode Expansion of the Electromagnetic Field
The next challenge is to express the free electromagnetic field in normal modes, that is, as a set of uncoupled simple harmonic oscillators. We work in a big cubical box of volume $\Omega=L^{3}$, and apply periodic boundary conditions.
Quantum Electrodynamics
51
The total energy in the free electromagnetic field in the box is obtained through the sum of the squares of the electric and magnetic fields. In SI units it is given by
$$
E=\frac{1}{2} \int_{\Omega} d^{3} x\left(\varepsilon_{0} \vec{E}^{2}+\frac{1}{\mu_{0}} \vec{B}^{2}\right) \quad ; \text { field energy }
$$
One has the freedom of choosing a gauge for the electromagnetic potentials, ${ }^{7}$ and here we work in the Coulomb gauge. This gauge has the great advantage that, when quantized, there is a one-to-one correspondence of the resulting quanta with physical photons. For free fields, the Coulomb gauge is defined by
$\vec{\nabla} \cdot \vec{A}=0 \quad ; \Phi=0 \quad ;$ Coulomb gauge $(6.35)$
The electric and magnetic fields are then given by
$$
\vec{E}=-\frac{\partial \vec{A}}{\partial t} \quad ; \vec{B}=\vec{\nabla} \times \vec{A}
$$
With periodic boundary conditions, the normal modes are given by plane waves
$$
\begin{aligned}
q_{\vec{k}}(\vec{x}, t) &=\frac{1}{\sqrt{\Omega}} e^{i\left(\vec{k} \cdot \vec{x}-\omega_{k} t\right)} & ; \vec{k} &=\frac{2 \pi}{L}\left(n_{x}, n_{y}, n_{z}\right) \
\omega_{k} &=|\vec{k}| c & & ; n_{i}=0, \pm 1, \pm 2, \ldots
\end{aligned}
$$
Once again, we have an infinite, discrete set of wavenumbers, and the nor- mal modes are orthonormal $$ \int_{\Omega} d^{3} x q_{\vec{k}}^{\star}(\vec{x}, t) q_{\vec{k}^{\prime}}(\vec{x}, t)=\delta_{\vec{k}, \vec{k}^{\prime}} $$
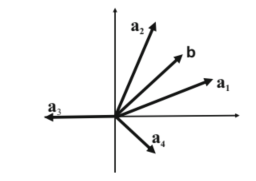
Now introduce a set of orthogonal, transverse unit vectors $\vec{e}$ as shown in Fig. 6.1. They satisfy $\vec{e}{\vec{k} s} \cdot \vec{k}=0$ ${ }{\vec{k} s} \cdot \vec{e}{\vec{k} s^{\prime}}=\delta{s, s^{\prime}}$$; s=1,2$
52
The vector potential can now be expanded in normal modes as follows $\vec{A}(\vec{x}, t)=\sum_{\vec{k}} \sum_{s=1}^{2}\left(\frac{\hbar}{2 \omega_{k} \varepsilon_{0} \Omega}\right)^{1 / 2}\left[a_{\vec{k} s} \vec{e}{\vec{k} s} e^{i\left(\vec{k} \cdot \vec{x}-\omega{k} t\right)}+a_{\vec{k} s}^{\star} \vec{e}{\vec{k} s} e^{-i\left(\vec{k} \cdot \vec{x}-\omega{k} t\right)}\right]$
where we have chosen particular amplitudes for the normal modes which will make the energy come out nicely. This expansion has the following features to recommend it:
- This expression is real, giving rise to real $(\vec{E}, \vec{B}) ;$
- Since only the transverse polarization vectors are used in the expansion, one has ensured that
s.
物理代考
6.6 电磁场的常模扩展
下一个挑战是将正常模式下的自由电磁场表示为一组未耦合的简单谐振子。我们在一个体积 $\Omega=L^{3}$ 的大立方体盒子中工作,并应用周期性边界条件。
量子电动力学
51
盒子内自由电磁场的总能量是通过电场和磁场的平方和得到的。在 SI 单位中,它由下式给出
$$
E=\frac{1}{2} \int_{\Omega} d^{3} x\left(\varepsilon_{0} \vec{E}^{2}+\frac{1}{\mu_{0 }} \vec{B}^{2}\right) \quad ; \text { 场能量 }
$$
可以自由选择电磁势的规范 ${ }^{7}$,这里我们使用库仑规范。该规范具有很大的优势,即在量化时,产生的量子与物理光子一一对应。对于自由场,库仑规范定义为
$\vec{\nabla} \cdot \vec{A}=0 \quad ; \Phi=0 \quad ;$ 库仑规 $(6.35)$
电场和磁场由下式给出
$$
\vec{E}=-\frac{\partial \vec{A}}{\partial t} \quad ; \vec{B}=\vec{\nabla} \times \vec{A}
$$
在周期性边界条件下,正常模式由平面波给出
$$
\开始{对齐}
q_{\vec{k}}(\vec{x}, t) &=\frac{1}{\sqrt{\Omega}} e^{i\left(\vec{k} \cdot \vec{x }-\omega_{k} t\right)} & ; \vec{k} &=\frac{2 \pi}{L}\left(n_{x}, n_{y}, n_{z}\right) \
\omega_{k} &=|\vec{k}| C & & ; n_{i}=0, \pm 1, \pm 2, \ldots
\end{对齐}
$$
再一次,我们有一个无限的离散波数集,并且正常模式是正交 $$ \int_{\Omega} d^{3} x q_{\vec{k}}^{\star}(\ vec{x}, t) q_{\vec{k}^{\prime}}(\vec{x}, t)=\delta_{\vec{k}, \vec{k}^{\prime}} $$
现在引入一组正交的横向单位向量 $\vec{e}$,如图 6.1 所示。它们满足 $\vec{e}{\vec{k} s} \cdot \vec{k}=0$ ${ }{\vec{k} s} \cdot \vec{e}{\vec {k} s^{\prime}}=\delta{s, s^{\prime}}$$; s=1,2$
52
矢量势现在可以在正常模式下展开如下 $\vec{A}(\vec{x}, t)=\sum_{\vec{k}} \sum_{s=1}^{2}\left (\frac{\hbar}{2 \omega_{k} \varepsilon_{0} \Omega}\right)^{1 / 2}\left[a_{\vec{k} s} \vec{e}{ \vec{k} s} e^{i\left(\vec{k} \cdot \vec{x}-\omega{k} t\right)}+a_{\vec{k} s}^{\星} \vec{e}{\vec{k} s} e^{-i\left(\vec{k} \cdot \vec{x}-\omega{k} t\right)}\right] $
我们为正常模式选择了特定的振幅,这将使能量很好地输出。这个扩展有以下特点推荐它:
- 这个表达式是实数,产生实数 $(\vec{E}, \vec{B}) ;$
- 由于在扩展中仅使用横向偏振矢量,因此已确保

物理代考| Classical Optics量子力学代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程