物理代写| Equivalence Principle: Weak Form 相对论代考
物理代写
2.1 Equivalence Principle: Weak Form
The principle of equivalence implies a deep connection between inertia and gravitation.
It is said that Galileo dropped massive objects from heights and observed the fall of the objects. The observation was that different objects made of different materials fell at the same rate within experimental errors and modulo other physical factors affecting the experiment. Even as of today there is no fundamental reason why this should be so. However, todays high precision experiments show within experimental error that this is indeed so. Equivalence principle has been experimentally verified to better than one part in $\sim 10^{14}$ (Touboul et al. (2017)). We make the notions more precise below. It is interesting to note that Galileo was also involved in the founding of the equivalence principle apart from the principle of relativity. In fact these are the two principles that underpin GR.
Let an object be placed in a gravitational field whose acceleration due to gravity is given by $\mathbf{g}$, then the force acting on the object is given by $\mathbf{F}=m_{g} \mathbf{g}$, where $m_{g}$ is the constant of proportionality called the gravitational mass. The quantity $m_{g}$ describes the response of the object to gravity. On the other hand, according to Newton’s second law of motion, the acceleration of a body a is proportional to the force $\mathbf{F}$ applied to it, such that, $\mathbf{F}=m_{i}$ a, where $m_{i}$ is another constant, representing the resistance of the object to motion-the inertia of the body. It is called the inertial mass of the body (the same property that appears in the definition of momentum, kinetic energy etc.). Therefore for a body falling under gravity, one can write the equation:
$$
\mathbf{a}=\left(m_{g} / m_{i}\right) \mathbf{g} .
$$
Galileo’s experiments indicate that the ratio $m_{g} / m_{i}$ should be the same for all bodies. This is taken as a principle in GR called the equivalence principle in its weak form. It is called the weak equivalence principle (WEP). The units can be chosen in such a way that the ratio $m_{g} / m_{i}=1$. Then the weak equivalence principle asserts that $m_{g}=m_{i}$ for all bodies irrespective of their mass or other constituents. Many experiments have been performed to measure the deviation of $m_{g} / m_{i}$ from one, but so far every experiment has produced a null result, that is, $m_{g} / m_{i}$ has come out to be very close to unity, in conformity with the equivalence principle. This makes gravity a special kind of force. The other forces, e.g., electromagnetic forces are proportional to the charge and so produce accelerations depending on the charge to mass ratios which could be different for different objects. But gravity produces the same acceleration on every body, or in other words, the ratio of gravitational charge to its mass (inertial) is the same for all bodies. This is the key property that lends gravity to geometrisation.
It is important to remark that $m_{g}=m_{i}$ is simply a coincidence in Newton’s theory. In physics, it is customary to look upon any such coincidence as suspicious. Einstein’s theory of relativity (GR), far from taking it as a coincidence, takes it as a principle underpinning the theory. If it were found that this equality does not hold true, Newton’s theory of gravity would still stand, but Einstein’s theory would fall. This is in fact a strength of Einstein’s theory.
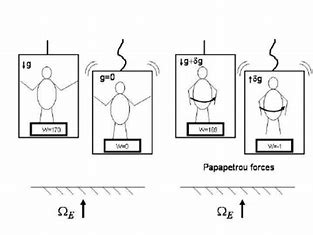
Imagine an observer in a closed elevator. If the elevator is in a gravitational field $\mathbf{g}$, the observer will feel a weight $m_{g} \mathbf{g}$. While if the capsule was far away from every other body (negligible gravitational force) and was subject to an acceleration $-\mathbf{g}$, the observer would feel a weight $m_{i}$ g. Since $m_{g}=m_{i}$, the observer would not be able to distinguish between these two scenarios by feeling his/her weight. By a similar logic, in a freely falling elevator of small dimensions, all masses would fall at the same rate and would remain stationary with respect to each other within the small region. In this “local” region one has then got rid of gravity. It is always possible to get rid of gravity in a sufficiently small region of spacetime. What decides the size of this region? It is the non-uniformity of the gravitational field and the accuracy of the measurements that can be performed. This can be explained by a concrete example. Consider an observer who drops a ball or better two balls in a frame freely falling in the field of the earth. Then they would stay at rest with respect to each other, so the frame would appear to be inertial, at least, for a short time. However, if the balls are observed for a longer time, due to the radial and non-uniform nature of earth’s gravitational field, the balls would slowly move with respect to each other-if the two ball were initially separated vertically, the separation will tend to increase, because the pull on the ball nearer to Earth would be stronger; on the other hand, if the initial separation was horizontal, the separation will tend to decrease, because the balls are falling towards the centre of the Earth-the point is that the observer will be able to measure the non-uniformity of the field by observing the relative motion of the balls. This relative motion is proportional to the separation between the balls and also the observation time. If the local region is small in space and time and hence the spatial separation and the time of observation small, the relative motion will be undetectable for a given accuracy of measurement. More accurate the measurement and more non-uniform the field, smaller should be the local region for the motion to be discernable. See Exercise $2.3 .2$ for detailed analysis of a local inertial frame near the Earth’s surface.
The term “local” in the above paragraph is very important. The region both in space and time should be sufficiently small for the gravity (say measured by the acceleration it causes) to be uniform. In a non-uniform gravitational field and with non-local measurements relative motion between test particles can be detected. The cause of this relative motion is the gradient in the gravitational acceleration or differential acceleration and is called the tidal force-gravity exerts a tidal force. Yes, this is the same force that causes tides in the oceans. This is a differential force which causes elastic strain in matter and falls off as $1 / r^{3}$ for a massive point source. This is why the moon has more effect on ocean tides, not the sun, although the sun’s gravitational attraction on the earth is more than that of the moon.
物理代考
2.1 等价原则:弱形式
等效原理暗示了惯性和万有引力之间的深层联系。
据说伽利略从高处坠落了巨大的物体并观察了物体的下落。观察结果是,由不同材料制成的不同物体在实验误差内以相同的速率下降,并以影响实验的其他物理因素为模。即使在今天,也没有根本原因应该如此。然而,今天的高精度实验表明,在实验误差范围内确实如此。等效原理已通过实验验证优于 $\sim 10^{14}$ 中的一个部分(Touboul et al. (2017))。我们在下面使概念更精确。有趣的是,除了相对性原理之外,伽利略还参与了等效原理的建立。事实上,这是支持 GR 的两个原则。
让一个物体被放置在一个重力场中,其重力加速度由 $\mathbf{g}$ 给出,那么作用在物体上的力由 $\mathbf{F}=m_{g} \mathbf{g 给出}$,其中 $m_{g}$ 是称为引力质量的比例常数。数量 $m_{g}$ 描述了物体对重力的响应。另一方面,根据牛顿第二运动定律,物体 a 的加速度与施加在其上的力 $\mathbf{F}$ 成正比,因此,$\mathbf{F}=m_{i}$ a,其中$m_{i}$是另一个常数,代表物体运动的阻力——物体的惯性。它被称为物体的惯性质量(与动量、动能等定义中出现的相同属性)。因此,对于一个在重力下落下的物体,可以写出方程:
$$
\mathbf{a}=\left(m_{g} / m_{i}\right) \mathbf{g} 。
$$
伽利略的实验表明 $m_{g} / m_{i}$ 的比率对于所有物体应该是相同的。这被视为 GR 中的一个原则,在其弱形式中称为等效原则。它被称为弱等价原则(WEP)。单位可以选择为比率 $m_{g} / m_{i}=1$。然后弱等价原理断言,对于所有物体,无论其质量或其他成分如何,$m_{g}=m_{i}$。已经进行了许多实验来测量 $m_{g} / m_{i}$ 与 1 的偏差,但到目前为止,每个实验都产生了一个空结果,即 $m_{g} / m_{i}$ 有出来非常接近统一,符合等价原则。这使得重力成为一种特殊的力。其他力,例如电磁力,与电荷成正比,因此产生的加速度取决于电荷与质量的比率,这对于不同的物体可能是不同的。但是重力在每个物体上产生相同的加速度,或者换句话说,重力电荷与其质量(惯性)的比率对于所有物体都是相同的。这是将重力赋予几何化的关键属性。
值得注意的是,$m_{g}=m_{i}$ 只是牛顿理论中的一个巧合。在物理学中,习惯上认为任何此类巧合都是可疑的。爱因斯坦的相对论 (GR) 远非将其视为巧合,而是将其视为支撑该理论的原理。如果发现这个等式不成立,牛顿的万有引力理论仍然成立,但爱因斯坦的理论就会失败。这实际上是爱因斯坦理论的一个优势。
想象一个在封闭的电梯中的观察者。如果电梯在引力场 $\mathbf{g}$ 中,观察者会感觉到重量 $m_{g} \mathbf{g}$。如果胶囊远离其他物体(重力可以忽略不计)并且受到加速度 $-\mathbf{g}$,观察者会感觉到重量 $m_{i}$g。由于$m_{g}=m_{i}$,观察者将无法通过感受他/她的重量来区分这两种情况。通过类似的逻辑,在一个自由下落的小尺寸电梯中,所有质量将以相同的速度下落,并在小区域内相对于彼此保持静止。在这个“局部”区域,人们摆脱了重力。在足够小的时空区域内摆脱重力总是可能的。是什么决定了这个区域的大小?它是引力场的不均匀性和可以执行的测量的准确性。这可以通过一个具体的例子来解释。考虑一个观察者,他将一个球或更好的两个球在一个框架中自由落入地球的场中。然后它们将相对于彼此保持静止,因此框架至少在短时间内看起来是惯性的。然而,如果长时间观察球,由于地球引力场的径向和非均匀性质,球会相对于彼此缓慢移动——如果两个球最初垂直分离,分离会趋于增加,因为靠近地球的球的拉力会

物理代考| Classical Optics量子力学代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程