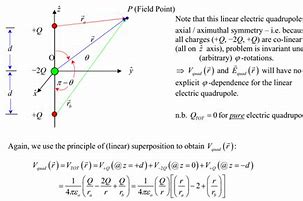
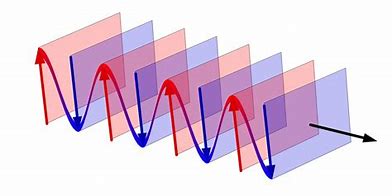
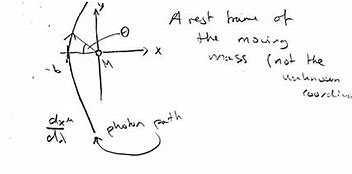
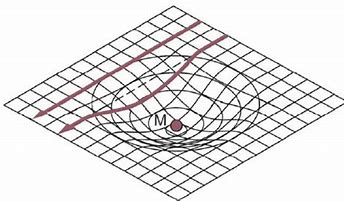
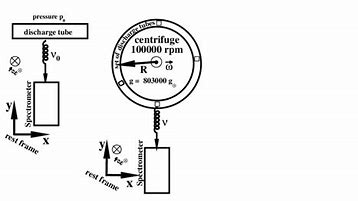
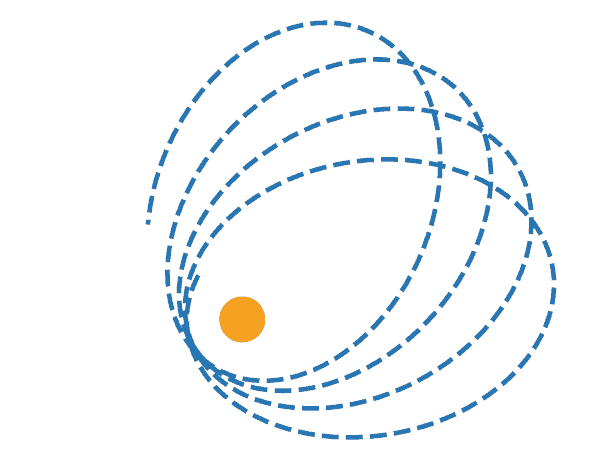
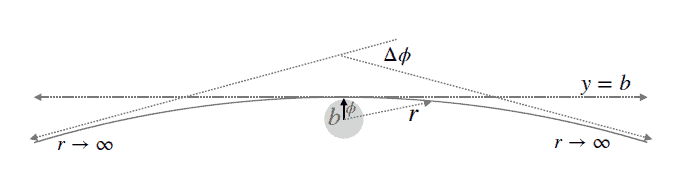
物理代写| Quadrupole Formula 相对论代考 物理代写 we write,$$\bar{h}{k l}(…
Physics 622
Spring 2022
Instructor: Paul Aspinwall
Credits: 1.0, Hours: 3.0
Time: TuTh 10:15AM - 11:30AM
Location: Physics 235
Description
Introduction to the basic concepts and techniques of General Relativity. The course will cover the fundamentals of tensor calculus, Riemannian geometry, and Einstein's equations, as well as applications to cosmology and black holes.
This is a core course for students who want to work in general relativity, cosmology, gravitational lensing, theoretical astrophysics, string theory, or related subjects.
Homework
will be given weekly.
Prerequisites
A sound knowledge of multivariable calculus (at least Math 212) and linear algebra (at least Math 218). A basic knowledge of classical mechanics and electromagnetism is desirable but the course will endevour to be self-contained.
Exams
There might be a mid-term exam. A take-home final will be given due back at the official time of the exam.
Synopsis
A rough outline is as follows.
0. Special Relativity
Minkowski Space
Lorentz Transformations
I. Manifolds and Tensors
Tangent vectors and differentiable maps
Curves, vector fields, and one-forms
Tensor fields and the abstract index notation
II. Riemannian Geometry
Covariant derivatives and parallel transport
Curvature and geodesics
Computing curvature
III. The Einstein Field Equations
General and special covariance
Einstein's equation
The weak-field limit
IV. Applications
Cosmology
Robertson-Walker universes
The cosmological constant (“dark energy”)
The Schwarzschild solution
Gravitational red shift
Black holes
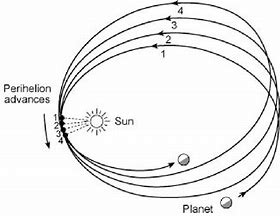
Perihelion precession and bending of light
The Kruskal extension
Gravitational Waves
Emission
Binary pulsar decay
LIGO results
Further Analysis of Black Holes
The Reissner-Nordström Solution
The Kerr Solution
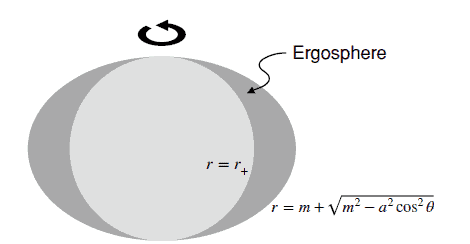
The Ergosphere
Black Hole Thermodynamics
Textbooks
The course will be based on the text:
Robert M. Wald, General Relativity, University of Chicago Press, Chicago, 1984.
See also
Sean M. Carroll, Spacetime and Geometry, An Introduction to General Relativity, Addison Wesley 2004. (See also gr-qc/9712019 for what might be considered to be an earlier form of this book online.)
2022 年春季
教练:保罗·阿斯平沃尔
学分:1.0,小时:3.0
时间:星期二 10:15AM - 11:30AM
地点:物理235
描述
介绍广义相对论的基本概念和技术。本课程将涵盖张量微积分、黎曼几何和爱因斯坦方程的基础知识,以及在宇宙学和黑洞中的应用。
对于想要从事广义相对论、宇宙学、引力透镜、理论天体物理学、弦论或相关学科的学生来说,这是一门核心课程。
在家工作
将每周一次。
先决条件
多变量微积分(至少数学 212)和线性代数(至少数学 218)的良好知识。经典力学和电磁学的基本知识是可取的,但课程将努力做到自成一体。
考试
可能会有期中考试。带回家的期末考试将在考试的正式时间到期。
概要
大致轮廓如下。
0. 狭义相对论
闵可夫斯基空间
洛伦兹变换
一、流形和张量
切向量和可微映射
曲线、向量场和一式
张量场和抽象索引符号
二、黎曼几何
协变导数和并行传输
曲率和测地线
计算曲率
三、爱因斯坦场方程
一般和特殊协方差
爱因斯坦方程
弱场极限
四。应用
宇宙学
罗伯逊-沃克宇宙
宇宙常数(“暗能量”)
史瓦西解决方案
引力红移
黑洞
近日点进动和光的弯曲
克鲁斯卡尔扩展
引力波
排放
双脉冲星衰变
LIGO 结果
黑洞的进一步分析
Reissner-Nordström 解决方案
克尔解决方案
Ergosphere
黑洞热力学
教科书
该课程将基于以下文本:
Robert M. Wald,广义相对论,芝加哥大学出版社,芝加哥,1984 年。
也可以看看
Sean M. Carroll,时空与几何,广义相对论导论,Addison Wesley,2004 年。(另请参阅 gr-qc/9712019,了解这本书的早期在线形式。)
物理代写| PlaneWave Solutions 相对论代考 物理代写 8.4 Plane Wave Solution…
物理代写| Linearised Gravity 相对论代考 物理代写 8.2 Linearised GravityWe…
物理代写| Shapiro Time Delay 相对论代考 物理代写 7.5 Shapiro Time DelayAn…
物理代写| Gravitational Redshift Pound-Rebka Experiment 相对论代考 物理…
物理代写| The Perihelion Shift in the Orbit of Mercury 相对论代考 物理代…
物理代写| The Deflection of Light by a Central Mass 相对论代考 物理代写 7…
物理代写| Kerr Spacetime and the Rotating Black Hole 相对论代考 物理代写 …
物理代写| Orbits in Schwarzschild Spacetime 相对论代考 物理代写 6.4 Orbit…