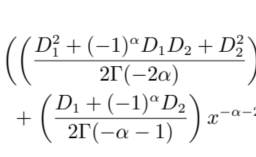物理代写| The Schwarzschild Metric 相对论代考
物理代写
6.3 Event Horizons and Black Holes
In this section we generally describe black holes and then show that the Schwarzschild spacetime where the matter has collapsed beyond $r=2 \mathrm{~m}$. We investigate the solution for all $r>0$ and show that it is a black hole solution. We especially discuss the surface
$6.3$ Event Horizons and Black Holes
103
$r=2 m$ and show that it has special properties. The surface is called the event horizon.
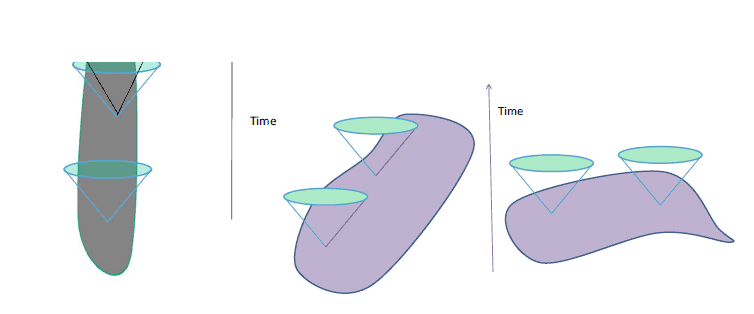
The defining property of the event horizon is its one way nature. It is known generally and popularly that particles, even light cannot escape from a black hole or through the event horizon. Particles from outside the event horizon, in the case of the Schwarzschild black hole the region $r>2 m$, can enter into the region $r<2 m$, but particles inside or on the event horizon cannot escape to the outside or to infinity. Thus the event horizon is a one way membrane for particles with non-zero or zero rest mass. Thus one way membranes have a special role to play when defining event horizons or black holes. We will examine this concept in the simplest situation when the spacetime is flat-that of SR. Clearly here there are no black holes, but one-way membranes exist, but they do not surprise us. Why not? This is the question we will attempt to answer. The discussion below is based on very elegant and intuitive arguments given by C. V. Vishveshwara (Vishveshwara (1968)). The lightcone field in the spacetime is of utmost importance in defining one way membranes and black holes. 6.3.1 One Way Membranes in Special Relativity Let us first look at some examples in SR. The spacetime metric is: $$ d s^{2}=c^{2} d t^{2}-\left(d x^{2}+d y^{2}+d z^{2}\right) . $$ To decide whether a hypersurface-a 3 dimensional subspace of the 4 dimensional spacetime-is a one way membrane, lightcones are of utmost importance-infact they define such a membrane. At any point in the spacetime and more specifically, at each point on the worldline of a particle, we can draw a lightcone. At any point, the tangent to the worldline of the particle, namely, the 4-velocity vector say $u^{i}$, lies inside the future light cone. If the particle has non-zero rest-mass then, $u_{i} u^{i}=1$ and $u^{0}>0$. Such a vector is called timelike and future pointing. All such vectors and their positive scalar multiples consititute the inside of the future lightcone-i.e. $\lambda u^{i}, \quad \lambda>0$ are the vectors constituting the inside of the future lightcone. On the other hand if the particle has zero rest-mass, then $u_{i} u^{i}=0$ and $u^{0}>0$. This vector is future null and lies on the boundary of the future lightcone. Similarly, we have the past lightcone consisting of past timelike and null vectors with $u^{0}<0$-the null vectors essentially forming a boundary to the set of timelike vectors (since here we have made a reference to boundaries which is a topological notion, we mention that, the relevant topology is the usual topology on $\mathcal{R}^{4}$ ). A particle moves from the past lightcone into the future lightcone at any given point on its worldline. Claim: The hypersurface $c t=$ const. is a one-way membrane. Clearly, when a particle has crossed a given time instant it cannot get back to that instant ‘later’ on its worldline. This can be easily ascertained by constructing a lightcone at a given space point say $\left(x_{0}, y_{0}, z_{0}\right)$ on the hypersurface, say, $c t=$ 6.3 Event Horizons and Black Holes In this section we generally describe black holes and then show that the Schwarzschild spacetime where the matter has collapsed beyond $r=2 m$. We investigate the solution for all $r>0$ and show that it is a black hole solution. We especially discuss the surface
$6.3$ Event Horizons and Black Holes
103
$r=2 m$ and show that it has special properties. The surface is called the event horizon.
The defining property of the event horizon is its one way nature. It is known generally and popularly that particles, even light cannot escape from a black hole or through the event horizon. Particles from outside the event horizon, in the case of the Schwarzschild black hole the region $r>2 m$, can enter into the region $r<2 m$, but particles inside or on the event horizon cannot escape to the outside or to infinity. Thus the event horizon is a one way membrane for particles with non-zero or zero rest mass. Thus one way membranes have a special role to play when defining event horizons or black holes. We will examine this concept in the simplest situation when the spacetime is flat-that of SR. Clearly here there are no black holes, but one-way membranes exist, but they do not surprise us. Why not? This is the question we will attempt to answer. The discussion below is based on very elegant and intuitive in the spacetime is of utmost importance in defining one way membranes and black holes. 6.3.1 One Way Membranes in Special Relativity Let us first look at some examples in SR. The spacetime metric is: $$ d s^{2}=c^{2} d t^{2}-\left(d x^{2}+d y^{2}+d z^{2}\right) . $$ To decide whether a hypersurface-a 3 dimensional subspace of the 4 dimensional spacetime-is a one way membrane, lightcones are of utmost importance-infact they define such a membrane. At any point in the spacetime and more specifically, at each point on the worldline of a particle, we can draw a lightcone. At any point, the tangent to the worldline of the particle, namely, the 4-velocity vector say $u^{i}$, lies inside the future light cone. If the particle has non-zero rest-mass then, $u_{i} u^{i}=1$ and $u^{0}>0$. Such a vector is called timelike and future pointing. All such vectors and their positive scalar multiples consititute the inside of the future lightcone-i.e. $\lambda u^{i}, \lambda>0$ are the vectors constituting the inside of the future lightcone. On the other hand if the particle has zero rest-mass, then $u_{i} u^{i}=0$ and $u^{0}>0$. This vector is future null and lies on the boundary of the future lightcone. Similarly, we have the past lightcone consisting of past timelike and null vectors with $u^{0}<0$-the null vectors essentially forming a boundary to the set of timelike vectors (since here we have made a reference to boundaries which is a topological notion, we mention that, the relevant topology is the usual topology on $\mathcal{R}^{4}$ ). A particle moves from the past lightcone into the future lightcone at any given point on its worldline.
Claim: The hypersurface $c t=\mathrm{const}$. is a one-way membrane.
Clearly, when a particle has crossed a given time instant it cannot get back to that instant ‘later’ on its worldline. This can be easily ascertained by constructing a lightcone at a given space point say $\left(x_{0}, y_{0}, z_{0}\right)$ on the hypersurface, say, $c t=$
物理代考
6.3 事件视界和黑洞
在本节中,我们一般描述黑洞,然后展示物质坍缩超过 $r=2 \mathrm{~m}$ 的施瓦西时空。我们研究了所有 $r>0$ 的解决方案,并证明它是一个黑洞解决方案。我们特别讨论表面
$6.3$ 事件视界和黑洞
103
$r=2 m$ 并表明它具有特殊性质。该表面称为事件视界。
事件视界的定义属性是其单向性。众所周知,粒子,甚至光都无法从黑洞或事件视界中逃脱。来自事件视界外的粒子,在史瓦西黑洞 $r>2 m$ 区域的情况下,可以进入 $r<2m$ 区域,但事件视界内部或事件视界上的粒子无法逃逸到外部或到无穷远。因此,事件视界是非零或零静止质量粒子的单向膜。因此,膜在定义事件视界或黑洞时发挥了特殊作用。我们将在最简单的情况下研究这个概念,即时空与 SR 的时空平坦。显然这里没有黑洞,但存在单向膜,但它们并不让我们感到惊讶。为什么不?这是我们将试图回答的问题。下面的讨论基于 C. V. Vishveshwara (Vishveshwara (1968)) 给出的非常优雅和直观的论点。时空中的光锥场对于定义单向膜和黑洞至关重要。 6.3.1 狭义相对论中的单向膜 让我们首先看一些 SR 中的例子。时空度量为: $$ d s^{2}=c^{2} d t^{2}-\left(d x^{2}+d y^{2}+d z^{2}\right) 。 $$ 为了确定超表面(4 维时空的 3 维子空间)是否是单向膜,光锥至关重要——事实上,它们定义了这样的膜。在时空中的任何一点,更具体地说,在粒子世界线上的每一点,我们都可以画出一个光锥。在任何一点,粒子世界线的切线,即 4 速度向量 $u^{i}$,都位于未来光锥内。如果粒子具有非零静止质量,则 $u_{i} u^{i}=1$ 且 $u^{0}>0$。这样的向量称为类时间和未来指向。所有这些向量及其正标量倍数构成了未来光锥的内部——即$\lambda u^{i}, \quad \lambda>0$ 是构成未来光锥内部的向量。另一方面,如果粒子的静止质量为零,则 $u_{i} u^{i}=0$ 且 $u^{0}>0$。这个向量是future null 并且位于future lightcone 的边界上。类似地,我们有过去的光锥,由过去的类时向量和空向量组成,$u^{0}<0$-空向量基本上形成了类时向量集的边界(因为这里我们已经引用了边界,即一个拓扑概念,我们提到,相关拓扑是 $\mathcal{R}^{4}$ 上的常见拓扑。一个粒子在其世界线上的任何给定点从过去的光锥移动到未来的光锥。 声明:超曲面 $c t=$ const。是一种单向膜。 很明显,当一个粒子穿过一个给定的时间瞬间时,它不能在其世界线上“稍后”回到那个瞬间。这可以通过在超曲面上的给定空间点 $\left(x_{0}, y_{0}, z_{0}\right)$ 上构造一个光锥来轻松确定,例如 $c t=$ 6.3 事件视界和黑洞 在本节中,我们一般描述黑洞,然后展示物质塌缩超过 $r=2 m$ 的施瓦西时空。我们研究了所有 $r>0$ 的解决方案,并证明它是一个黑洞解决方案。我们特别讨论表面
$6.3$ 事件视界和黑洞
103
$r=2 m$ 并表明它具有特殊性质。该表面称为事件视界。
事件视界的定义属性是其单向性。众所周知,粒子,甚至光都无法从黑洞或事件视界中逃脱。来自事件视界外的粒子,在史瓦西黑洞 $r>2 m$ 区域的情况下,可以进入 $r<2m$ 区域,但事件视界内部或事件视界上的粒子无法逃逸到外部或到无穷远。因此,事件视界是非零或零静止质量粒子的单向膜。因此,膜在定义事件视界或黑洞时发挥了特殊作用。我们将在最简单的情况下研究这个概念,即时空与 SR 的时空平坦。显然这里没有黑洞,但存在单向膜,但它们并不让我们感到惊讶。为什么不?这是我们将试图回答的问题。下面的讨论基于非常优雅和直观的时空对于定义单向膜和黑洞至关重要。
6.3.1 狭义相对论中的单向膜
让我们首先看一些 SR 中的例子。时空度量为:
$$
d s^{2}=c^{2} d

物理代考Gravity and Curvature of Space-Time 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程