数学代写代考| Time Value of Money and Annuities 离散数学代写 - 代考代写：100%准时可靠您的作业代写专家

The time value of money discusses the concept that the earlier that cash is received the greater value it has to the recipient. Similarly, the later that a cash payment is made, the lower its value to the recipient, and the lower its cost to the payer.
This is clear if we consider the example of a person who receives $\$ 1000$ now and a person who receives $\$ 10005$ years from now. The person who receives $\$ 1000$ now is able to invest it and to receive annual interest on the principal, whereas the other person who rpecives $\$ 1000$ in 5 years earns no interest during the period. Further, the inflation during the period means that the purchasing power of $\$ 1000$ is less in 5 years time is less than it is today.

We presented the general formula for what the future value of a principal $P$ invested for $n$ years at a compound rate $r$ of interest is $A=P(1+r)^{n}$. We can determine the present value of an amount $A$ received in $n$ years time at a discount rate $r$ by
$$
P=\frac{A}{(1+r)^{n}}
$$
5.6 Time Value of Money and Annuities
95
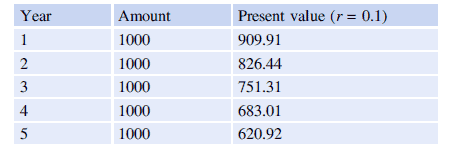
An annuity is a series of equal cash payments made at regular intervals over a period of time, and so there is a need to calculate the present value of the series of payments made over the period. The actual method of calculation is clear from Table $5.2$.
Example (Annuities)
Calculate the present value of a series of payments of $\$ 1000$ (made at the end of each year) with the payments made for 5 years at a discount rate of $10 \%$.
Solution
The regular payment $A$ is 1000 , the rate $r$ is $0.1$ and $n=5$. The present value of the payment received at the end of year 1 is $1000 / 1.1=909.91$; at the end of year 2 it is $1000 /(1.1)^{2}=826.45$; and so on. The total present value of the payments over the 5 years is given by the sum of the individual present values and is $\$ 3791$ (Table $5.2$ ).
We may easily derive a formula for the present value of a series of payments $A$ over a period of $n$ years at a discount rate of $r$ as follows: Clearly, the present value is given by
$$
\frac{A}{(1+r)}+\frac{A}{(1+r)^{2}}+\cdots+\frac{A}{(1+r)^{n}}
$$
This is a geometric series where the constant ratio is $\frac{1}{1+r}$ and the present value of the annuity is given by its sum:
$$
\mathrm{PV}=\frac{A}{r}\left[1-\frac{1}{(1+r)^{n}}\right]
$$
For the example above, we apply the formula and get
$$
\begin{aligned}
\mathrm{PV} &=\frac{1000}{0.1}\left[1-\frac{1}{(1.1)^{5}}\right] \
&=10000(0.3791) \
&=\$ 3791
\end{aligned}
$$
Financial mathematics is discussed in more detail in Chap. $25 .$
\begin{tabular}{|l|l|l|l|}
\hline Table $5.2$ Calculation of present value of annuity & Year & Amount & Present value $(r=0.1)$ \
\hline
\end{tabular}

货币时间价值讨论了越早收到现金对收款人的价值越大的概念。同样，现金支付的时间越晚，对收款人的价值就越低，对付款人的成本也就越低。
如果我们考虑一个人现在收到 $\$ 1000$ 和一个人从现在收到 $\$ 10005$ 的例子，这一点就很清楚了。现在收到 $\$1000$ 的人能够投资它并获得本金的年度利息，而另一个在 5 年内收到 $\$1000$ 的人在此期间没有任何利息。此外，这一时期的通货膨胀意味着 1000 美元的购买力在 5 年内低于今天。

我们提出了一个通用公式，即本金 $P$ 在 $n$ 年内以复合利率 $r$ 的利息投资的未来价值为 $A=P(1+r)^{n}$。我们可以通过以下方式确定在 $n$ 年内以折现率 $r$ 收到的金额 $A$ 的现值
$$
P=\frac{A}{(1+r)^{n}}
$$
5.6 货币和年金的时间价值
95
年金是在一段时间内定期支付的一系列等额现金支付，因此需要计算该期间支付的一系列支付的现值。从表 $5.2$ 中可以清楚地看出实际的计算方法。
示例（年金）
计算一系列付款 $\$1000$（在每年年底进行）的现值，付款期限为 5 年，贴现率为 $10\%$。
解决方案
定期付款 $A$ 是 1000 ，费率 $r$ 是 $0.1$ 和 $n=5$。第 1 年年底收到的付款的现值为 $1000 / 1.1=909.91$；在第 2 年年底是 $1000 /(1.1)^{2}=826.45$;等等。 5 年内付款的总现值由各个现值的总和给出，为 $\$ 3791$（表 $5.2$）。
我们可以很容易地推导出以 $r$ 贴现率在 $n$ 年期间一系列支付 $A$ 的现值的公式，如下所示：显然，现值由下式给出
$$
\frac{A}{(1+r)}+\frac{A}{(1+r)^{2}}+\cdots+\frac{A}{(1+r)^{n}}
$$
这是一个几何级数，其中常数比率为 $\frac{1}{1+r}$，年金的现值由其总和给出：
$$
\mathrm{PV}=\frac{A}{r}\left[1-\frac{1}{(1+r)^{n}}\right]
$$
对于上面的例子，我们应用公式并得到
$$
\开始{对齐}
\mathrm{PV} &=\frac{1000}{0.1}\left[1-\frac{1}{(1.1)^{5}}\right] \
&=10000(0.3791) \
&=\$ 3791
\end{对齐}
$$
金融数学在第 1 章中有更详细的讨论。 25 美元。
\begin{表格}{|l|l|l|l|}
\hline Table $5.2$ 年金现值&年份&金额&现值计算$(r=0.1)$\
\hline
\end{表格}

图论代考

数学中使用的一些函数（或对象）（例如斐波那契数列）是
难以明确定义，最好由递归关系定义：即
递归定义一系列值的方程，一旦一个或多个初始值
值被定义。递归可用于定义函数、序列和
套。
递归定义有两个部分，即基本情况和
递归（归纳）步骤。基本情况通常定义函数的值
$n=0$ 或 $n=1$，而递归步骤指定如何应用
一个数的函数可以从其应用到一个或多个更小的函数中获得
数字。重要的是要注意递归定义，以确保它
不是循环的，也不会导致无限回归。函数的参数
递归步骤中定义的右侧通常小于
左侧的参数以确保终止（有一些不寻常的
递归定义的函数，例如 McCarthy 91 函数，其中 this 不是
案子）。当出现递归定义时，很自然地会问它是否意味着
任何东西，在某些情况下答案是否定的。不动点理论
为递归提供数学基础，并确保
功能/对象定义明确。
第 12 章（第 12.6 节）讨论了各种数学结构，例如偏
阶、完全偏阶和格，可用于给出
为递归奠定坚实的基础。给出了精确的数学含义
根据域和不动点理论递归定义的函数，它是
重要的是可以使用递归的条件
更多详细信息请参阅 [1]。
递归定义将包括至少一个非递归分支，每个递归分支都发生在与原始分支不同的上下文中，并带来
它更接近非递归情况。递归定义是一种强大而优雅的
给出语言结构的指称语义的方法。
接下来，我们给出阶乘函数 $\mathrm{~ N e x t i v i n g ~ d e n t i o n t}$ 的递归定义的例子
和斐波那契数。
例 4.4（函数的递归定义）阶乘函数 $n !$ 非常
在数学中很常见，其著名的定义是 $n !=$
$n(n-1)(n-2) \ldots 3.2 .1$ 和 $0 !=1$。根据基本情况的正式定义
归纳步骤如下：
$\begin{array}{ll}\text { 基本步骤 } & \text { fac }(0)=1 \ \text { 递归步骤 } & \text { fac }(n)=n * \operatorname{fac }(n-1)\end{数组}$
数学中使用的一些函数（或对象）（例如斐波那契数列）是
难以明确定义，最好由递归关系定义：即
递归定义一系列值的方程，一旦一个或多个初始值
值被定义。递归可用于定义函数、序列和
套。
递归定义有两个部分，即基本情况和
递归（归纳）步骤。基本情况通常定义函数的值
$n=0$ 或 $n=1$，而递归步骤指定如何应用
一个数的函数可以从其应用到一个或多个更小的函数中获得
数字。
重要的是要注意递归定义，以确保它
不是循环的，也不会导致无限回归。函数的参数
递归步骤中定义的右侧通常小于
左侧的参数以确保终止（有一些不寻常的
递归定义的函数，例如 $M c$ Carthy 91 函数，其中 this 不是
案子）。
当出现递归定义时，很自然地会问它是否意味着
任何东西，在某些情况下答案是否定的。不动点理论
为递归提供数学基础，并确保
功能/对象定义明确。
第 12 章（Sect. $12.6$）讨论了各种数学结构，例如偏
阶、完全偏阶和格，可用于给出
为递归奠定坚实的基础。给出了精确的数学含义
根据域和不动点理论递归定义的函数，它是
理解可以安全使用递归的条件至关重要。
$\mathrm{~ T h e ~ r e a d e r ~ i s ~ r e f e r}$
这个递归定义定义了一个数字的阶乘的过程
由基本情况确定，或由数字乘以的阶乘确定

数学代写| DISCRETE MATHEMATICS代考请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

Cryptosystem
A system that describes how to encrypt or decrypt messages
Plaintext
Message in its original form
Ciphertext
Message in its encrypted form
Cryptographer
Invents encryption algorithms
Cryptanalyst
Breaks encryption algorithms or implementations

编码理论代写

编码理论（英语：Coding theory）是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错，最近也用于网络编码中。不同学科（如信息论、电机工程学、数学、语言学以及计算机科学）都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正（或检测）数据传输中的错误。

编码共分四类：^[1]