数学代写| Lattices and Order 离散代考
离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式方法, 语言理论, 可计算性, 人工智能, 理论 数据库和软件的可靠性。 离散数学的重点是理论和应用,而不是为了数学本身而研究数学。 一切算法的基础都是离散数学一切加密的理论基础都是离散数学
编程时候很多奇怪的小技巧(特别是所有和位计算相关的东西)核心也是离散数学
其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
离散数学代写
This section considers some the mathematical structures used in the definition of the semantic domains used in denotational semantics. These mathematical structures may also be employed to give a secure foundation for recursion (discussed in Chap. 4), and it is essential that the conditions in which recursion may be used safely be understood.
It is natural to ask when presented with a recursive definition whether it means anything at all, and in some cases the answer is negative. Recursive definitions are a powerful and elegant way of giving the denotational semantics of language constructs. The mathematical structures considered in this section include partial orders, total orders, lattices, complete lattices and complete partial orders.
12.6.1 Partially Ordered Sets
A partial order $\leq$ on a set $P$ is a binary relation such that for all $x, y, z \in P$ the following properties hold:
(i) $x \leq x$ (Reflexivity)
(ii) $x \leq y$ and $y \leq x \quad \Rightarrow x=y$ (Anti-symmetry)
(iii) $x \leq y$ and $y \leq z \Rightarrow x \leq z$ (Transitivity)
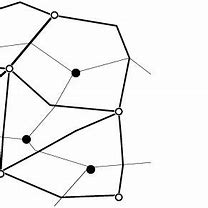
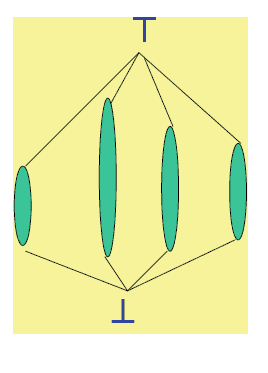
A set $P$ with an order relation $\leq$ is said to be a partially ordered set (Fig. 12.5): Example 12.4 Consider the power set $\mathbb{P} X$, which consists of all the subsets of the set $X$ with the ordering defined by set inclusion. That is, $A \leq B$ if and only if $A \subset B$ set $X$ with the ordering defined by then $\subseteq$ is a partial order on $\mathbb{P} X$.
\begin{tabular}{l} 206 \ \hline Fig. $12.5$ Pictorial represenation of a partial order \end{tabular}
12 Language Theory and Semantics
Order Embedding
A mapping $\phi: P \rightarrow Q$ is said to be an order embedding if.
$x \leq y$ in $P$ if and only if $\phi(x) \leq \phi(y)$ in $Q .$
Order Isomorphism
The mapping $\phi: P \rightarrow Q$ is an order isomorphism if and only if it is an order embedding mapping onto $Q$.
Dual of a Partially Ordered Set
The dual of a partially ordered set $P$ (denoted $P^{\partial}$ ) is a new partially ordered set formed from $P$ where $x \leq y$ holds in $P^{\partial}$ if and only if $y \leq x$ holds in $P$ (i.e. $P^{\partial}$ is obtained by reversing the order on $P$ ).
For each statement about $P$ there is a corresponding statement about $P^{\partial}$. Given any statement $\Phi$ about a partially ordered set, then the dual statement $\Phi^{\partial}$ is obtained by replacing each occurrence of $\leq$ by $\geq$ and vice versa.
Duality Principle
Given that statement $\Phi$ is true of a partially ordered set $P$, then the statement $\Phi^{\partial}$ is true of $P^{\partial}$.
$12.6$ Lattices and Order Maximal and Minimum Elements
207
Let $P$ be a partially ordered set and let $Q \subseteq P$ then (i) $a \in Q$ is a maximal element of $Q$ if $a \leq x \in Q \Rightarrow a=x$
(ii) $a \in Q$ is the greatest (or maximum) element of $Q$ if $a \geq x$ for every $x \in Q$, and in that case we write $a=\max Q$.
A minimal element of $Q$ and the least (or minimum) are defined dually by reversing the order. The greatest element (if it exists) is called the top element and is denoted by $T$. The least element (if it exists) is called the bottom element and is denoted by $\perp$.
Example 12.5 Let $X$ be a set and consider $\mathbb{P} X$ the set of all subsets of $X$ with the ordering defined by set inclusion. The top element $T$ is given by $X$, and the bottom element $\perp$ is given by $\emptyset$.
A finite totally ordered set always has top and bottom elements, but an infinite chain need not have.
图论代考
本节考虑在指称语义中使用的语义域定义中使用的一些数学结构。这些数学结构也可以用来为递归提供一个安全的基础(在第 4 章中讨论),并且必须理解可以安全地使用递归的条件。
当遇到递归定义时,很自然地会问它是否意味着什么,在某些情况下答案是否定的。递归定义是给出语言结构的指称语义的一种强大而优雅的方式。本节考虑的数学结构包括偏序、全序、格、完全格和完全偏序。
12.6.1 偏序集
集合 $P$ 上的偏序 $\leq$ 是二元关系,使得对于所有 $x, y, z \in P$,以下属性成立:
(i) $x \leq x$ (反身性)
(ii) $x \leq y$ 和 $y \leq x \quad \Rightarrow x=y$(反对称)
(iii) $x \leq y$ 和 $y \leq z \Rightarrow x \leq z$ (传递性)
具有顺序关系 $\leq$ 的集合 $P$ 称为偏序集(图 12.5): 例 12.4 考虑幂集 $\mathbb{P} X$,它由使用集合包含定义的顺序设置 $X$。也就是说,$A \leq B$ 当且仅当 $A \subset B$ 设置 $X$ 具有由 then 定义的顺序 $\subseteq$ 是 $\mathbb{P} X$ 上的偏序。
\begin{tabular}{l} 206 \ \hline Fig. $12.5$ 偏序的图形表示 \end{tabular}
12 语言理论和语义学
订单嵌入
一个映射 $\phi: P \rightarrow Q$ 被称为是一个 order embedding if。
$x \leq y$ in $P$ 当且仅当 $\phi(x) \leq \phi(y)$ in $Q .$
阶同构
映射 $\phi: P \rightarrow Q$ 是阶同构当且仅当它是到 $Q$ 的阶嵌入映射。
偏序集的对偶
部分有序集合 $P$ 的对偶(记为 $P^{\partial}$ )是由 $P$ 形成的一个新的部分有序集合,其中 $x \leq y$ 在 $P^{\partial}$ 中成立,如果并且仅当 $y \leq x$ 在 $P$ 中成立(即 $P^{\partial}$ 是通过反转 $P$ 上的顺序获得的)。
对于每个关于 $P$ 的陈述,都有一个关于 $P^{\partial}$ 的相应陈述。给定关于偏序集的任何语句 $\Phi$,则通过将每个出现的 $\leq$ 替换为 $\geq$ 来获得对偶语句 $\Phi^{\partial}$,反之亦然。
对偶原理
鉴于陈述 $\Phi$ 对偏序集 $P$ 为真,那么陈述 $\Phi^{\partial}$ 对 $P^{\partial}$ 为真。
$12.6$ 格和最大和最小元素的阶数
207
令 $P$ 是一个偏序集,令 $Q \subseteq P$ 则 (i) $a \in Q$ 是 $Q$ 的最大元素 if $a \leq x \in Q \Rightarrow a=x$
(ii) $a \in Q$ 是 $Q$ 的最大(或最大)元素,如果对于每个 $x \in Q$ 都有 $a \geq x$,那么我们写成 $a=\max Q$ .
$Q$ 的最小元素和最小(或最小值)通过颠倒顺序来双重定义。最大元素(如果存在)称为顶部元素,用 $T$ 表示。最小元素(如果存在)称为底部元素,用 $\perp$ 表示。
例 12.5 令 $X$ 是一个集合并考虑 $\mathbb{P} X$ 是 $X$ 的所有子集的集合,其顺序由集合包含定义。顶部元素 $T$ 由 $X$ 给出,底部元素 $\perp$ 由 $\emptyset$ 给出。
一个有限的全序集总是有顶元素和底元素,但无限链不一定有。

数学代写| DISCRETE MATHEMATICS代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
抽象代数代考
抽象代数就是一门概念繁杂的学科,我们最重要的一点我想并不是掌握多少例子。即便是数学工作者也不会刻意记住Jacobson环、正则环这类东西,重要的是你要知道这门学科的基本工具和基本手法,对概念理解了没有,而这一点不需要用例子来验证,只需要看看你的理解和后续概念是否相容即可。
矩阵论代考matrix theory
数学,矩阵理论是一门研究矩阵在数学上的应用的科目。矩阵理论本来是线性代数的一个小分支,但其后由于陆续在图论、代数、组合数学和统计上得到应用,渐渐发展成为一门独立的学科。
密码学代考
密码学是研究编制密码和破译密码的技术科学。 研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。 电报最早是由美国的摩尔斯在1844年发明的,故也被叫做摩尔斯电码。
- Cryptosystem
- A system that describes how to encrypt or decrypt messages
- Plaintext
- Message in its original form
- Ciphertext
- Message in its encrypted form
- Cryptographer
- Invents encryption algorithms
- Cryptanalyst
- Breaks encryption algorithms or implementations
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。