数学代考| Syllogistic Logic 离散数学代写代写 - 代考代写：100%准时可靠您的作业代写专家

Early work on logic was done by Aristotle in the fourth century B.C. in the Organon [1]. Aristotle regarded logic as a useful tool of enquiry into any subject, and he developed syllogistic logic. This is a form of reasoning in which a conclusion is drawn from two premises, where each premise is in a subject-predicate form. A common or middle term is present in each of the two premises but not in the conclusion. For example
All Greeks are mortal.
Socrates is a Greek
Therefore Socrates is mortal
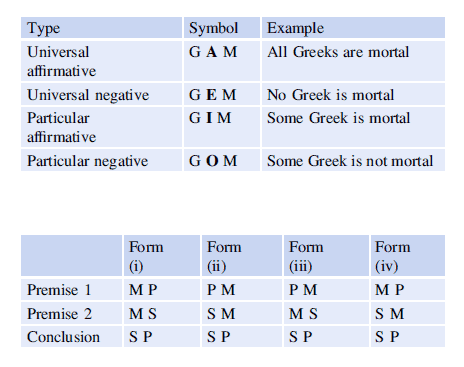
The common (or middle) term in this example is ‘Greek’. It occurs in both premises but not in the conclusion. The above argument is valid, and Aristotle studied and classified the various types of syllogistic arguments to determine those that were valid or invalid. Each premise contains a subject and a predicate, and the middle term may act as a subject or a predicate. Each premise is a positive or negative affirmation, and an affirmation may be universal or particular. The universal and particular affirmations and negatives are described in the table below (Table 14.1)
\begin{tabular}{l|l|l|l|l|}
\hline \multicolumn{1}{l}{$14.2$ Syllogistic Logic } & \multicolumn{1}{l}{227} \
\hline Table 14.1 Types of syllogistic premises & Type & Universal affirmative & G A M & All Greeks are mortal \
\hline Universal negative & G E M & No Greek is mortal \
\hline Particular affirmative & Particular negative & G O M & Some Greek is mortal \
\hline Table 14.2 Forms of syllogistic premises & Some Greek is not mortal \
\hline
\end{tabular}
This leads to four basic forms of syllogistic arguments (Table 14.2), where the middle is the subject of both premises; the predicate of both premises; and the subject of one premise and the predicate of the other premise.
This leads to fo the subjectic is of one premises
\begin{tabular}{l|l|l|l|l|}
\hline & Form (i) & Form (ii) & Form (iii) & Form (iv) \
\hline Premise 1 & M P & P M & P M & M P \
\hline Premise 2 & M S & S M & M S & S M \
\hline Conclusion & S P & S P & S P & S P \
\hline
\end{tabular}$} \
{\text { both premises; the predicate of both premises; and the }} \
{\text { d the predicate of the other premise. }} \
{\text { premises (A, E, I and O), and therefore, sixteen sets of }} \end{array}$

图论代考

早期的逻辑工作是由亚里士多德在公元前四世纪完成的。在欧加农 [1]。亚里士多德认为逻辑是探究任何主题的有用工具，他发展了三段论逻辑。这是一种推理形式，其中从两个前提得出结论，其中每个前提都采用主谓形式。两个前提中的每一个都有一个共同的或中间项，但结论中没有。例如
所有的希腊人都会死。
苏格拉底是希腊人
所以苏格拉底是必死的
此示例中的常用（或中间）术语是“希腊语”。它出现在两个前提中，但不在结论中。上述论证是有效的，亚里士多德对各种三段论论证进行了研究和分类，以确定哪些是有效的，哪些是无效的。每个前提都包含一个主语和一个谓语，而中项可以充当主语或谓语。每个前提都是肯定的或否定的肯定，肯定可以是普遍的或特殊的。下表描述了普遍和特殊的肯定和否定（表 14.1）
\begin{表格}{l|l|l|l|l|}
\hline \multicolumn{1}{l}{$14.2$ 三段论逻辑} & \multicolumn{1}{l}{227} \
\hline 表 14.1 三段论前提的类型 & 类型 & 全称肯定 & G A M & 所有希腊人都是会死的 \
\hline 普遍否定 & G E M & No Greek is mortal \
\hline 特别肯定 & 特别否定 & G O M & Some Greek is mortal \
\hline 表 14.2 三段论前提的形式 & 一些希腊语不是会死的 \
\hline
\end{表格}
这导致了四种基本形式的三段论论证（表 14.2），其中中间是两个前提的主语；两个前提的谓词；以及一个前提的主语和另一个前提的谓语。
这导致主题是一个前提
\begin{表格}{l|l|l|l|l|}
\hline & 表格 (i) & 表格 (ii) & 表格 (iii) & 表格 (iv) \
\hline 前提 1 & M P & P M & P M & M P \
\hline 前提 2 & M S & S M & M S & S M \
\hline 结论 & S P & S P & S P & S P \
\hline
\end{表格}$} \
{\text { 两个前提；两个前提的谓词；和 }} \
{\text { d 另一个前提的谓词。 }} \
{\text { 前提（A、E、I 和 O），因此，十六组 }} \end{array}$

数学代写| DISCRETE MATHEMATICS代考请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

Cryptosystem
A system that describes how to encrypt or decrypt messages
Plaintext
Message in its original form
Ciphertext
Message in its encrypted form
Cryptographer
Invents encryption algorithms
Cryptanalyst
Breaks encryption algorithms or implementations

编码理论代写

编码理论（英语：Coding theory）是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错，最近也用于网络编码中。不同学科（如信息论、电机工程学、数学、语言学以及计算机科学）都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正（或检测）数据传输中的错误。

编码共分四类：^[1]