数学代考| Truth Tables 离散数学代写代写 - 代考代写：100%准时可靠您的作业代写专家

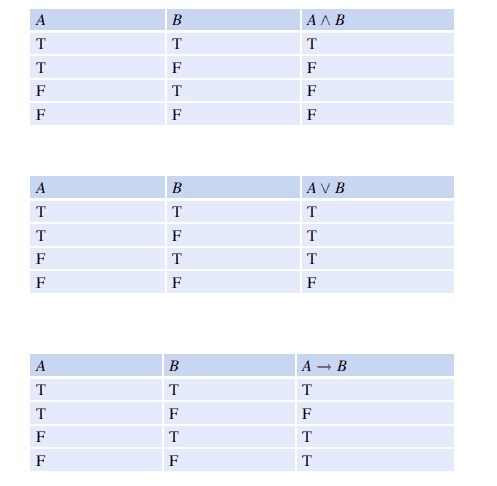
Truth tables give operational definitions of the most important logical connectives, and they provide a mechanism to determine the truth-values of more complicated compound expressions. Compound expressions are formed from propositions and connectives, and the truth-values of a compound expression containing several propositional variables are determined from the underlying propositional variables and the logical connectives.

The conjunction of $A$ and $B$ (denoted $A \wedge B$ ) is true if and only if both $A$ and $B$ are true, and is false in all other cases (Table 15.2). The disjunction of two propositions $\mathrm{A}$ and $\mathrm{B}$ (denoted $A \vee B$ ) is true if at least one of $A$ and $B$ are true, and false in all other cases (Table 15.3). The disjunction operator is known as the ‘inclusive or’ operator as it is also true when both $A$ and $B$ are true; there is also an exclusive or operator that is true exactly when one of $A$ or $B$ is true and is false otherwise.
Example 15.1 Consider proposition A given by “An orange is a fruit” and proposition B given by ‘ $2+2=5$ ‘, then $A$ is true and $B$ is false. Therefore
(i) $A \wedge B$ (i.e. An orange is a fruit and $2+2=5$ ) is false,
(ii) $A \vee B$ (i.e. An orange is a fruit or $2+2=5$ ) is true.

There are many well-known properties of propositional calculus such as the commutative, associative and distributive properties. These ease the evaluation of complex expressions and allow logical expressions to be simplified.

The commutative property holds for the conjunction and disjunction operators, and it states that the order of evaluation of the two propositions may be reversed without affecting the resulting truth-value, i.e.
$$
\begin{aligned}
&A \wedge B=B \wedge A \
&A \vee B=B \vee A
\end{aligned}
$$
The associative property holds for the conjunction and disjunction operators. This means that the order of evaluation of a sub-expression does not affect the resulting truth-value, i.e.
246
15 Propositional and Predicate Logic
$$
\begin{aligned}
&(A \wedge B) \wedge C=A \wedge(B \wedge C), \
&(A \vee B) \vee C=A \vee(B \vee C) .
\end{aligned}
$$
The conjunction operator distributes over the disjunction operator and vice versa.
$$
\begin{aligned}
&A \wedge(B \vee C)=(A \wedge B) \vee(A \wedge C) \
&A \vee(B \wedge C)=(A \vee B) \wedge(A \vee C)
\end{aligned}
$$
The result of the logical conjunction of two propositions is false if one of the propositions is false (irrespective of the value of the other proposition).
$$
A \wedge \mathrm{F}=\mathrm{F} \wedge A=\mathrm{F}
$$
The result of the logical disjunction of two propositions is true if one of the propositions is true (irrespective of the value of the other proposition).
$$
A \vee \mathrm{T}=\mathrm{T} \vee A=\mathrm{T}
$$
The result of the logical disjunction of two propositions, where one of the propositions is known to be false is given by the truth-value of the other proposition. That is, the Boolean value ‘F’ acts as the identity for the disjunction operation.
$$
A \vee \mathrm{F}=A=\mathrm{F} \vee A
$$
The result of the logical conjunction of two propositions, where one of the propositions is known to be true, is given by the truth-value of the other proposition. That is, the Boolean value ‘ $\mathrm{T}$ ‘ acts as the identity for the conjunction operation.
$$
A \wedge \mathrm{T}=A=\mathrm{T} \wedge A
$$
The $\wedge$ and $\vee$ operators are idempotent. That is, when the arguments of the conjunction or disjunction operator are the same, for proposition A, the result is $A$. The idempotent property allows expressions to be simplified.
$$
\begin{aligned}
&A \wedge A=A \
&A \vee A=A
\end{aligned}
$$
The law of the excluded middle is a fundamental property of the propositional calculus. It states that proposition A is either true or false, i.e. there is no third logical value.

命题演算有许多众所周知的性质，例如交换性质、结合性质和分配性质。这些简化了复杂表达式的评估并允许简化逻辑表达式。

交换性质适用于合取和析取算子，它表明两个命题的求值顺序可以颠倒而不影响得到的真值，即
$$
\begin{aligned }
&A \wedge B=B \wedge A \
&A \vee B=B \vee A
\end{aligned}
$$
关联属性成立对于合取和析取算子。这意味着子表达式的求值顺序不会影响得到的真值，即
246
15 命题和谓词逻辑
$$
\begin{aligned}
&(A \wedge B) \wedge C=A \wedge(B \wedge C), \
&(A \vee B) \vee C=A \vee(B \vee C) .
\end{aligned}
$$
合取运算符分布在析取运算符之上，反之亦然。
$$
\begin{aligned}
&A \wedge(B \ vee C)=(A \wedge B) \vee(A \wedge C) \
&A \vee(B \wedge C)=(A \vee B) \wedge(A \vee C)
\end{aligned}
$$
如果其中一个命题为假（与另一个命题的值无关），则两个命题的逻辑合取结果为假。
$$
A \wedge \mathrm{F}=\mathrm{F} \wedge A=\mathrm{F}
$$
如果其中一个命题为真，则两个命题的逻辑析取结果为真（与其他命题的价值无关）。
$$
A \vee \mathrm{T}=\mathrm{T} \vee A=\mathrm{T}
$$
吨两个命题逻辑分离的结果，其中一个命题已知为假，由另一个命题的真值给出。也就是说，布尔值“F”作为析取操作的标识。
$$
A \vee \mathrm{F}=A=\mathrm{F} \vee A
$$
两个命题的逻辑合取结果，其中一个命题已知为真，由另一个命题的真值给出。也就是说，布尔值’$\mathrm{T}$’充当合取运算的标识。
$$
A \wedge \mathrm{T}=A=\mathrm{T} \wedge A
$$
$\wedge$ 和 $\vee$ 运算符是幂等的。也就是说，当合取或析取操作符的参数相同时，对于命题A，结果为$A$。幂等属性允许简化表达式。
$$
\begin{aligned}
&A \wedge A=A \
&A \vee A=A
\end {aligned}
$$
排中律是命题演算的基本性质。它表明命题 A 是真或假，即没有第三个逻辑值。

$A$ 和 $B$ 的合取（表示为 $A \wedge B$ ）当且仅当 $A$ 和 $B$ 都为真时为真，并且在所有其他情况下为假（表 15.2） .两个命题 $\mathrm{A}$ 和 $\mathrm{B}$ 的析取（表示为 $A \vee B$ ）如果 $A$ 和 $B$ 至少有一个为真，则为真，并且全部为假其他情况（表 15.3）。析取运算符被称为“包含或”运算符，因为它在 $A$ 和 $B$ 都为真时也为真；还有一个异或运算符，当 $A$ 或 $B$ 之一为真时为真，否则为假。
示例 15.1 考虑由“橙子是水果”给出的命题 A 和由下式给出的命题 B ‘ $2+2=5$ ‘，则 $A$ 为真，$B$ 为假。因此
(i) $A \wedge B$ （即橙子是水果并且 $2+2=5$ ）是假的，
(ii) $A \vee B$ （即橙子是水果或 $2+2=5$ ) 为真。

命题演算有许多众所周知的性质，例如交换性质、结合性质和分配性质。这些简化了复杂表达式的评估并允许简化逻辑表达式。

真值表给出了最重要的逻辑连接词的操作定义，它们提供了一种机制来确定更复杂的复合表达式的真值。复合表达式由命题和连接词组成，包含多个命题变量的复合表达式的真值由潜在的命题变量和逻辑连接词确定。

命题演算有许多众所周知的性质，例如交换性质、结合性质和分配性质。这些简化了复杂表达式的评估并允许简化逻辑表达式。

图论代考

本章简要介绍了逻辑，它涉及推理和确定论证的有效性。它允许根据逻辑规则从前提推导出结论，并且只要前提为真，逻辑论证就可以确定结论的真实性。

逻辑起源于对真理的本质感兴趣的希腊人。苏格拉底以破坏对手的立场而闻名（这意味着他在辩论中没有赢得任何朋友），而苏格拉底的调查由问答组成，其中对手将被引导得出与他原来的立场不符的结论。他的做法表明他的对手的立场是不连贯的和站不住脚的。

亚里士多德在逻辑方面做了重要的工作，他开发了一套逻辑系统，即三段论逻辑，一直使用到 19 世纪。三段论逻辑是一种“术语逻辑”，字母用来代表单个术语。三段论由两个前提和一个结论组成，其中结论是对两个前提的有效演绎。斯多葛派发展了一种早期形式的命题逻辑，其中可断言（命题）具有真值，它们要么是真要么是假。
George Boole 在 1800 年代中期发展了他的符号逻辑，它后来形成了数字计算的基础。布尔认为，逻辑应该被视为数学的一个独立分支，而不是哲学的一部分。他认为存在数学定律来表达人类思维中的推理操作，并且他展示了亚里士多德的三段论逻辑如何可以简化为一组代数方程。

Gottlob Frege 对逻辑和数学基础做出了重要贡献。他试图证明数学（或至少算术）的所有基本真理都可以从一组有限的逻辑公理中推导出来（这种方法被称为逻辑主义）。他发明了谓词逻辑以及全称和存在量词，谓词逻辑是亚里士多德三段论逻辑的重大进步。
参考文献
239

Ackrill JL (1994) 哲学家亚里士多德。克拉伦登出版社牛津
Boole G (1848) 逻辑演算。 Camb Dublin Math J. III:183-98
Boole G (1854) 对思想规律的调查。多佛出版物。 1854 年首次出版
麦克海尔 D (1985) 布尔。科克大学出版社
O’ Regan G (2013) 计算巨人。施普林格
Shannon C (1937) 继电器和开关电路的符号分析。硕士论文。麻省理工学院

数学代写| DISCRETE MATHEMATICS代考请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

Cryptosystem
A system that describes how to encrypt or decrypt messages
Plaintext
Message in its original form
Ciphertext
Message in its encrypted form
Cryptographer
Invents encryption algorithms
Cryptanalyst
Breaks encryption algorithms or implementations

编码理论代写

编码理论（英语：Coding theory）是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错，最近也用于网络编码中。不同学科（如信息论、电机工程学、数学、语言学以及计算机科学）都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正（或检测）数据传输中的错误。

编码共分四类：^[1]