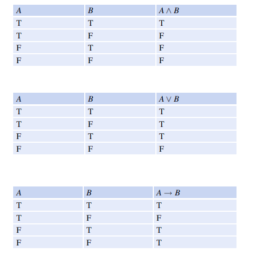
博弈论代写代考| Mixed-Strategy Constant-Sum Games 数学代写
博弈论代考
In this section, we will begin our study of two-person constant-sum games that are not strictly
determined. However, we begin by solving just one more strictly determined game: it is the Antares
vs. Bellatrix game that was the infinite game in Example $6.5$ of Section $6.1$. It will turn out that,
despite being strictly determined and despite being infinite, the ideas behind its solution will be
useful for solving $2 \times 2$ games that are not strictly determined. Once we understand how to solve
$2 \times 2$ games, we will build up to larger games by various techniques until we are finally able to
solve any two-person constant-sum game of any size using linear programming.
6.3.1 Antares vs. Bellatrix
Recall the folloping example from Section 6.1: Antares Industries and Bellatrix, Inc., are the only
two companies that sell a certain computer chip, the Pentangle 5.1. There is an estimated market
for 400,000 of these chips in the year 2021 . Each company must set its prices. Production costs
dictate that the price must be at least $\$ 80$ per chip, while industry regulations dictate that the
set by Bellatrix. Based on reliable market studies of which both companies are aware, it has been
determined that the percentage of the total market which goes to Antares depends on $x$ and $y$ and
is reasonably approximated by the function given by
$E(x, y)=330-3 x-2.7 y+0.03 x y$.
nd $y$ that each company should choose, if their goal is to obtain the
re?
of this game, we observed that this can be regarded as a two-person
rategies for each company are the prices they set ( $x$ and $y$ ). The values
in the real interval [80, 120], so each player has an infinite number
are chosen, then Antares receives a payoff of $E(x, y)$ while Bellatrix
$E(x, y)$. These numbers are percentages of the total market, so they sum
vected.
company chooses a price $x$ ); the column player (Bellatrix) choose a
wooses a price $y$ ); and entering $E(x, y)$ at the point in the matrix where
$y$ meet (We encourage the reader to review his or her solutions to
tion $6.1$, which were finite versions of this game.) Then, we search for
(see Exercises 13 and 14 in Section $6.2$ ).
What are the prices $x$ and $y$ that each company should choose, if their goal is to obtain the
largest-possible market share?
In our earlier discussion of this game, we observed that this can be regarded as a two-person
constant-sum game. The strategies for each company are the prices they set $(x$ and $y)$. The values
of these variables must be in the real interval $[80,120]$, so each player has an infinite number
of strategies. Once $x$ and $y$ are chosen, then Antares receives a payoff of $E(x, y)$ while Bellatrix
receives a payoff of $100-E(x, y)$
If the game were finite, we would construct the payoff matrix by letting the row player (Antares) the constant 100 , as expected.
choose a row (that is, the company chooses a price $x$ ); the column player (Bellatrix) choose a
column (that is, Bellatrix chooses a price $y$ ); and entering $E(x, y)$ at the point in the matrix where
the row $x$ and the column $y$ meet (We encourage the reader to review his or her solutions to
Exercises 6,7 , and 8 in Section $6.1$, which were finite versions of this game.) Then, we search for
a saddle point in this matrix (see Exercises 13 and 14 in Section 6.2).
In our case, since we have infinitely many choices for $x$ and $y$, it does not make sense to
construct a matrix, but it should be clear that the function $E(x, y)$ serves the exact same purpose
as the payoff matrix – it gives, for each choice $(x, y)$, the payoff $E(x, y)$ to the row player Antares.
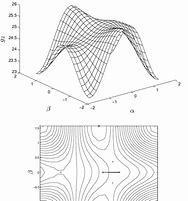
The attentive reader will recognize that the graph of $E(x, y)$ is a surface. So for such infinite,
continuous games, this surface replaces the payoff matrix. Of course, we are only concerned with
that part of the surface which is defined for $x \in[80,120]$ and similarly for $y$.
Now, the argument that a saddle point in the payoff matrix is the same thing as a Nash equilib-
rium, which we gave in Proposition $6.11$ of Section $6.2$, is actually still valid when applied to this
surface. A choice of $(x, y)$ for which $E(x, y)$ is simultaneously a minimum in its “row” (being in a
row means holding $y$ fixed) and a maximum in its “column” (which means holding $x$ fixed) will
represent an outcome of the game where neither player stands to gain by a unilateral change in
$E(x, y)$ in the relevant ranges for $x$ and $y$.
$E(x, y)$ in the relevant ranges for $x$ and $y$. Finally, the reader should recall Chapter 1 , where we studied surfaces of the form $F(x, y)=$
$A-B x-C y+D x y$. We saw that any function of this form was called a saddle surface precisely
because it could always be converted to standard form $F(x, y)=D(x-p)(y-q)+v$, which is
a surface with a saddle point at the location $(x, y)=(p, q)$ and where $F(p, q)=v$. Thus, to solve
the Antares vs. Bellatrix infinite game, we must put $E(x, y)$ into standard form. By the techniques
we discussed in Chapter 1 , the standard form of $E(x, y)$ is
$E(x, y)=.03(x-90)(y-100)+60 .$
we discussed in Chapter 1 , the standard form of $E(x, y)$ is
$$
E(x, y)=03(x-00)(y-100)+60
$$
Therefore, there is a saddle point at $(x, y)=(90,100)$ and $E(00,100)=60 .$ Notice that the
Therefore, there is a saddle point at $(x, y)=(90,100)$ and $E(90,100)=60$. Notice that the saddle point is located in the required range of prices $80 \leq x, y \leq 120$. Therefore, the Antares
saddle point is located in the required range of prices $80 \leq x, y \leq 120 .$ Therefore, the Antares
vs. Bellatrix game is strictly determined (even though it is infinite). Antares should set its price at
$\$ 90 ;$ Bellatrix should set its price at $\$ 100$. If they both follow this recommendation, the value of
the game is $v=60$. Thus, Antares will have $60 \%$ of the market, and Bellatrix will have $40 \%$.
Since this is a Nash equilibrium, if either player were to unilaterally deviate from this strategy,
we might expect the payoff in market shares to the other player to possibly improve. But actually,
in this game, that does not happen. For example, if Antares sets its price at the optimum choice
of $\$ 90$ per chip, then by evaluating (6.2), it is clear that $E(90, y)=60$ for all $y$. So in this case,
if Bellatrix changes its price unilaterally, it won’t affect the payoff to Antares at all. Similarly, if
Bellatrix sets its price at the optimum of $\$ 100$ per chip, a unilateral change in price by Antares
will not affect its payoff since $E(x, 100)=60$ for any $x$. (Not all saddle points behave this way,
but if the game is one where the payoffs are given by a saddle surface function of crossed type,
We remark in passing that we can also find the revenue for each company Assuming a total
market of 400,000 chips, the total revenue for Antares is $\$ 400,000\left(\frac{E}{\operatorname{tcog}}\right) x=\$ 400,000(0.6)(90)=$
$\$ 21,600,000 ;$ and the revenue for Bellatrix is $\$ 400,000\left(\frac{100-E}{100}\right) y=\$ 400,000(0.4)(100)=$
$\$ 16,000,000$. Remember, however, that the goal of each company is to maximize market shares,
not revenue, since we observed previously a game with revenues as payoffs would be variable-sum.
在本节中,我们将开始研究不严格的两人常数和博弈
决定。然而,我们首先解决一个更严格的游戏:它是 Antares
vs. Bellatrix 游戏,即 $6.1$ 的示例 $6.5$ 中的无限游戏。事实证明,
尽管被严格确定并且尽管是无限的,但其解决方案背后的想法将是
对于解决没有严格确定的 $2 \times 2$ 游戏很有用。一旦我们了解如何解决
$2 \times 2$ 游戏,我们将通过各种技术构建更大的游戏,直到我们最终能够
使用线性规划解决任何规模的任何两人常数和游戏。
6.3.1 Antares 与 Bellatrix
回想第 6.1 节中的以下示例: Antares Industries 和 Bellatrix, Inc. 是唯一的
两家销售某种计算机芯片 Pentangle 5.1 的公司。估计有市场
在 2021 年购买 400,000 个这样的芯片。每个公司都必须设定价格。生产成本
规定价格必须至少为每芯片 $\$ 80$,而行业法规规定
由贝拉特里克斯设定。根据两家公司都知道的可靠市场研究,它已经
确定进入 Antares 的总市场的百分比取决于 $x$ 和 $y$ 和
由下式给出的函数合理地近似
$E(x, y)=330-3 x-2.7 y+0.03 x y$。
nd $y$ 每个公司应该选择,如果他们的目标是获得
回覆?
在这个游戏中,我们观察到这可以看作是一个两人
每家公司的费率是他们设定的价格( $x$ 和 $y$ )。价值
在实数区间 [80, 120] 中,所以每个玩家都有无限个数
被选中,则 Antares 获得 $E(x, y)$ 而 Bellatrix
$E(x, y)$。这些数字是整个市场的百分比,所以它们总和
受害。
公司选择价格 $x$ );专栏玩家(贝拉特里克斯)选择一个
追求价格 $y$ );并在矩阵中的点输入 $E(x, y)$
$y$ meet(我们鼓励读者回顾他或她的解决方案
$6.1$,这是这个游戏的有限版本。)然后,我们搜索
(参见第 6.2$ 节中的练习 13 和 14)。
如果每家公司的目标是获得
最大的市场份额?
在我们之前对这个游戏的讨论中,我们观察到这可以看作是一个两人
恒和博弈。每家公司的策略是他们设定的价格 $(x$ 和 $y)$。价值
这些变量中的一个必须在实际区间 $[80,120]$ 内,因此每个玩家都有无限个数
的策略。一旦选择了 $x$ 和 $y$,Antares 将获得 $E(x, y)$ 的回报,而 Bellatrix
获得 $100-E(x, y)$ 的回报
如果游戏是有限的,我们将通过让行者(Antares)为常数 100 来构造收益矩阵,正如预期的那样。
选择一行(即公司选择价格 $x$ );专栏玩家(贝拉特里克斯)选择一个
列(即 Bellatrix 选择价格 $y$ );并在矩阵中的点输入 $E(x, y)$
$x$ 行和 $y$ 列相遇(我们鼓励读者回顾他或她的解决方案
$6.1$ 中的练习 6,7 和 8,它们是这个游戏的有限版本。)然后,我们搜索
该矩阵中的一个鞍点(参见第 6.2 节中的练习 13 和 14)。
在我们的例子中,因为我们对 $x$ 和 $y$ 有无限多的选择,所以没有意义
构造一个矩阵,但应该清楚的是,函数 $E(x, y)$ 的用途完全相同
作为收益矩阵 – 对于每个选择 $(x, y)$,它给出了行玩家 Antares 的收益 $E(x, y)$。
细心的读者会认识到$E(x, y)$ 的图是一个曲面。所以对于这样的无限,
连续博弈,这个表面代替了收益矩阵。当然,我们只关心
为 $x \in[80,120]$ 和 $y$ 定义的表面部分。
现在,收益矩阵中的鞍点与纳什均衡相同的论点
我们在 $6.2$ 的提案 $6.11$ 中给出的 rium 在应用于此时实际上仍然有效
表面。一个 $(x, y)$ 的选择,其中 $E(x, y)$ 在它的“行”中同时是最小值(在一个
行意味着保持 $y$ 固定)并且其“列”中的最大值(这意味着保持 $x$ 固定)将
代表博弈的结果,其中任何一方都无法通过单方面的改变获得收益
$E(x, y)$ 在 $x$ 和 $y$ 的相关范围内。
$E(x, y)$ 在 $x$ 和 $y$ 的相关范围内。最后,读者应该回忆一下第 1 章,在那里我们研究了 $F(x, y)=$ 形式的曲面
$A-B x-C y+D x y$。我们看到,这种形式的任何函数都被精确地称为鞍面
因为它总是可以转换为标准形式 $F(x, y)=D(x-p)(y-q)+v$,即
在 $(x, y)=(p, q)$ 和 $F(p, q)=v$ 处有一个鞍点的曲面。因此,要解决
Antares vs. Bellatrix 无限游戏,我们必须将 $E(x, y)$ 转换为标准形式。通过技术
我们讨论
博弈论代写
博弈论是关于什么的?当我妻子外出参加托斯卡纳的一个愉快的小型会议时,三位年轻女性邀请我与她们同桌共进午餐。当我坐下时,其中一个用闷热的声音说,“教我们如何玩爱情游戏”,但事实证明,他们想要的只是关于如何管理意大利男朋友的建议。我仍然认为他们拒绝我的战略建议是错误的,但他们正确地认为求爱是我们在现实生活中玩的许多不同类型的游戏之一在交通繁忙的司机正在玩驾驶游戏。在 eBay 上竞标的讨价还价者正在玩拍卖游戏。一家公司和一个工会正在谈判明年的工资,这是一场讨价还价的游戏。当反对的候选人在选举中选择他们的平台时,他们正在玩一场政治游戏。决定今天玉米片价格的杂货店老板正在玩一场经济游戏。简而言之,每当人类互动时,就会玩游戏。
每次新的巨额电信拍卖都需要根据将要运行的环境进行调整。不能像美国政府在聘请苏富比拍卖一堆卫星转发器时发现的那样,将设计从货架上拿下来。但也无法在数学模型中捕捉到新电信市场的所有复杂细节。因此,设计电信拍卖既是一门艺术,也是一门科学。一个人从简单的模型中推断出来,这些模型被选择来模仿似乎是问题的基本战略特征。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
博弈论,又称为对策论(Game Theory)、赛局理论等,既是现代数学的一个新分支,也是运筹学的一个重要学科。 博弈论主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。 博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。