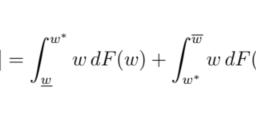数学代写|Density of certain sets of holomorphic functions 数论代考
数论代考
Let $D$ be a non-empty open disc in $C$ and $\bar{D}$ its closure. We denote by $H(D)$ the Banach space of all continuous functions $f: \overline{\mathrm{D}} \longrightarrow \mathrm{C}$ which are holomorphic in D, with the norm
$$
|f|_{\infty}=\sup {z \in \overline{\mathrm{D}}}|f(z)| . $$ We also denote by $\mathrm{C}(\mathrm{K})$ the Banach space of continuous functions on a compact space $\mathrm{K}$, also with the norm $$ |f|{\infty}=\sup {x \in \mathrm{K}}|f(x)| $$ (so that there is no risk of confusion if $\mathrm{K}=\mathrm{D}$ and we apply this to a function that also belongs to $\mathrm{H}(\mathrm{D})$ ). We denote by $\mathrm{C}(\mathrm{K})^{\prime}$ the dual of $\mathrm{C}(\mathrm{K})$, namely the space of continuous linear functionals $\mathrm{C}(\mathrm{K}) \longrightarrow \mathrm{C}$. An element $\mu \in \mathrm{C}(\mathrm{K})^{\prime}$ can also be interpreted as a complex measure on $\mathrm{K}$ (by the Riesz-Markov Theorem, see e.g. [40, Th. 7.17]), and in this interpretation one would write $$ \mu(f)=\int{\mathrm{K}} f(x) d \mu(x)
$$
for $f \in \mathrm{C}(\mathrm{K})$.
THEOREM A.5.1. Let $\mathrm{D}$ be as above. Let $\mid\left(f_{n}\right){n \geqslant 1}$ be a sequence of elements of $\mathrm{H}(\mathrm{D})$ with $\sum{n \geqslant 1}\left|f_{n}\right|_{\infty}^{2}<+\infty$ $\left(\alpha_{n}\right)$ of complex numbers with $\left|\alpha_{n}\right|=1$ such that the Let $\mathrm{X}$ be the set series nverges in $\mathrm{H}(\mathrm{D})$.
converges in $\mathrm{H}(\mathrm{D})$. Assume that $\mathrm{X}$ is not empty and that, for any continuous linear functional $\mu \in \mathrm{C}(\overline{\mathrm{D}})^{\prime}$ such that
$$
\sum_{n \geqslant 1}\left|\mu\left(f_{n}\right)\right|<+\infty
$$
the Laplace transform of $\mu$ is identically 0 . Then for any $\mathrm{N} \geqslant 1$, the set of series
$$
\sum_{n \geqslant \mathrm{~N}} \alpha_{n} f_{n}
$$
for $\left(\alpha_{n}\right)$ in $\mathrm{X}$ is dense in $\mathrm{H}(\mathrm{D})$.
Here, the Laplace transform of $\mu$ is defined by
LemmA A.5.2. Let $\mathrm{K}$ be a complex subset of $\mathrm{C}$ and $\mu \in \mathrm{C}(\mathrm{K})^{\prime}$ a continuous linear complex measure on $C$ that is supported on $\bar{D}$, one would write for $\left(f_{n}\right){n>\mathrm{N}}$, hence the general case follows. Laplace transform is zero in certain circumstances. functional. Let $$ g(z)=\int e^{w z} d \mu(z)=\mu\left(w \mapsto e^{w z}\right) $$ be its Laplace transform. (1) The function $g$ is an entire function on $\mathbf{C}$, i.e., it is holomorphic on $\mathrm{C}$. (2) We have $$ \limsup {|z| \rightarrow+\infty} \frac{\log |g(z)|}{|z|}<+\infty
$$
(3) If $g \neq 0$, then
$$
\limsup {r \rightarrow+\infty} \frac{\log |g(r)|}{r} \geqslant \inf {z \in \mathrm{K}} \operatorname{Re}(z)
$$
PROOF. (1) Let $z \in \mathbf{C}$ be fixed. For $h \neq 0$, we have
$$
g(z+h)-g(z)=u\left(f_{h}\right)
$$
令$D$ 是$C$ 中的一个非空开圆盘,$\bar{D}$ 是它的闭包。我们用 $H(D)$ 表示所有连续函数 $f 的 Banach 空间: \overline{\mathrm{D}} \longrightarrow \mathrm{C}$ 在 D 中是全纯的,具有范数
$$
|f|_{\infty}=\sup {z \in \overline{\mathrm{D}}}|f(z)| . $$ 我们还用 $\mathrm{C}(\mathrm{K})$ 表示紧致空间 $\mathrm{K}$ 上的连续函数的 Banach 空间,同样具有范数 $$ |f|{\infty}=\sup {x \in \mathrm{K}}|f(x)| $$ (因此如果 $\mathrm{K}=\mathrm{D}$ 并且我们将其应用于也属于 $\mathrm{H}(\mathrm{D})$ 的函数,则不会有混淆的风险)。我们用 $\mathrm{C}(\mathrm{K})^{\prime}$ 表示 $\mathrm{C}(\mathrm{K})$ 的对偶,即连续线性泛函空间 $\mathrm {C}(\mathrm{K}) \longrightarrow \mathrm{C}$。元素 $\mu \in \mathrm{C}(\mathrm{K})^{\prime}$ 也可以解释为 $\mathrm{K}$ 上的复测度(根据 Riesz-Markov 定理,参见例如 [40, Th. 7.17]),在这种解释中,人们会写 $$ \mu(f)=\int{\mathrm{K}} f(x) d \mu(x)
$$
对于 $f \in \mathrm{C}(\mathrm{K})$。
定理 A.5.1。令 $\mathrm{D}$ 如上。设 $\mid\left(f_{n}\right){n \geqslant 1}$ 是 $\mathrm{H}(\mathrm{D})$ 的元素序列 $\sum{n \geqslant 1}\left|f_{n}\right|_{\infty}^{2}<+\infty$ $\left(\alpha_{n}\right)$ 复数具有 $\left|\alpha_{n}\right|=1$ 的数使得设 $\mathrm{X}$ 为集合级数收敛于 $\mathrm{H}(\mathrm{D})$。
收敛于 $\mathrm{H}(\mathrm{D})$。假设 $\mathrm{X}$ 不为空,并且对于任何连续线性泛函 $\mu \in \mathrm{C}(\overline{\mathrm{D}})^{\prime}$ 使得
$$
\sum_{n \geqslant 1}\left|\mu\left(f_{n}\right)\right|<+\infty
$$
$\mu$ 的拉普拉斯变换完全相同 0 。那么对于任何 $\mathrm{N} \geqslant 1$,系列的集合
$$
\sum_{n \geqslant \mathrm{~N}} \alpha_{n} f_{n}
$$
对于$\mathrm{X}$ 中的$\left(\alpha_{n}\right)$,在$\mathrm{H}(\mathrm{D})$ 中是稠密的。
这里,$\mu$ 的拉普拉斯变换定义为
引理 A.5.2。令 $\mathrm{K}$ 是 $\mathrm{C}$ 和 $\mu \in \mathrm{C}(\mathrm{K})^{\prime}$ 的复子集$\bar{D}$ 支持的 $C$,可以写成 $\left(f_{n}\right){n>\mathrm{N}}$,因此一般情况如下。在某些情况下,拉普拉斯变换为零。功能性的。让 $$ g(z)=\int e^{w z} d \mu(z)=\mu\left(w \mapsto e^{w z}\right) $$ 是它的拉普拉斯变换。 (1) 函数 $g$ 是 $\mathbf{C}$ 上的一个整函数,即它是 $\mathrm{C}$ 上的全纯函数。 (2) 我们有 $$ \limsup {|z| \rightarrow+\infty} \frac{\log |g(z)|}{|z|}<+\infty
$$
(3) 如果$g \neq 0$,那么
$$
\limsup {r \rightarrow+\infty} \frac{\log |g(r)|}{r} \geqslant \inf {z \in \mathrm{K}} \operatorname{Re}(z)
$$
证明。 (1) 令 $z \in \mathbf{C}$ 固定。对于 $h \neq 0$,我们有
$$
\下划线{g(z+h)-g(z)}=u\left(f_{h}\right)
$$
数论代写
数论是纯粹数学的分支之一,主要研究整数的性质。整数可以是方程式的解(丢番图方程)。有些解析函数(像黎曼ζ函数)中包括了一些整数、质数的性质,透过这些函数也可以了解一些数论的问题。透过数论也可以建立实数和有理数之间的关系,并且用有理数来逼近实数(丢番图逼近)。
按研究方法来看,数论大致可分为初等数论和高等数论。初等数论是用初等方法研究的数论,它的研究方法本质上说,就是利用整数环的整除性质,主要包括整除理论、同余理论、连分数理论。高等数论则包括了更为深刻的数学研究工具。它大致包括代数数论、解析数论、计算数论等等。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
在中世纪时,除了1175年至1200年住在北非和君士坦丁堡的斐波那契有关等差数列的研究外,西欧在数论上没有什么进展。
数论中期主要指15-16世纪到19世纪,是由费马、梅森、欧拉、高斯、勒让德、黎曼、希尔伯特等人发展的。最早的发展是在文艺复兴的末期,对于古希腊著作的重新研究。主要的成因是因为丢番图的《算术》(Arithmetica)一书的校正及翻译为拉丁文,早在1575年Xylander曾试图翻译,但不成功,后来才由Bachet在1621年翻译完成。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。