经济代写 | Axioms: convexity, monotonicity, and continuity 微观经济学代写
经济代写
3.1. Convex preferences. We will often assume convexity of preferences and monotonicity. We will first need some math.
70
IV. ORDINAL PREFERENCE THEORY
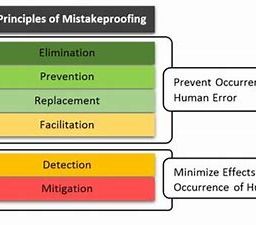
FIGURE IV.7. Convex sets?
DefinItiON IV 17 (CONVEX COMBINATION). Let $x$ and $y$ be elements of $\mathbb{R}^{\ell}$. Then,
$$
k x+(1-k) y, k \in[0,1]
$$
is called the convex combination of $x$ and $y$.
We have seen a convex combination before, in exercise IV.1 (p. 59). The convex combination of $x$ and $y$ lies on the line connecting $x$ and $y$. The smaller $k$, the closer the convex combination to $y$, which is also clear from
$$
k x+(1-k) y=y+k(x-y) \text {. }
$$
DEFINITION IV.18 (CONVEX SET). A set $M \subseteq \mathbb{R}^{\ell}$ is called convex if for any two points $x$ and $y$ from $M$, their convex combinations are also contained in $M$.
Here, convexity is a property of sets and is not to be confused with the convexity of functions. In figure IV.7, the left-hand example shows a set that is not convex, while the other two sets exhibit convexity.
EXERCISE IV.12. Show that the intersection of two convex sets is also convex.
DEFINITION IV.19 (STRICTLY CONVEX SET). A set $M$ is called strictly convex if for any two points $x$ and $y$ from $M, x \neq y$,
$$
k x+(1-k) y
$$
is an interior point of $M$ for any $k \in(0,1)$.
The right-most set in figure IV.7 is strictly convex, while the middle set is convex but not strictly so. Convince yourself that open $\varepsilon-b a l l s ~ i n ~ \mathbb{R}^{2}$ are strictly convex for any norm. How about closed $\varepsilon-b a l l s ?$
EXERCISE IV. 13. Are the intervals $(0, \infty),[0,3]$, or $[0, \infty)$ convex or strictly convex?
- AXIOMS: CONVEXITY, MONOTONICITY, AND CONTINUITY
71
FIGURE IV.8. Two interior points
DEFINITION IV.20 (CONVEX PREFERENCE RELATION). A preference relation $\succ$ on $\mathbb{R}_{+}^{\ell}$ is
- convex if all its better sets $B_{y}$ are convex,
- strictly convex if all its better sets $B_{y}$ are strictly convex,
- concave if all its worse sets $W_{y}$ are convex,
- strictly concave if all its worse sets $W_{y}$ are strictly convex.
A rough description of convexity is “mixtures are prefered to extremes”.
I, for example, would rather have 1 glass of milk and one donut than two
3.1。凸偏好。我们通常会假设偏好的凸性和单调性。我们首先需要一些数学知识。
70
四。序数偏好理论
图 IV.7。凸集?
定义 IV 17(凸组合)。令 $x$ 和 $y$ 是 $\mathbb{R}^{\ell}$ 的元素。然后,
$$
k x+(1-k) y, k \in[0,1]
$$
称为$x$ 和$y$ 的凸组合。
我们之前在练习 IV.1(第 59 页)中已经看到了一个凸组合。 $x$ 和 $y$ 的凸组合位于连接 $x$ 和 $y$ 的直线上。 $k$越小,凸组合越接近$y$,这也可以从
$$
k x+(1-k) y=y+k(x-y) \text {. }
$$
定义 IV.18(凸集)。一个集合 $M \subseteq \mathbb{R}^{\ell}$ 称为凸集,如果对于来自 $M$ 的任意两点 $x$ 和 $y$,它们的凸组合也包含在 $M$ 中。
这里,凸性是集合的属性,不要与函数的凸性混淆。在图 IV.7 中,左边的例子显示了一个非凸的集合,而其他两个集合表现出凸性。
练习 IV.12。证明两个凸集的交集也是凸的。
定义 IV.19(严格凸集)。一个集合 $M$ 称为严格凸集,如果对于来自 $M 的任意两点 $x$ 和 $y$,x \neq y$,
$$
k x+(1-k) y
$$
是任何 $k \in(0,1)$ 的 $M$ 的内点。
图 IV.7 中最右边的集合是严格凸的,而中间的集合是凸的但并非严格如此。说服自己 open $\varepsilon-b a l l s ~ i n ~ \mathbb{R}^{2}$ 对于任何范数都是严格凸的。关闭 $\varepsilon-b a l l s 怎么样?$
练习四。 13.区间$(0,\infty),[0,3]$,或$[0,\infty)$是凸的还是严格凸的?
- 公理:凸性、单调性和连续性
71
图 IV.8。两个内点
定义 IV.20(凸偏好关系)。 $\mathbb{R}_{+}^{\ell}$ 上的偏好关系 $\succ$ 是
- 如果所有更好的集合 $B_{y}$ 都是凸的,则为凸的,
- 如果所有更好的集合 $B_{y}$ 都是严格凸的,则严格凸的,
- 如果所有较差的集合 $W_{y}$ 都是凸的,则为凹的,
- 如果所有较差的集合 $W_{y}$ 都是严格凸的,则严格凹。
对凸性的粗略描述是“混合物优于极端”。
例如,我宁愿喝 1 杯牛奶和一个甜甜圈,也不愿两个
经济代考
微观经济学又称个体经济学,小经济学,是宏观经济学的对称。 微观经济学主要以单个经济单位( 单个的生产者、单个的消费者、单个市场的经济活动)作为研究对象,分析单个生产者如何将有限的资源分配在各种商品的生产上以取得最大的利润;单个消费者如何将有限的收入分配在各种商品的消费上以获得最大的满足。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
微观经济学 是研究人们和企业在资源分配、商品和服务交易价格等方面做出的决策。它考虑税收、法规和政府立法。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。