经济代写 | The vector space of goods. 微观经济学代写
经济代写
1.1. The vector space of goods. Our household is confronted with a finite number $\ell$ of goods. These goods have certain characteristics (for example, apples of a certain weight and class) and are further differentiated according to the region, where they are on offer, and the time interval during which they can be bought. It is also possible to define contingent products, i.e., products distinguished by states of nature. The good in question may be 4 pounds of apple of certain characteristics to be delivered at time $t$ if 0. Thus, it may well happen that payments occur but apples cannot be consumed (rain the day before in our example).
Formally, bundles of goods are elements of the vector space $\mathbb{R}^{\ell}$. The real line depicts the set of real numbers, $\mathbb{R}$. The set of all vectors with two real numbers, $\mathbb{R}^{2}$, is visualized by the two-dimensional plane, while the set of all vectors with three real numbers, $\mathbb{R}^{3}$, represents the three-dimensional space. You know how to calculate in a vector space?
EXERCISE IV.1. Consider the vectors $x=\left(x_{1}, x_{2}\right)=(2,4)$ and $y=\left(y_{1}, y_{2}\right)=$ $(8,12)$. Find $x+y, 2 x$, and $\frac{1}{4} x+\frac{3}{4} y$ !
$\frac{1}{4} x+\frac{3}{4} y$ is called a convex combination of vectors $x$ and $y$ because the coefficients are non-negative and they sum to 1 . It is to be found on the line between $x$ and $y$. $\frac{1}{4} x+\frac{3}{4} y$ is closer to $y$ because $y$ ‘s coefficient is the highest. An extreme case is $0 x+1 y=y$.
59
(C) The Author(s), under exclusive license to
Springer Fachmedien Wiesbaden GmbH, part of Springer Nature 2021
H. Wiese, Advanced Microeconomics,
https://doi.org/10.1007/978-3-658-34959-2_4
60
IV. ORDINAL PREFERENCE THEORY
In general (for an arbitrary dimension $\ell \in \mathbb{N}$ ) we write
$$
\mathbb{R}^{\ell}:=\left{\left(x_{1}, \ldots, x_{\ell}\right): x_{g} \in \mathbb{R}, g=1, \ldots, \ell\right} .
$$
$0 \in \mathbb{R}^{\ell}$ is the null vector $(0,0, \ldots, 0)$. The vectors are often called points (in $\mathbb{R}^{\ell}$ ).
REMARK IV.1. For vectors $x$ and $y$ with $\ell$ entries, we define
- $x \geq y$ by $x_{g} \geq y_{g}$ for all $g$ from ${1,2, \ldots, \ell}$,
- $x>y$ by $x \geq y$ and $x \neq y$,
- $x \gg y$ by $x_{g}>y_{g}$ for all $g$ from ${1,2, \ldots, \ell}$.
In household theory, we will work with the goods space
$$
\mathbb{R}{+}^{\ell}:=\left{x \in \mathbb{R}^{\ell}: x \geq 0\right} $$ rather than $\mathbb{R}^{\ell}$ (where negative amounts of goods would be possible). 1.2. Distance and balls. We will need some topological concepts and need to learn how to define the distance between points or how to establish that a set is open or closed. While most of our definitions refer to $\mathbb{R}^{l}$, we sometimes use $\mathbb{R}{+}^{l}$, the goods space, instead.
DEFINITION IV.1 (DISTANCE). In $\mathbb{R}^{\ell}$ the distance between two points $x$ and
$y$ is given by the city-block norm (or 1-norm)
$$
|x-y|_{1}:=\sum_{g=1}^{\ell}\left|x_{g}-y_{g}\right|
$$
by the euclidian (or 2-) norm
$$
|x-y|_{2}:=\sqrt{\sum_{g=1}^{\ell}\left(x_{g}-y_{g}\right)^{2}}
$$
or by the infinity norm
$$
|x-y|_{\infty}:=\max {g=1, \ldots, l}\left|x{g}-y_{g}\right| .
$$
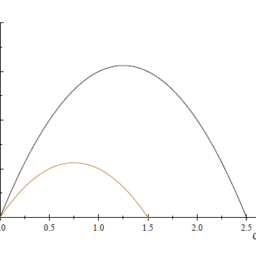
Figure IV.1 illustrates these norms,
When we later define certain terms such as open sets, bounded sets, etc., it is not important which of these norms we use. The three norms above are the most common and have a simple geometric interpretation. What is it? We will often just write $|\cdot|$ and the reader is free to imagine any of these norms.
EXERCISE IV.2. What is the distance (in $\left.\mathbb{R}^{2}\right)$ between $(2,5)$ and $(7,1)$, measured by the 2-norm $|\cdot|_{2}$ and by the inifinity norm ||$_{\infty}$ ?
1.1。商品的向量空间。我们家面临的商品数量有限。这些商品具有一定的特征(例如,一定重量和等级的苹果),并根据地区、销售地点以及可以购买的时间间隔进一步区分。也可以定义或有产品,即按自然状态区分的产品。所讨论的商品可能是 4 磅具有某些特性的苹果,如果为 0,则在时间 $t$ 交付。因此,很可能发生付款发生但苹果不能被消费(在我们的示例中前一天下雨)。
形式上,商品束是向量空间 $\mathbb{R}^{\ell}$ 的元素。实线表示实数集 $\mathbb{R}$。具有两个实数的所有向量的集合 $\mathbb{R}^{2}$ 由二维平面可视化,而具有三个实数的所有向量的集合 $\mathbb{R}^{ 3}$,代表三维空间。你知道如何在向量空间中计算吗?
练习 IV.1。考虑向量 $x=\left(x_{1}, x_{2}\right)=(2,4)$ 和 $y=\left(y_{1}, y_{2}\right)=$ $ (8,12) 美元。求 $x+y、2 x$ 和 $\frac{1}{4} x+\frac{3}{4} y$ !
$\frac{1}{4} x+\frac{3}{4} y$ 被称为向量 $x$ 和 $y$ 的凸组合,因为系数是非负的并且它们总和为 1 。它位于$x$ 和$y$ 之间。 $\frac{1}{4} x+\frac{3}{4} y$ 更接近 $y$ 因为 $y$ 的系数最高。一个极端的情况是$0 x+1 y=y$。
59
(C) 作者,根据独家许可
Springer Fachmedien Wiesbaden GmbH,Springer Nature 2021 的一部分
H. Wiese,高级微观经济学,
https://doi.org/10.1007/978-3-658-34959-2_4
60
四。序数偏好理论
一般来说(对于任意维度 $\ell \in \mathbb{N}$ )我们写
$$
\mathbb{R}^{\ell}:=\left{\left(x_{1}, \ldots, x_{\ell}\right): x_{g} \in \mathbb{R}, g= 1,\ldots,\ell\right}。
$$
$0 \in \mathbb{R}^{\ell}$ 是空向量 $(0,0, \ldots, 0)$。向量通常称为点(在 $\mathbb{R}^{\ell}$ 中)。
备注 IV.1。对于具有 $\ell$ 条目的向量 $x$ 和 $y$,我们定义
- $x \geq y$ by $x_{g} \geq y_{g}$ 对于来自 ${1,2, \ldots, \ell}$ 的所有 $g$,
- $x>y$ 通过 $x \geq y$ 和 $x \neq y$,
- 对于来自 ${1,2, \ldots, \ell}$ 的所有 $g$,$x \gg y$ 通过 $x_{g}>y_{g}$。
在家居理论中,我们将使用商品空间
$$
\mathbb{R}{+}^{\ell}:=\left{x \in \mathbb{R}^{\ell}: x \geq 0\right} $$ 而不是 $\mathbb{R}^{\ell}$(可能出现负数商品)。 1.2.距离和球。我们将需要一些拓扑概念,并且需要学习如何定义点之间的距离或如何确定一个集合是开集还是闭集。虽然我们的大多数定义都引用了 $\mathbb{R}^{l}$,但我们有时使用商品空间 $\mathbb{R}{+}^{l}$ 来代替。
定义 IV.1(距离)。在 $\mathbb{R}^{\ell}$ 中,两点 $x$ 和
$y$ 由街区范数(或 1-范数)给出
$$
|x-y|_{1}:=\sum_{g=1}^{\ell}\left|x_{g}-y_{g}\right|
$$
欧几里得(或 2-)范数
$$
|x-y|_{2}:=\sqrt{\sum_{g=1}^{\ell}\left(x_{g}-y_{g}\right)^{2}}
$$
或通过无穷范数
$$
|x-y|_{\infty}:=\max {g=1, \ldots, l}\left|x{g}-y_{g}\right| .
$$
图 IV.1 说明了这些规范,
当我们稍后定义某些术语(例如开集、有界集等)时,我们使用这些规范中的哪一个并不重要。上述三个规范是最常见的,并且具有简单的几何解释。它是什么?我们通常只写 $|\cdot|$ ,读者可以自由想象这些规范中的任何一个。
练习 IV.2。 $(2,5)$ 和 $(7,1)$ 之间的距离(以 $\left.\mathbb{R}^{2}\right)$ 为单位,由 2 范数 $|\ 测量cdot|_{2}$ 和无穷大范数 ||$_{\infty}$ ?
经济代考
微观经济学又称个体经济学,小经济学,是宏观经济学的对称。 微观经济学主要以单个经济单位( 单个的生产者、单个的消费者、单个市场的经济活动)作为研究对象,分析单个生产者如何将有限的资源分配在各种商品的生产上以取得最大的利润;单个消费者如何将有限的收入分配在各种商品的消费上以获得最大的满足。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
微观经济学 是研究人们和企业在资源分配、商品和服务交易价格等方面做出的决策。它考虑税收、法规和政府立法。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。