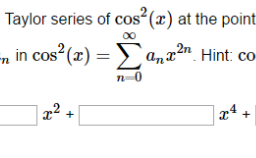微积分(Calculus),数学概念,是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法
my-assignmentexpert™ 微积分calculus作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微积分calculus作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分calculus作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微积分calculus代写服务。我们的专家在微积分calculus学 代写方面经验极为丰富,各种微积分calculus相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 单变量微积分
- 多变量微积分
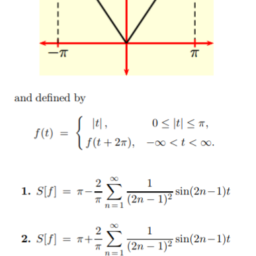
- 傅里叶级数
- 黎曼积分
- ODE
- 微分学
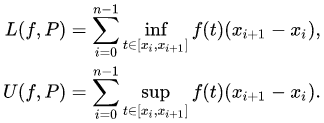
微积分代考calculus代写|Introduction
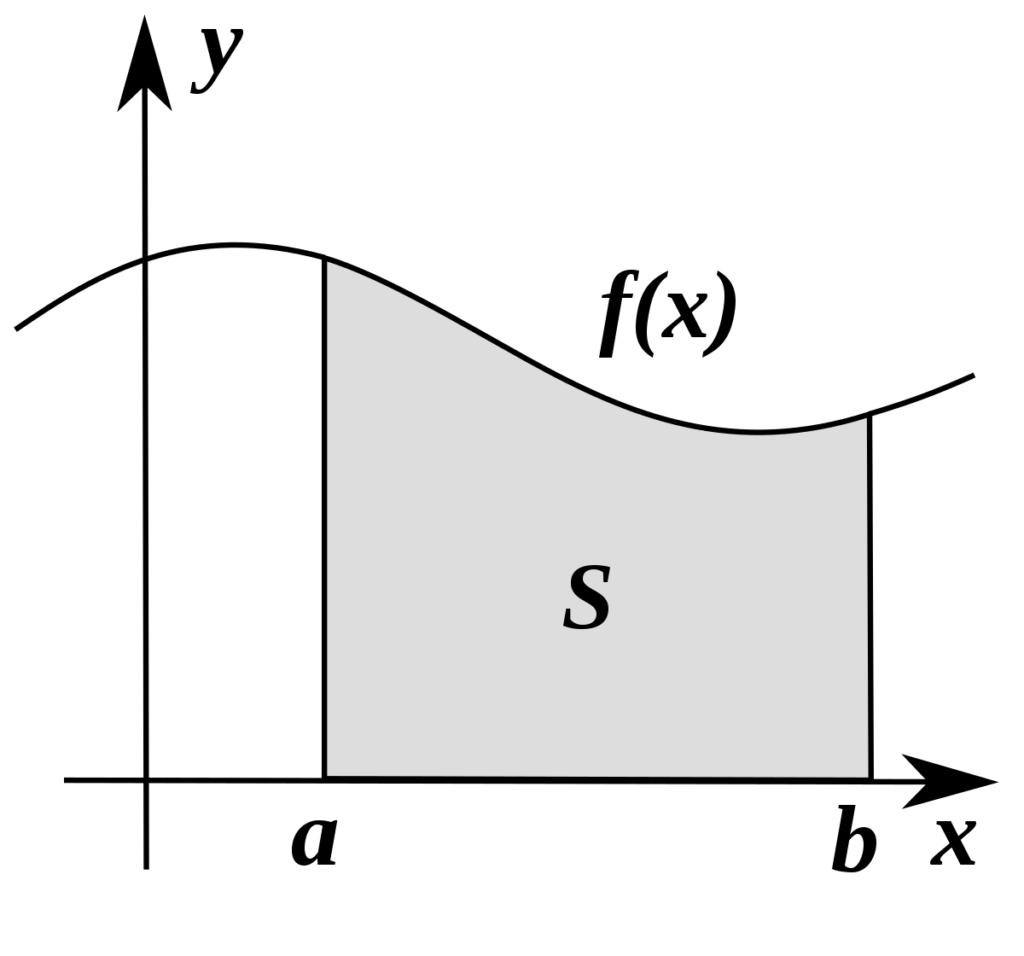
Thus, we get an upper and lower bound for $A$. To get better estimates, let us consider a point $c$ such that $a<c<b$. Then we have
$$
m_{1} \leq f(x) \leq M_{1} \quad \forall x \in[a, c] ; \quad m_{2} \leq f(x) \leq M_{2} \quad \forall x \in[c, b]
$$
where
$$
\begin{array}{ll}
m_{1}=\inf {x \in[a, c]} f(x), \quad m{2}=\inf {x \in[c, b]} f(x), \ M{1}=\sup {x \in[a, c]} f(x), \quad M{2}=\sup {x \in[c, b]} f(x) . \end{array} $$ Then, we must have $$ m{1}(c-a)+m_{2}(b-c) \leq A \leq M_{1}(c-a)+M_{2}(b-c)
$$
Since $m \leq \min \left{m_{1}, m_{2}\right}$ and $\max \left{M_{1}, M_{2}\right} \leq M$, we have
$$
\begin{gathered}
m(b-a)=m(c-a)+m(b-c) \leq m_{1}(c-a)+m_{2}(b-c) \
M(b-a)=M(c-a)+M(b-c) \geq M_{1}(c-a)+M_{2}(b-c)
\end{gathered}
$$
Thus, we can infer that the estimates in (3.2) are better than those in (3.1). We may be able to improve these bounds by taking more and more points in $[a, b]$. This is the basic idea of Riemann integration that we describe below.
微积分代考CALCULUS代写|Lower and Upper Sums
Let $f:[a, b] \rightarrow \mathbb{R}$ be a bounded function and let $P$ be a partition of $[a, b]$, i.e., a finite set $P=\left{x_{0}, x_{1}, x_{2}, \ldots, x_{k}\right}$ of points in $[a, b]$ such that
$$
a=x_{0}<x_{1}<x_{2}<\ldots<x_{k}=b .
$$
We shall denote such partition also by $P=\left{x_{i}\right}_{i=0}^{k}$. Corresponding to the partition $P=\left{x_{i}\right}_{i=0}^{k}$ and the function $f$, we associate two numbers:
$$
L(P, f):=\sum_{i=1}^{k} m_{i}\left(x_{i}-x_{i-1}\right), \quad U(P, f):=\sum_{i=1}^{k} M_{i}\left(x_{i}-x_{i-1}\right),
$$
where
$$
m_{i}=\inf {x \in\left[x{i-1}, x_{i}\right]} f(x), \quad M_{i}=\sup {x \in\left[x{i-1}, x_{i}\right]} f(x)
$$
for $i=1, \ldots, k$.
3 Definite Integral
Note that for the definition of $L(P, f)$ and $U(P, f)$ above, we used the fact that $f$ is a bounded function (How?).
微积分代考CALCULUS代写|Some Properties of Differentiable Functions
Definition 3.1.2 Let $f:[a, b] \rightarrow \mathbb{R}$ be a bounded function. Then $f$ is said to be Riemann integrable on $[a, b]$, if there exists a unique $\gamma$ such that for every $P \in \mathcal{P}$,
$$
L(P, f) \leq \gamma \leq U(P, f)
$$
and in that case, $\gamma$ is called the Riemann integral ${ }^{1}$ of $f$, and it is denoted by
$$
\int_{a}^{b} f(x) d x
$$
CONVENTION: In the due course, Riemann integral will be simply referred to as the integral.
微积分代考CALCULUS代写|INTRODUCTION
因此,我们得到一个上限和下限一种. 为了得到更好的估计,让我们考虑一个点C这样一种<C<b. 然后我们有
米1≤F(X)≤米1∀X∈[一种,C];米2≤F(X)≤米2∀X∈[C,b]
其中
$$
\begin{array}{ll}
m_{1}=\inf {x \in[a, c]} f(x), \quad m {2}=\inf {x \in[c, b ]} f(x), \ M {1}=\sup {x \in[a, c]} f(x), \quad M {2}=\sup {x \in[c, b]} f (X) 。\结束{数组}吨H和n,在和米你s吨H一种v和m {1}(ca)+m_{2}(bc) \leq A \leq M_{1}(ca)+M_{2}(bc)
由于 $m \leq \min \left{m_{1}, m_{2}\right}$ 和 $\max \left{M_{1}, M_{2}\right} \leq M$,我们有由于 $m \leq \min \left{m_{1}, m_{2}\right}$ 和 $\max \left{M_{1}, M_{2}\right} \leq M$,我们有
米(b−一种)=米(C−一种)+米(b−C)≤米1(C−一种)+米2(b−C) 米(b−一种)=米(C−一种)+米(b−C)≥米1(C−一种)+米2(b−C)
$$
因此,我们可以推断(3.2)中的估计优于(3.1)中的估计。我们也许可以通过获取越来越多的分数来改善这些界限[一种,b]. 这就是我们下面描述的黎曼积分的基本思想。
微积分代考CALCULUS代写|LOWER AND UPPER SUMS
让F:[一种,b]→R是一个有界函数并且让磷成为一个分区[一种,b],即有限集P=\left{x_{0}, x_{1}, x_{2}, \ldots, x_{k}\right}P=\left{x_{0}, x_{1}, x_{2}, \ldots, x_{k}\right}的点数[一种,b]这样
一种=X0<X1<X2<…<X到=b.
我们也将这样的划分表示为P=\left{x_{i}\right}_{i=0}^{k}P=\left{x_{i}\right}_{i=0}^{k}. 对应分区P=\left{x_{i}\right}_{i=0}^{k}P=\left{x_{i}\right}_{i=0}^{k}和功能F,我们关联两个数字:
一世(磷,F):=∑一世=1到米一世(X一世−X一世−1),ü(磷,F):=∑一世=1到米一世(X一世−X一世−1),
其中
$$
m_{i}=\inf {x \in\left[x {i-1}, x_{i}\right]} f(x), \quad M_{i}=\sup {x \in \left[x {i-1}, x_{i}\right]} f(x)
$$
为一世=1,…,到.
3 定积分
注意对于定义一世(磷,F)和ü(磷,F)上面,我们使用了这样一个事实F是一个有界函数(如何?)。
微积分代考CALCULUS代写|SOME PROPERTIES OF DIFFERENTIABLE FUNCTIONS
定义 3.1.2 让F:[一种,b]→R是有界函数。然后F据说是黎曼可积的[一种,b], 如果存在唯一C这样对于每个磷∈磷,
一世(磷,F)≤C≤ü(磷,F)
在这种情况下,C称为黎曼积分1的F, 并表示为
∫一种bF(X)dX
约定:在适当的时候,黎曼积分将被简称为积分。

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。