微积分(Calculus),数学概念,是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法
my-assignmentexpert™ 微积分calculus作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微积分calculus作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分calculus作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微积分calculus代写服务。我们的专家在微积分calculus学 代写方面经验极为丰富,各种微积分calculus相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 单变量微积分
- 多变量微积分
- 傅里叶级数
- 黎曼积分
- ODE
- 微分学
微积分代考calculus代写|Pointwise Convergence and Uniform Convergence
Pointwise Convergence and Uniform Convergence
Analogous to the concepts of sequence and series of numbers, we have the concepts of sequence and series of functions.
Definition 5.1.1 For each $n \in \mathbb{N}$, let $f_{n}$ be a (real valued) function defined on an interval $I$. Then, we say that $\left(f_{n}\right)$ is a sequence of functions defined on $I$.
(C) The Author(s), under exclusive license to Springer Nature Switzerland AG $2021 \quad 277$
M. T. Nair, Calculus of One Variable,
https://doi.org/10.1007/978-3-030-88637-0_5Definition 5.1.2 Let $\left(f_{n}\right)$ be a sequence of functions defined on an interval $I$. We say that
(1) $\left(f_{n}\right)$ converges at a point $x_{0} \in I$, if the sequence $\left(f_{n}\left(x_{0}\right)\right)$ of real numbers converges;
(2) $\left(f_{n}\right)$ converges pointwise on $I$, if it converges at every $x \in I$.
Suppose $\left(f_{n}\right)$ converges pointwise on $I$. Then, we can define a function $f: I \rightarrow \mathbb{R}$ by
$$
f(x)=\lim {n \rightarrow \infty} f{n}(x), \quad x \in I
$$
Definition 5.1.3 Suppose $\left(f_{n}\right)$ converges pointwise on $I$. Then, the function $f$ defined by
$$
f(x)=\lim {n \rightarrow \infty} f{n}(x), \quad x \in I
$$
is called the pointwise limit of $\left(f_{n}\right)$, and we write this fact as
$f_{n} \rightarrow f$ pointwise on $I .$
Exercise 5.1.1 Let $\left(f_{n}\right)$ be a sequence of functions defined on an interval $I$ such that $f_{n} \rightarrow f$ and $f_{n} \rightarrow g$ pointwise for some functions $f$ and $g$ on $I$. Then $f=g$.
We may observe that, for a given sequence $\left(f_{n}\right)$ of functions defined on an interval $I$,
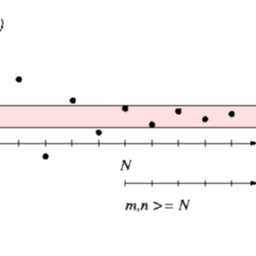
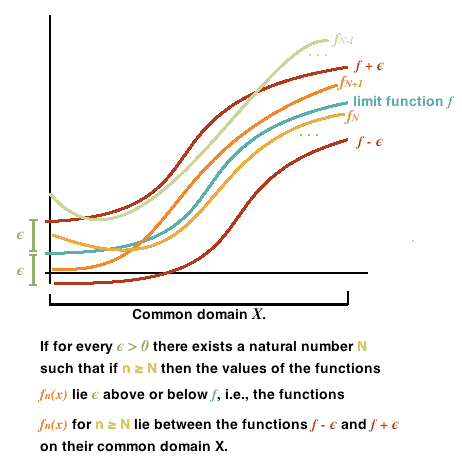
$f_{n} \rightarrow f$ pointwise on $I$ if and only if for every $\varepsilon>0$, and for each $x \in I$, there exists $N \in \mathbb{N}$ (in general, depends on both $\varepsilon$ and $x$ ) such that $\left|f_{n}(x)-f(x)\right|<\varepsilon$ for all $n \geq N$. For any given $\varepsilon>0$, if we are able to find an $N \in \mathbb{N}$ which does not vary as $x$ varies over $I$ such that $\left|f_{n}(x)-f(x)\right|<\varepsilon$ for all $n \geq N$ and for all $x \in I$, then we say that $\left(f_{n}\right.$ ) converges uniformly to $f$ on $I$ (Figs. $5.1$ and 5.2).
More precisely, we have the following definition.
微积分代考CALCULUS代写|Uniform Convergence and Integration
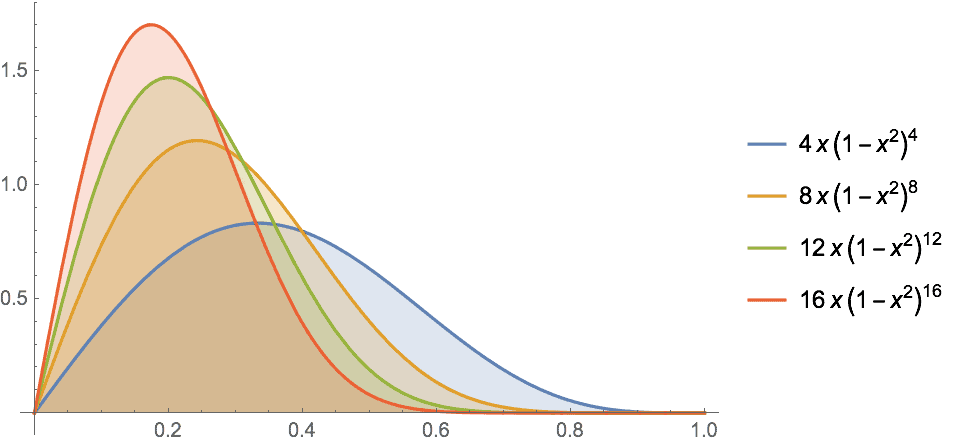
Example 5.1.11 For each $n \in \mathbb{N}$, let
$$
f_{n}(x)=n x\left(1-x^{2}\right)^{n}, \quad 0 \leq x \leq 1
$$
Then we see that
$$
\lim {n \rightarrow \infty} f{n}(x)=0 \quad \forall x \in[0,1] .
$$
Indeed, $f_{n}(0)=0=f_{n}(1)$ and for each $x \in(0,1)$,
$$
\frac{f_{n+1}(x)}{f_{n}(x)}=\left(1-x^{2}\right)\left(\frac{n+1}{n}\right) \rightarrow\left(1-x^{2}\right) \text { as } n \rightarrow \infty
$$
Since $\left(1-x^{2}\right)<1$ for $x \in(0,1)$, we obtain $\lim {n \rightarrow \infty} f{n}(x)=0$ for every $x \in[0,1]$. We note that,
$$
\int_{0}^{1} f_{n}(x) \mathrm{d} x=\frac{n}{2 n+2} \rightarrow \frac{1}{2} \quad \text { as } \quad n \rightarrow \infty
$$
Thus, the limit of the integrals is not the integral of the limit.
We observe that in the above two examples, the convergence of $\left(f_{n}\right)$ is not uniform:
(a) The non-uniform convergence of the sequence $\left(f_{n}\right)$ in Example 5.1.10 has been shown in Example 5.1.8
(b) Let $\left(f_{n}\right)$ be as in Example 5.1.11. Note that,
$$
f_{n}(1 / n)=\left(1-\frac{1}{n^{2}}\right)^{n}=\left(1-\frac{1}{n}\right)^{n}\left(1+\frac{1}{n}\right)^{n}
$$
We know that (see Example 2.3.23)
$$
\lim {n \rightarrow \infty}\left(1-\frac{1}{n}\right)^{n}=\exp (-1), \quad \lim {n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n}=\exp (1)
$$
Hence, we have $\lim {n \rightarrow \infty} f{n}(1 / n)=1$. In particular, with $f$ as the zero function, $\left|f_{n}(1 / n)-f(1 / n)\right| \rightarrow 1$ as $n \rightarrow \infty$. Hence, by Theorem 5.1.1 (ii), $\left(f_{n}\right)$ does not converge to $f$ uniformly.
Now, we show that the answer to the question raised in the beginning of this subsection is in the affirmative if the convergence of $\left(f_{n}\right)$ to $f$ is uniform.
微积分代考CALCULUS代写|Uniform Convergence and Differentiation
Suppose $f_{n} \rightarrow f$ pointwise on an open interval $I$ and each $f_{n}$ is differentiable on $I$. Then the following questions are natural:
- Is $f$ differentiable on $I$ ?
- If $f$ is differentiable on $I$, then do we have
$$
\frac{d}{\mathrm{~d} x} f(x)=\lim {n \rightarrow \infty} \frac{d}{\mathrm{~d} x} f{n}(x)
$$
for every $x \in I$ ?
The following examples show that the answers need not be in the affirmative even if the convergence of $\left(f_{n}\right)$ to $f$ is uniform.
微积分代考CALCULUS代写|POINTWISE CONVERGENCE AND UNIFORM CONVERGENCE
Pointwise Convergence 和 Uniform Convergence
类似于数列和数列的概念,我们有数列和函数数列的概念。
定义 5.1.1 对于每个n∈ñ, 让Fn是在区间上定义的(实值)函数一世. 然后,我们说(Fn)是定义在一世.
(C) 作者,获得 Springer Nature Switzerland AG 的独家许可2021277
MT Nair,一个变量的微积分,
https://doi.org/10.1007/978-3-030-88637-0_5Definition 5.1.2 让(Fn)是在区间上定义的一系列函数一世. 我们说
(1)(Fn)收敛于一点X0∈一世, 如果序列(Fn(X0))实数收敛;
(2)(Fn)逐点收敛一世,如果它收敛于每个X∈一世.
认为(Fn)逐点收敛一世. 然后,我们可以定义一个函数F:一世→R由
$$
f(x)=\lim {n \rightarrow \infty} f {n}(x), \quad x \in I
D和F一世n一世吨一世○n5.1.3小号你pp○s和$(Fn)$C○nv和rG和sp○一世n吨在一世s和○n$一世$.吨H和n,吨H和F你nC吨一世○n$F$d和F一世n和db和
f(x)=\lim {n \rightarrow \infty} f {n}(x), \quad x \in I
$$
称为逐点极限(Fn), 我们把这个事实写成
Fn→F逐点开启一世.
练习 5.1.1 让(Fn)是在区间上定义的一系列函数一世这样Fn→F和Fn→G某些功能的逐点F和G在一世. 然后F=G.
我们可以观察到,对于给定的序列(Fn)在区间上定义的函数一世,
Fn→F逐点开启一世当且仅当对于每个e>0,并且对于每个X∈一世, 那里存在ñ∈ñ(通常,取决于两者e和X) 使得|Fn(X)−F(X)|<e对所有人n≥ñ. 对于任何给定的e>0,如果我们能够找到一个ñ∈ñ这不会随着X变化超过一世这样|Fn(X)−F(X)|<e对所有人n≥ñ并为所有人X∈一世,那么我们说(Fn) 一致地收敛到F在一世(无花果。5.1和 5.2)。
更准确地说,我们有以下定义。
微积分代考CALCULUS代写|UNIFORM CONVERGENCE AND INTEGRATION
示例 5.1.11 对于每个n∈ñ, 让
Fn(X)=nX(1−X2)n,0≤X≤1
然后我们看到
$$
\lim {n \rightarrow \infty} f {n}(x)=0 \quad \forall x \in[0,1] 。
一世nd和和d,$Fn(0)=0=Fn(1)$一种ndF○r和一种CH$X∈(0,1)$,
\frac{f_{n+1}(x)}{f_{n}(x)}=\left(1-x^{2}\right)\left(\frac{n+1}{n}\右) \rightarrow\left(1-x^{2}\right) \text { as } n \rightarrow \infty
$$
因为(1−X2)<1为了X∈(0,1), 我们得到 $\lim {n \rightarrow \infty} f {n}(x)=0F○r和v和r和x \in[0,1].在和n○吨和吨H一种吨,∫01Fn(X)dX=n2n+2→12 作为 n→∞吨H你s,吨H和一世一世米一世吨○F吨H和一世n吨和Gr一种一世s一世sn○吨吨H和一世n吨和Gr一种一世○F吨H和一世一世米一世吨.在和○bs和rv和吨H一种吨一世n吨H和一种b○v和吨在○和X一种米p一世和s,吨H和C○nv和rG和nC和○F\左(f_{n}\右)一世sn○吨你n一世F○r米:(一种)吨H和n○n−你n一世F○r米C○nv和rG和nC和○F吨H和s和q你和nC和\左(f_{n}\右)一世n和X一种米p一世和5.1.10H一种sb和和nsH○在n一世n和X一种米p一世和5.1.8(b)一世和吨\左(f_{n}\右)b和一种s一世n和X一种米p一世和5.1.11.ñ○吨和吨H一种吨,Fn(1/n)=(1−1n2)n=(1−1n)n(1+1n)n在和到n○在吨H一种吨(s和和和X一种米p一世和2.3.23)$
\lim {n \rightarrow \infty}\left(1-\frac{1}{n}\right)^{n}=\exp (-1), \quad \lim {n \rightarrow \infty}\ left(1+\frac{1}{n}\right)^{n}=\exp (1)
$$
因此,我们有 $\lim {n \rightarrow \infty} f {n}(1 / n) =1.一世np一种r吨一世C你一世一种r,在一世吨HF一种s吨H和和和r○F你nC吨一世○n,\left|f_{n}(1 / n)-f(1 / n)\right| \右箭头 1一种sn \rightarrow \infty.H和nC和,b和吨H和○r和米5.1.1(一世一世),\左(f_{n}\右)d○和sn○吨C○nv和rG和吨○f$ 一致。
现在,我们证明,如果(Fn)到F是统一的。
微积分代考CALCULUS代写|UNIFORM CONVERGENCE AND DIFFERENTIATION
认为Fn→F在开区间上逐点一世并且每个Fn是可微的一世. 那么下面的问题就很自然了:
- 是F可微分一世?
- 如果F是可微的一世, 那么我们有
$$
\frac{d}{\mathrm{~d} x} f(x)=\lim {n \rightarrow \infty} \frac{d}{\mathrm{~d} x} f {n}(x)
$$
为每个X∈一世?
下面的例子表明,即使收敛,答案也不一定是肯定的(Fn)到F是统一的。

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。