如果你也在 怎样代写量子计算Quantum computing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。量子计算Quantum computing是物理和计算机的交叉学科,构造新型计算模式。传统计算机和量子计算机之间的根本区别在于,量子计算机中的程序本质上是概率性质的,而传统计算机通常是确定性的。 在量子算法中,每个可能的结果都有关联的概率振幅。 测量后,其中某个可能状态以特定概率获得。 该情况与传统计算相反,在传统计算中,一个位只能是确定的 0 或 1。
量子计算是一种遵循量子力学规律调控量子信息单元进行计算的新型计算模式。 对照于传统的通用计算机,其理论模型是通用图灵机;通用的量子计算机,其理论模型是用量子力学规律重新诠释的通用图灵机。
量子计算Quantum computation领域盛行的量子计算模型是以量子逻辑门的网络来描述计算的。这个模型是布尔电路的一个复杂的线性代数的概括。
一个由$n$位信息组成的存储器有$2^{n}$的可能状态。因此,代表所有存储器状态的向量有2^{n}$项(每个状态一个)。这个向量被看作是一个概率向量,代表内存在某个特定状态下被发现的事实。
在经典观点中,一个条目的值为1(即处于这种状态的概率为100美元),所有其他条目都是0。
在量子力学中,概率向量可以被概括为密度算子。量子状态向量形式主义通常首先被介绍,因为它在概念上更简单,而且它可以代替密度矩阵形式主义用于纯状态,在那里整个量子系统是已知的。
我们首先考虑一个只由一个比特组成的简单存储器。这个存储器可以在两种状态中找到一个:零状态或一状态。我们可以用狄拉克符号来表示这个存储器的状态,因此
$|0\rangle:=\left(\begin{array}{l}1 \ 0\end{array}\right)$
$|1\rangle:=\left(\begin{array}{l}0 \ 1\end{array}\right)$
然后,在两个经典状态$|0\rangle$和$|1\rangle$的任何量子叠加中可以找到一个量子存储器。
$|\psi\rangle:=\alpha|0\rangle+\beta|1\rangle=\left(\begin{array}{c}\alpha \ \beta\end{array}\right) ; \quad|\alpha|^{2}+|\beta|^{2}=1$
my-assignmentexpert™ 量子计算Quantum computing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的量子计算Quantum computing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此量子计算Quantum computing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在统计Statistics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计Statistics代写服务。我们的专家在量子计算Quantum computing代写方面经验极为丰富,各种量子计算Quantum computing相关的作业也就用不着 说。
我们提供的量子计算Quantum computing及其相关学科的代写,服务范围广, 其中包括但不限于:
- 密码学 Cryptography
- 搜索算法 Search problems
- 量子系统的仿真 Simulation of quantum systems
- 机器学习 Machine learning
- 计算生物学 Computational biology
- Computer-aided drug design and generative chemistry
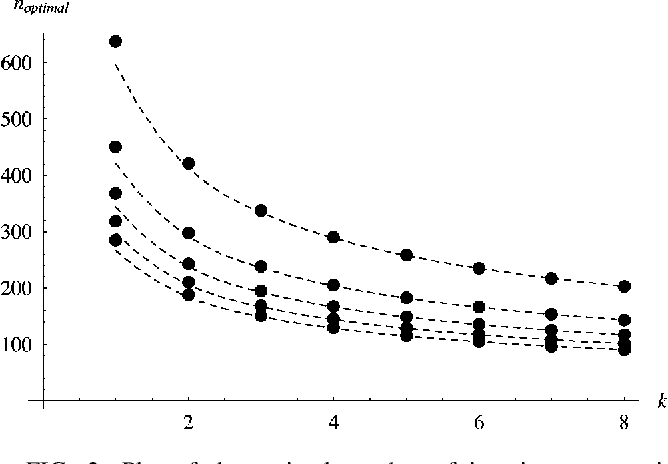
Amplitude amplification can be applied to more general classes of search problems in which a multiplicity of solutions may exist. In the case of $k$ solutions, Grover’s algorithm can find one solution in $O\left((N / k)^{1 / 2}\right)$ time – but only if the value of $k$ is known. The need for the value of $k$ can be seen from the formula for determining the number of iterations.
Indeed, after $r$ iterations of the Grover operator the superposition with $k$ solutions will look like:
$$
|\Psi(r)\rangle=\alpha(r) \sum_{n o n-\text { solutions }}|\boldsymbol{x}\rangle+\beta(r) \sum_{\text {solutions }}|\boldsymbol{y}\rangle
$$
which normalization looks like:
$$
|\alpha(r)|^{2}(N-k)+|\beta(r)|^{2} k=1
$$
This suggests the parametrization given by:
$$
\begin{aligned}
|\alpha(r)|^{2}(N-k) &=\cos ^{2}(2 r+1) \theta \
|\beta(r)|^{2} k &=\sin ^{2}(2 r+1) \theta
\end{aligned}
$$
and therefore:
$$
\begin{aligned}
&\beta(r)=\frac{1}{\sqrt{k}} \sin (2 r+1) \theta \
&\alpha(r)=\frac{1}{\sqrt{N-k}} \cos (2 r+1) \theta
\end{aligned}
$$
with:
$$
\sin \theta=\sqrt{\frac{k}{N}}
$$
A before, high probability of measuring a solution implies:
$$
\begin{aligned}
&\beta(r) \approx 1 \sqrt{k} \
&\alpha(r) \approx 0
\end{aligned}
$$
And for large $N \gg k$ :
$$
\sin \theta=\sqrt{\frac{k}{N}} \ll 1 \Rightarrow \sin \theta \approx \theta \Rightarrow \theta \approx \sqrt{\frac{k}{N}}
$$
Therefore:
$$
(2 r+1) \theta \approx \frac{\pi}{2} \Rightarrow r \approx \frac{\pi}{4} \sqrt{\frac{N}{k}}-\frac{1}{2}
$$
As a consequence, for large $N$, the probability is maximized with $r \approx(\pi / 4) \sqrt{N / k}$ iterations, which implies that $O\left((N / k)^{1 / 2}\right)$ Grover iterations are required.
In most practical applications $k$ is unknown, which means that Grover’s algorithm cannot be applied. It is possible to apply a quantum counting algorithm to determine the number of solutions. An optimal quantum counting algorithm has complexity $O\left((k N)^{1 / 2}\right)$, which would dominate the search complexity [10]. Fortunately, a different formulation of the amplitude amplification procedure can be applied to find a solution in $O\left((N / k)^{1 / 2}\right)$ time, even if $k$ is unknown [9].
The fact that a solution can be found more efficiently, as $k$ gets large, should be no surprise: as the number of solutions increases, the probability of sampling one of them increases. For example, if $k=O(N)$ we can find a solution in $O(1)$ time, just from random sampling. $O\left((N / k)^{1 / 2}\right)$ is provably optimal for this type of search problem; however, most practical applications require retrieval of all $k$ solutions, not one of them chosen at random.
However, we cannot output the entire solution dataset using a single application of Grover’s algorithm. Indeed, the superposition of states for the last iteration of Grover’s algorithm, with known $k$, looks like:
$$
\left|\boldsymbol{Q}{\boldsymbol{A}}\right\rangle=G^{r}|\boldsymbol{\Psi}(\mathbf{0})\rangle \approx \sin ((2 r+1) \theta) \frac{1}{\sqrt{k}} \sum{\text {solutions }}|\boldsymbol{y}\rangle
$$
where the probability of finding a nonsolution is presumed to be small and has been neglected in the equation. Thus, $\left|\boldsymbol{Q}_{\boldsymbol{A}}\right\rangle$ is very close to be a superposition of solution states.
Unfortunately, a measurement to retrieve a solution causes the superposition to collapse, thus, losing all information relating to other possible solution states.
We could apply Grover’s algorithm multiple times to retrieve the entire dataset of solutions. But to do so, we require about $O(k \log (k))$ applications of Grover’s algorithm, and the overall complexity of the solution is $O(\sqrt{k N} \log (k))$. For a dense dataset, where $k$ is comparable to $N$, the complexity is reduced to $O(N \log (N))$. This is a suboptimal solution, as the brute force classical search leads to an improved complexity of $O(N)$.
物理代写
物理代考
幅度放大可以应用于可能存在多种解决方案的更一般类别的搜索问题。如果是到解,Grover 算法可以在○((ñ/到)1/2)时间——但前提是到是已知的。对价值的需求到从确定迭代次数的公式可以看出。
确实,之后rGrover 算子的迭代与到解决方案将如下所示:
|Ψ(r)⟩=一种(r)∑n○n− 解决方案 |X⟩+b(r)∑解决方案 |和⟩
标准化看起来像:
|一种(r)|2(ñ−到)+|b(r)|2到=1
这表明由下式给出的参数化:
|一种(r)|2(ñ−到)=某物2(2r+1)θ |b(r)|2到=没有2(2r+1)θ
因此:
b(r)=1到没有(2r+1)θ 一种(r)=1ñ−到某物(2r+1)θ
和:
没有θ=到ñ
以前,测量解决方案的高概率意味着:
b(r)≈1到 一种(r)≈0
而对于大ñ≫到:
没有θ=到ñ≪1⇒没有θ≈θ⇒θ≈到ñ
所以:
(2r+1)θ≈圆周率2⇒r≈圆周率4ñ到−12
因此,对于大ñ,概率最大化r≈(圆周率/4)ñ/到迭代,这意味着○((ñ/到)1/2)需要 Grover 迭代。
在大多数实际应用中到是未知的,这意味着不能应用格罗弗算法。可以应用量子计数算法来确定解的数量。最优量子计数算法具有复杂性○((到ñ)1/2),这将主导搜索复杂性10. 幸运的是,可以应用不同的幅度放大程序公式来找到解决方案○((ñ/到)1/2)时间,即使到未知9.
可以更有效地找到解决方案的事实,如到变大,应该不足为奇:随着解决方案数量的增加,对其中一个进行采样的概率也会增加。例如,如果到=○(ñ)我们可以在○(1)时间,只是来自随机抽样。○((ñ/到)1/2)可证明对于此类搜索问题是最优的;然而,大多数实际应用需要检索所有到解决方案,而不是随机选择的解决方案之一。
但是,我们无法使用 Grover 算法的单个应用程序输出整个解决方案数据集。事实上,Grover 算法最后一次迭代的状态叠加,已知到, 看起来像:
$$
\left|\boldsymbol{Q} {\boldsymbol{A}}\right\rangle=G^{r}|\boldsymbol{\Psi}0\rangle \大约 \sin(2r+1\theta) \frac{1}{\sqrt{k}} \sum {\text {solutions }}|\boldsymbol{y}\rangle
$$
其中假定找到非解的概率很小并且被忽略了在等式中。因此,|问一种⟩非常接近于解态的叠加。
不幸的是,检索解决方案的测量会导致叠加崩溃,从而丢失与其他可能的解决方案状态相关的所有信息。
我们可以多次应用 Grover 算法来检索整个解决方案数据集。但要做到这一点,我们需要大约○(到日志(到))Grover 算法的应用,解的整体复杂度为○(到ñ日志(到)). 对于密集数据集,其中到相当于ñ, 复杂度降低到○(ñ日志(ñ)). 这是一个次优的解决方案,因为蛮力经典搜索导致改进的复杂性○(ñ).

物理代写| 量子计算作业代写Quantum computing代考|UNDERSTANDING QUANTUM ALGORITHMICS 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。