如果你也在 怎样统计计算Statistical Computing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计计算Statistical Computing是统计学和计算机科学之间的纽带。它意味着通过使用计算方法来实现的统计方法。它是统计学的数学科学所特有的计算科学(或科学计算)的领域。这一领域也在迅速发展,导致人们呼吁应将更广泛的计算概念作为普通统计教育的一部分。与传统统计学一样,其目标是将原始数据转化为知识,[2]但重点在于计算机密集型统计方法,例如具有非常大的样本量和非同质数据集的情况。
许多统计建模和数据分析技术可能难以掌握和应用,因此往往需要使用计算机软件来帮助实施大型数据集并获得有用的结果。S-Plus是公认的最强大和最灵活的统计软件包之一,它使用户能够应用许多统计方法,从简单的回归到时间序列或多变量分析。该文本广泛涵盖了许多基本的和更高级的统计方法,集中于图形检查,并具有逐步说明的特点,以帮助非统计学家充分理解方法。
my-assignmentexpert™统计计算Statistical Computing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计计算Statistical Computing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计计算Statistical Computing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在统计计算Statistical Computing作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的统计计算Statistical Computing代写服务。我们的专家在统计计算Statistical Computing代写方面经验极为丰富,各种统计计算Statistical Computing相关的作业也就用不着 说。
我们提供的统计计算Statistical Computing及其相关学科的代写,服务范围广, 其中包括但不限于:
- 随机微积分 Stochastic calculus
- 随机分析 Stochastic analysis
- 随机控制理论 Stochastic control theory
- 微观经济学 Microeconomics
- 数量经济学 Quantitative Economics
- 宏观经济学 Macroeconomics
- 经济统计学 Economic Statistics
- 经济学理论 Economic Theory
- 计量经济学 Econometrics
统计代写
数学代写|统计计算作业代写Statistical Computing代考|Description of the method
Due to the complex structure of the state space used in RJMCMC methods, more mathematical formalism is required to state the RJMCMC algorithm than was necessary in the previous sections. This section introduces the required notation and states the general RJMCMC algorithm.
We start the exposition by giving a mathematical description of the state space: Let $I$ be a finite or countable set and let $d_{k} \in \mathbb{N}{0}$ for all $k \in I$ be given. Define $$ S{k}={k} \times \mathbb{R}^{d_{k}}
$$
for all $k \in I$ and
$$
S=\bigcup_{k \in I} S_{k}
$$
Then the elements $z$ of the space $S$ have the form $z=(k, x)$, where $x \in \mathbb{R}^{d_{k}}$ and $k \in I$. Since the index $k$ is included as the first component of all elements in $S_{k}$, the spaces $S_{k}$ are disjoint and each $z \in S$ is contained in exactly one of the subspaces $S_{k}$. For a value $(k, x) \in S$, the first component, $k$, indicates which of the spaces $\mathbb{R}^{d_{k}}$ a point is in while the second component, $x$, gives the position in this space. The space $S$ is the state space our target distribution will live on and the Markov chain constructed by the RJMCMC algorithm will move in.
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|Bayesian inference for mixture distributions
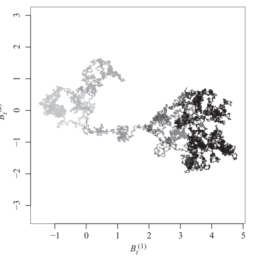
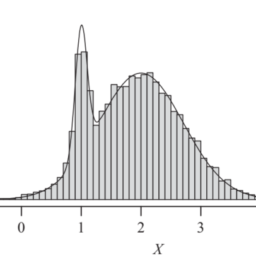
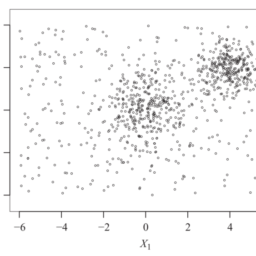
In this section we illustrate the RJMCMC algorithm $4.36$ with the help of an example: we consider a Bayesian inference problem for mixture distributions. For the example, we assume the following model: observations $Y_{1}, \ldots, Y_{n}$ are given from a twodimensional mixture distribution
$$
\mu=\frac{1}{k} \sum_{a=1}^{k} \mathcal{N}\left(\mu_{a}, r_{a}^{2} I_{2}\right),
$$
where $I_{2}$ is the two-dimensional identity matrix. We assume that the number $k$ of modes, the means $\mu_{a}$ and the standard deviations $r_{a}$ are all random, with distributions given by
$$
k \sim \operatorname{Pois}(3)+1
$$
as well as
$$
\mu_{a} \sim \mathcal{U}([-10,+10] \times[-10,+10])
$$
and
$$
r_{a} \sim \mathcal{U}\left[\frac{1}{2}, \frac{5}{2}\right]
$$
for all $a \in{1, \ldots, k}$. Our aim is to generate samples from the posterior distribution of $k, \mu_{a}$ and $r_{a}$, given the data $Y_{1}, \ldots, Y_{n}$.
In this section we will use the RJMCMC algorithm to generate the required samples. In order to do so we first have to determine the state space $S$ and the target distribution on this state space, and then we have to choose a set of moves which allows the algorithm to efficiently explore all of the state space.
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|DESCRIPTION OF THE METHOD
由于 RJMCMC 方法中使用的状态空间结构复杂,因此需要更多的数学形式来说明 RJMCMC 算法,而不是前面章节中所需要的。本节介绍所需的符号并说明通用 RJMCMC 算法。
我们首先给出状态空间的数学描述:让一世是一个有限集或可数集,令 $d_{k} \in \mathbb{N} {0}F○r一种一世一世k \in 我b和G一世v和n.D和F一世n和$ S {k}={k} \times \mathbb{R}^{d_{k}}
F○r一种一世一世$到∈一世$一种nd
S=\bigcup_{k \in I} S_{k}
$$
然后是元素和空间的小号有表格和=(到,X), 在哪里X∈Rd到和到∈一世. 由于指数到被作为所有元素的第一个组件包含在小号到, 空间小号到是不相交的并且每个和∈小号恰好包含在其中一个子空间中小号到. 对于一个值(到,X)∈小号,第一个组件,到, 表示哪个空格Rd到一个点在,而第二个组件,X,给出在这个空间中的位置。空间小号是我们的目标分布将存在的状态空间,由 RJMCMC 算法构建的马尔可夫链将进入。
数学代写|统计计算作业代写STATISTICAL COMPUTING代考|BAYESIAN INFERENCE FOR MIXTURE DISTRIBUTIONS
在本节中,我们将说明 RJMCMC 算法4.36借助示例:我们考虑混合分布的贝叶斯推理问题。例如,我们假设以下模型:观察和1,…,和n由二维混合分布给出
μ=1到∑一种=1到ñ(μ一种,r一种2一世2),
在哪里一世2是二维单位矩阵。我们假设数到模式,手段μ一种和标准差r一种都是随机的,分布由
到∼因为(3)+1
也
μ一种∼ü([−10,+10]×[−10,+10])
和
r一种∼ü[12,52]
对所有人一种∈1,…,到. 我们的目标是从后验分布中生成样本到,μ一种和r一种,给定数据和1,…,和n.
在本节中,我们将使用 RJMCMC 算法生成所需的样本。为此,我们首先必须确定状态空间小号以及该状态空间上的目标分布,然后我们必须选择一组移动,使算法能够有效地探索所有状态空间。

计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写