如果你也在 怎样代写实分析real analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。实分析real analysis是数学分析的一个分支,研究实数、实数序列和实数函数的行为。 实分析研究的实值序列和函数的一些特殊性质包括收敛性、极限、连续性、平稳性、可微分性和可整定性。实分析有别于复分析,后者涉及复数及其函数的研究。
实分析real analysis是数学中的一个经典分支,它的发展是为了使数和函数的研究正规化,并研究重要的概念,如极限和连续性。这些概念是微积分及其应用的基础。实物分析已经成为许多应用领域中不可或缺的工具。
实分析real analysis的基础知识:序列和数列的收敛性、连续性、可分性、黎曼积分、函数的序列和数列、均匀性以及极限操作的互换。
my-assignmentexpert™ 实分析real analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的实分析real analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复分析complex analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学mathematics代写服务。我们的专家在实分析real analysis代写方面经验极为丰富,各种实分析real analysis相关的作业也就用不着 说。
我们提供的实分析real analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|实分析代写real analysis代考|Extended Real-Valued Functions
We begin with extended real-valued functions. A generic measurable, extended real-valued function $f$ can take both positive and negative values, so to define its integral we split $f$ into its positive and negative parts $f^{+}(x)=\max {f(x), 0}$ and $f^{-}(x)=\max {-f(x), 0}$. Since $f^{+}$and $f^{-}$are nonnegative and measurable, they each have well-defined Lebesgue integrals. Furthermore, $f=f^{+}-f^{-}$, so we will declare the integral of $f$ to be the difference of $\int_{E} f^{+}$and $\int_{E} f^{-}$. However, we must be careful to exclude any cases that would assign an indeterminate form to the integral.
Definition 4.3.1 (Lebesgue Integral of an Extended Real-Valued Function). Let $f: E \rightarrow[-\infty, \infty]$ be a measurable extended real-valued function defined on a measurable set $E \subseteq \mathbb{R}^{d}$. The Lebesgue integral of $f$ over $E$ is
$$
\int_{E} f=\int_{E} f^{+}-\int_{E} f^{-},
$$
as long as this does not have the form $\infty-\infty$ (in that case, the integral is undefined).
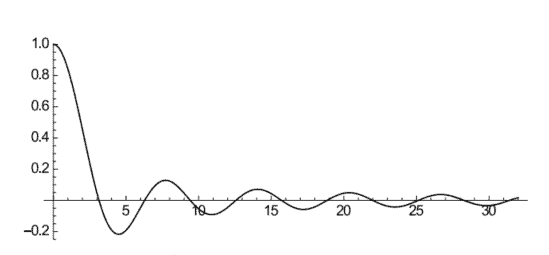
Here is an example of a function whose Lebesgue integral does not exist.
数学代写|实分析代写REAL ANALYSIS代考|Complex-Valued Functions
4.3.2 Complex-Valued Functions
Now we turn to the complex-valued setting. We define the integral of a complex-valued function by breaking it into real and imaginary parts.
Definition 4.3.4 (Lebesgue Integral of a Complex-Valued Function). Let $f: E \rightarrow \mathbb{C}$ be a measurable complex-valued function defined on a measurable set $E \subseteq \mathbb{R}^{d}$. Write $f$ in real and imaginary parts as $f=f_{r}+i f_{i}$, where $f_{r}$ and $f_{i}$ are real-valued. If $\int_{E} f_{r}$ and $\int_{E} f_{i}$ both exist and are finite, then the Lebesgue integral of $f$ over $E$ is
$$
\int_{E} f=\int_{E} f_{r}+i \int_{E} f_{i}
$$
Otherwise, the integral is undefined. $\diamond$
While the integral of an extended real-valued function can be $\pm \infty$, the integral of a complex-valued function is always a complex scalar (if it exists).
Now we derive an analogue of Lemma $4.3 .3$ for complex-valued functions.
数学代写|实分析代写REAL ANALYSIS代考|Properties of the Integral
The following exercise gives some properties of the integrals of extended realvalued or complex-valued functions. In the statement of this exercise, when we write a condition like ” $f \leq g$ a.e.” we implicitly assume that $f$ and $g$ are extended real-valued functions. However, a hypothesis such as ” $f=0$ a.e.” can be satisfied by either an extended real-valued or a complex-valued function.
Exercise 4.3.6. Let $E \subseteq \mathbb{R}^{d}$ be measurable, and assume that $f, g: E \rightarrow \overline{\mathbf{F}}$ are measurable. Prove the following statements.
(a) If $\int_{E} f$ and $\int_{E} g$ both exist and $f \leq g$ a.e., then $\int_{E} f \leq \int_{E} g$.
(b) If $\int_{E} f$ and $\int_{E} g$ both exist and $f=g$ a.e., then $\int_{E} f=\int_{E} g$.
(c) If $\int_{E} f$ exists and $A$ is a measurable subset of $E$, then $\int_{A} f$ exists.
(d) If $f=0$ a.e. on $E$, then $\int_{E} f$ exists and $\int_{E} f=0$.
(e) If $\int_{E} f$ exists and $c$ is a scalar, then $\int_{E} c f$ exists and $\int_{E} c f=c \int_{E} f$.
(f) If $\int_{E} f$ exists and $A_{1}, A_{2}, \ldots$ are disjoint measurable subsets of $E$, then
(g) If $\int_{E} f$ exists and $A_{1} \subseteq A_{2} \subseteq \cdots$ are nested measurable subsets of $E$, then
$$
\int_{\cup A_{n}} f=\lim {n \rightarrow \infty} \int{A_{n}} f .
$$
In particular, statement (b) of the preceding exercise shows that changing the value of a function on a set of zero measure does not change the value of its integral. Consequently, many of our earlier theorems that required hypotheses to hold at all points are still valid if we assume only that the hypotheses hold almost everywhere. Here is such a version of the Monotone Convergence Theorem.
实分析代写
数学代写|实分析代写REAL ANALYSIS代考|EXTENDED REAL-VALUED FUNCTIONS
我们从扩展的实值函数开始。一个通用的可测量的、扩展的实值函数F可以取正值和负值,所以要定义它的积分,我们拆分F分为积极和消极的部分F+(X)=最大限度F(X),0和F−(X)=最大限度−F(X),0. 自从F+和F−是非负且可测量的,它们每个都有明确定义的 Lebesgue 积分。此外,F=F+−F−,所以我们将声明积分F成为∫和F+和∫和F−. 但是,我们必须小心排除任何会给积分分配不确定形式的情况。
定义 4.3.1大号和b和sG你和一世n吨和Gr一种一世这F一种n和X吨和nd和dR和一种一世−五一种一世你和dF你nC吨一世这n. 让F:和→[−∞,∞]是定义在可测集上的可测扩展实值函数和⊆Rd. 的勒贝格积分F超过和是
∫和F=∫和F+−∫和F−,
只要这没有表格∞−∞ 一世n吨H一种吨C一种s和,吨H和一世n吨和Gr一种一世一世s你nd和F一世n和d.
这是一个 Lebesgue 积分不存在的函数示例。
数学代写|实分析代写REAL ANALYSIS代考|COMPLEX-VALUED FUNCTIONS
4.3.2 复值函数
现在我们转向复值设置。我们通过将复值函数分解为实部和虚部来定义它的积分。
定义 4.3.4大号和b和sG你和一世n吨和Gr一种一世这F一种C这米p一世和X−五一种一世你和dF你nC吨一世这n. 让F:和→C是定义在可测集上的可测复值函数和⊆Rd. 写F在实部和虚部中F=Fr+一世F一世, 在哪里Fr和F一世是实值的。如果∫和Fr和∫和F一世都存在且是有限的,则 Lebesgue 积分F超过和是
∫和F=∫和Fr+一世∫和F一世
否则,积分是未定义的。⋄
而扩展实值函数的积分可以是±∞, 复值函数的积分始终是复标量一世F一世吨和X一世s吨s.
现在我们推导出引理的类似物4.3.3对于复值函数。
数学代写|实分析代写REAL ANALYSIS代考|PROPERTIES OF THE INTEGRAL
下面的练习给出了扩展实值或复值函数的积分的一些性质。在这个练习的陈述中,当我们写一个像“F≤Gae”我们隐含地假设F和G是扩展的实值函数。然而,诸如“F=0ae”可以通过扩展实值或复值函数来满足。
练习 4.3.6。让和⊆Rd是可测量的,并假设F,G:和→F¯是可测量的。证明下列陈述。
一种如果∫和F和∫和G两者都存在并且F≤Gae,那么∫和F≤∫和G.
b如果∫和F和∫和G两者都存在并且F=Gae,那么∫和F=∫和G.
C如果∫和F存在并且一种是可测量的子集和, 然后∫一种F存在。
d如果F=0啊十和, 然后∫和F存在并且∫和F=0.
和如果∫和F存在并且C是一个标量,那么∫和CF存在并且∫和CF=C∫和F.
F如果∫和F存在并且一种1,一种2,…是不相交的可测量子集和, 然后
G如果∫和F存在并且一种1⊆一种2⊆⋯是嵌套的可测量子集和,然后
$$
\int_{\cup A_{n}} f=\lim {n \rightarrow \infty} \int {A_{n}} f 。
$$
特别是声明b前面的练习表明,在一组零测度上改变函数的值不会改变它的积分值。因此,如果我们只假设假设几乎在任何地方都成立,那么我们早期要求假设在所有点都成立的许多定理仍然有效。这是单调收敛定理的一个版本。

数学代写|实分析代写real analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
离散数学代写
Partial Differential Equations代写可以参考一份偏微分方程midterm答案解析