如果你也在 怎样代写实分析real analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。实分析real analysis是数学分析的一个分支,研究实数、实数序列和实数函数的行为。 实分析研究的实值序列和函数的一些特殊性质包括收敛性、极限、连续性、平稳性、可微分性和可整定性。实分析有别于复分析,后者涉及复数及其函数的研究。
实分析real analysis是数学中的一个经典分支,它的发展是为了使数和函数的研究正规化,并研究重要的概念,如极限和连续性。这些概念是微积分及其应用的基础。实物分析已经成为许多应用领域中不可或缺的工具。
实分析real analysis的基础知识:序列和数列的收敛性、连续性、可分性、黎曼积分、函数的序列和数列、均匀性以及极限操作的互换。
my-assignmentexpert™ 实分析real analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的实分析real analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复分析complex analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学mathematics代写服务。我们的专家在实分析real analysis代写方面经验极为丰富,各种实分析real analysis相关的作业也就用不着 说。
我们提供的实分析real analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|实分析代写real analysis代考|Approximate Identity
An approximate identity or summability kernel on $\mathbb{R}$ is a family $\left{k_{N}\right}_{N \in \mathbb{N}}$ of functions in $L^{1}(\mathbb{R})$ such that the following three conditions are satisfied.
(a) $L^{1}$-normalization: $\int_{-\infty}^{\infty} k_{N}(x) d x=1$ for every $N$.
(b) $L^{1}$-boundedness: sup $\left|k_{N}\right|_{1}=\sup \int_{-\infty}^{\infty}\left|k_{N}(x)\right| d x<\infty$. (c) $L^{1}$-concentration: For every $\delta>0$,
$$
\lim {N \rightarrow \infty} \int{|x| \geq \delta}\left|k_{N}(x)\right| d x=0 .
$$
Property (a) of this definition says that each function $k_{N}$ has the same total “signed mass” in the sense that its integral is 1 , and property (c) says that most of this mass is being squeezed into smaller and smaller intervals around the origin as $N$ increases. Property (b) requires the “absolute mass” of $k_{N}$ to be bounded independently of $N$. If $k_{N} \geq 0$ for every $N$, then property (a) implies that $\left|k_{N}\right|_{1}=1$ for every $N$, so property (b) is automatically satisfied in this case.
The next exercise describes the “easy” way to construct an approximate identity: Simply choose any integrable function $k$ whose integral is 1 , and then dilate $k$ appropriately to create $k_{N}$.
数学代写|实分析代写REAL ANALYSIS代考|THE FEJ´ER KERNEL
The Fejér function is
$$
w(x)=\left(\frac{\sin \pi x}{\pi x}\right)^{2}
$$
and the Fejér kernel is $\left{w_{N}\right}_{N \in \mathbb{N}}$ where $w_{N}(x)=N w(N x)$. Prove that $w$ is integrable and $\int w=1$. Conclude that the Fejér kernel is an approximate identity.
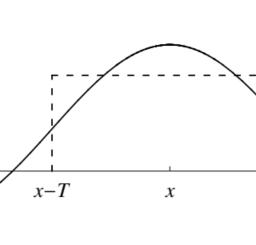
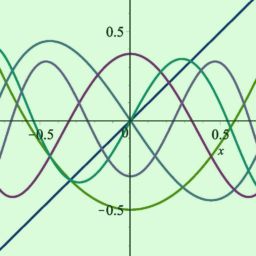
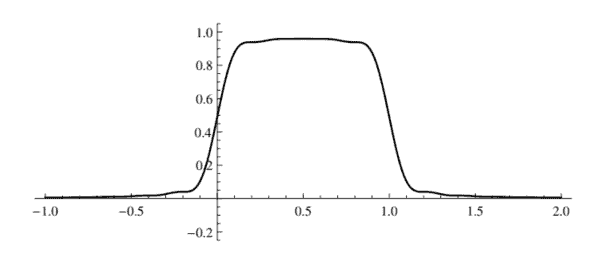
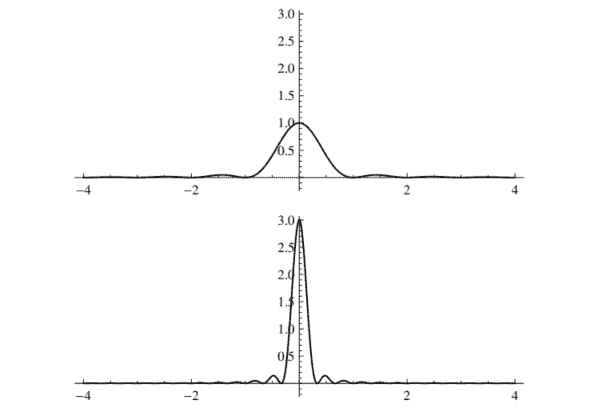
The letter ” $w$ ” is for “Weiss,” which was Fejér’s surname at birth. Plots of $w$ and $w_{3}$ appears in Figure $9.3$. We can see in that figure that $w_{N}$ becomes more spike-like as $N$ increases, just as $\chi_{T}$ becomes more spike-like as $T \rightarrow 0$.
Now we prove our claim that if $\left{k_{N}\right}_{N \in \mathbb{N}}$ is an approximate identity, then $f * k_{N} \rightarrow f$ in $L^{1}$-norm for every function $f \in L^{1}(\mathbb{R})$. The proof of this theorem illustrates two “standard tricks.” First, we introduce $k_{N}$ into one term of the computation by using the fact that $\int k_{N}=1$. Second, we divide the domain of integration into small and large parts in order to make use of the $L^{1}$-concentration property of an approximate identity.
实分析代写
数学代写|实分析代写REAL ANALYSIS代考|APPROXIMATE IDENTITY
上的近似恒等或可和性核R是一个家庭\left{k_{N}\right}_{N \in \mathbb{N}}\left{k_{N}\right}_{N \in \mathbb{N}}中的功能大号1(R)从而满足以下三个条件。
一种 大号1-正常化:∫−∞∞到ñ(X)dX=1对于每个ñ.
b 大号1-有界性:sup|到ñ|1=支持∫−∞∞|到ñ(X)|dX<∞.C 大号1-浓度:对于每一个d>0,
$$
\lim {N \rightarrow \infty} \int {|x| \geq \delta}\left|k_{N}X\对| dx=0。
$$
财产一种这个定义说每个函数到ñ在积分为 1 和属性的意义上,具有相同的总“有符号质量”C说这个质量的大部分被挤压成围绕原点越来越小的间隔,因为ñ增加。财产b需要“绝对质量”到ñ独立于ñ. 如果到ñ≥0对于每个ñ, 然后属性一种暗示|到ñ|1=1对于每个ñ, 所以性质b在这种情况下自动满足。
下一个练习描述了构造近似恒等式的“简单”方法:只需选择任何可积函数到其积分为 1 ,然后膨胀到适当地创造到ñ.
数学代写|实分析代写REAL ANALYSIS代考|THE FEJ´ER KERNEL
Fejér 函数是
在(X)=(没有圆周率X圆周率X)2
Fejér 内核是\left{w_{N}\right}_{N \in \mathbb{N}}\left{w_{N}\right}_{N \in \mathbb{N}}在哪里在ñ(X)=ñ在(ñX). 证明在是可积的并且∫在=1. 得出 Fejér 核是一个近似恒等式的结论。
信”在”代表“Weiss”,这是 Fejér 出生时的姓氏。的情节在和在3出现在图中9.3. 我们可以在该图中看到在ñ变得更像尖峰一样ñ增加,就像χ吨变得更像尖峰一样吨→0.
现在我们证明我们的主张,如果\left{k_{N}\right}_{N \in \mathbb{N}}\left{k_{N}\right}_{N \in \mathbb{N}}是一个近似恒等式,那么F∗到ñ→F在大号1-规范每个功能F∈大号1(R). 这个定理的证明说明了两个“标准技巧”。首先,我们介绍到ñ通过使用以下事实进入计算的一项∫到ñ=1. 其次,为了利用大号1-近似恒等式的浓度属性。

数学代写|实分析代写real analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
离散数学代写
Partial Differential Equations代写可以参考一份偏微分方程midterm答案解析