如果你也在 怎样代写凸分析Convex Analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。凸分析Convex Analysis是数学的一个分支,专门研究凸函数和凸集的属性,通常应用于凸最小化,这是优化理论的一个子领域。
my-assignmentexpert™ 凸分析Convex Analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的凸分析Convex Analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此凸分析Convex Analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的凸分析Convex Analysis作业代写代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种凸分析Convex Analysis相关的作业也就用不着 说。
我们提供的凸分析Convex Analysis及其相关学科的代写,服务范围广, 其中包括但不限于:、
- 优化理论 optimization theory
- 变分法 Calculus of variations
- 最优控制理论 Optimal control
- 动态规划 Dynamic programming
- 鲁棒优化 Robust optimization
- 随机优化 Stochastic programming
- 组合优化 Combinatorial optimization
数学代考|凸分析作业代写Convex Analysis代考|Optimality Conditions
Early in multivariate calculus we learn the significance of differentiability in finding minimizers. In this section we begin our study of the interplay between convexity and differentiability in optimality conditions.
For an initial example, consider the problem of minimizing a function $f: C \rightarrow \mathbf{R}$ on a set $C$ in $\mathbf{E}$. We say a point $\bar{x}$ in $C$ is a local minimizer of $f$ on $C$ if $f(x) \geq f(\bar{x})$ for all points $x$ in $C$ close to $\bar{x}$. The directional derivative of a function $f$ at $\bar{x}$ in a direction $d \in \mathbf{E}$ is
$$
f^{\prime}(\bar{x} ; d)=\lim _{t \downarrow 0} \frac{f(\bar{x}+t d)-f(\bar{x})}{t}
$$
when this limit exists. When the directional derivative $f^{\prime}(\bar{x} ; d)$ is actually linear in $d$ (that is, $f^{\prime}(\bar{x} ; d)=\langle a, d\rangle$ for some element $a$ of $\mathbf{E}$ ) then we say $f$ is (Gâteaux) differentiable at $\bar{x}$, with (Gateaux) derivative $\nabla f(\bar{x})=a$. If $f$ is differentiable at every point in $C$ then we simply say $f$ is differentiable (on $C$ ). An example we use quite extensively is the function $X \in \mathbf{S}_{++}^{n} \mapsto$ $\log \operatorname{det} X$. An exercise shows this function is differentiable on $\mathbf{S}_{++}^{n}$ with derivative $X^{-1}$.
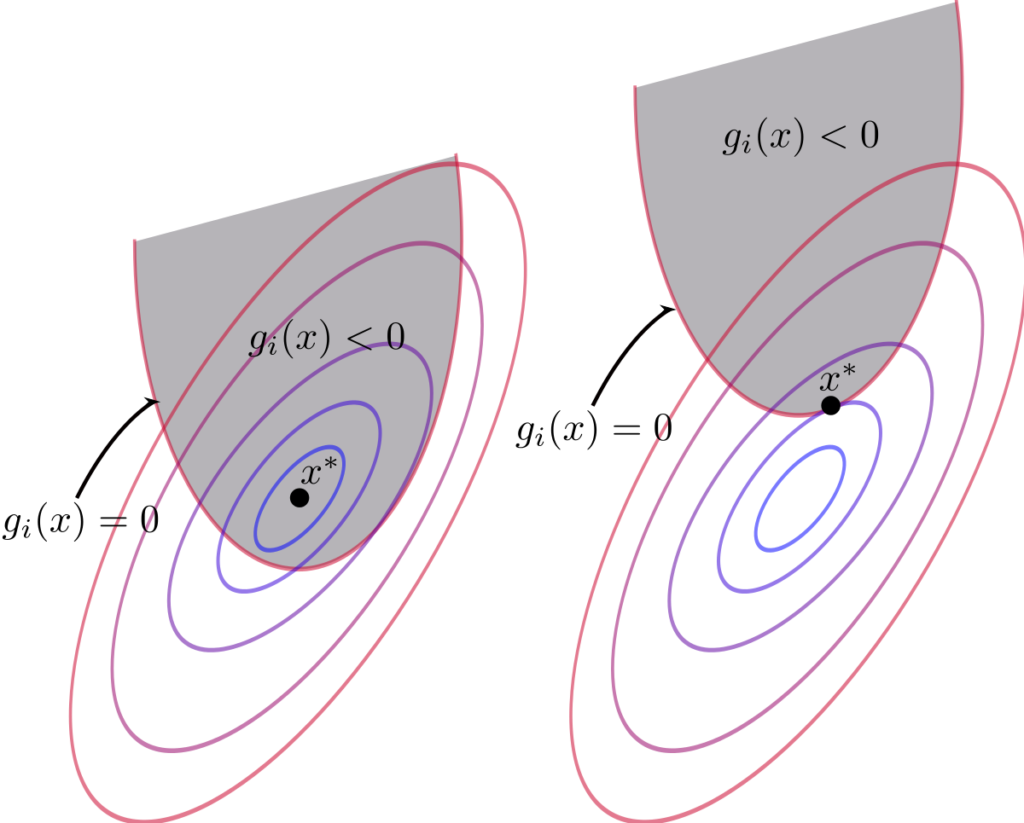
A convex cone which arises frequently in optimization is the normal cone to a convex set $C$ at a point $\bar{x} \in C$, written $N_{C}(\bar{x})$. This is the convex cone of normal vectors, vectors $d$ in $\mathbf{E}$ such that $\langle d, x-\bar{x}\rangle \leq 0$ for all points $x$ in $C$.
数学代考|凸分析作业代写Convex Analysis代考|Theorems of the Alternative
One well-trodden route to the study of first order conditions uses a class of results called “theorems of the alternative”, and, in particular, the Farkas lemma (which we derive at the end of this section). Our first approach, however, relies on a different theorem of the alternative.
Theorem 2.2.1 (Gordan) For any elements $a^{0}, a^{1}, \ldots, a^{m}$ of $\mathbf{E}$, exactly one of the following systems has a solution:
$$
\begin{aligned}
&\sum_{i=0}^{m} \lambda_{i} a^{i}=0, \quad \sum_{i=0}^{m} \lambda_{i}=1, \quad 0 \leq \lambda_{0}, \lambda_{1}, \ldots, \lambda_{m} \in \mathbf{R} \\
&\left\langle a^{i}, x\right\rangle<0 \text { for } i=0,1, \ldots, m, \quad x \in \mathbf{E}
\end{aligned}
$$
Geometrically, Gordan’s theorem says that the origin does not lie in the convex hull of the set $\left\{a^{0}, a^{1}, \ldots, a^{m}\right\}$ if and only if there is an open halfspace $\{y \mid\langle y, x\rangle<0\}$ containing $\left\{a^{0}, a^{1}, \ldots, a^{m}\right\}$ (and hence its convex hull). This is another illustration of the idea of separation (in this case we separate the origin and the convex hull).
Theorems of the alternative like Gordan’s theorem may be proved in a variety of ways, including separation and algorithmic approaches. We employ a less standard technique using our earlier analytic ideas and leading to a rather unified treatment. It relies on the relationship between the optimization problem
$$
\inf \{f(x) \mid x \in \mathbf{E}\}
$$
where the function $f$ is defined by
$$
f(x)=\log \left(\sum_{i=0}^{m} \exp \left\langle a^{i}, x\right\rangle\right)
$$
and the two systems $(2.2 .2)$ and (2.2.3). We return to the surprising function (2.2.5) when we discuss conjugacy in Section $3.3$.
数学代考|凸分析作业代写Convex Analysis代考|Max-functions
This section is an elementary cxposition of the first order necessary conditions for a local minimizer of a differentiable function subject to differentiable inequality constraints. Throughout this section we use the term “differentiable” in the Gâteaux sense, defined in Section 2.1. Our approach, which relies on considering the local minimizers of a max-function
$$
g(x)=\max _{i=0,1, \ldots, m}\left\{g_{i}(x)\right\},
$$
illustrates a pervasive analytic idea in optimization: nonsmoothness. Even if the functions $g_{0}, g_{1}, \ldots, g_{m}$ are smooth, $g$ may not be, and hence the gradient may no longer be a useful notion.
Proposition 2.3.2 (Directional derivatives of max-functions) Let $\bar{x}$ be a point in the interior of a set $C \subset \mathbf{E}$. Suppose that continuous functions $g_{0}, g_{1}, \ldots, g_{m}: C \rightarrow \mathbf{R}$ are differentiable at $\bar{x}$, that $g$ is the max-function (2.3.1), and define the index set $K=\left\{i \mid g_{i}(\bar{x})=g(\bar{x})\right\}$. Then for all directions $d$ in $\mathbf{E}$, the directional derivative of $g$ is given by
$$
g^{\prime}(\bar{x} ; d)=\max _{i \in K}\left\{\left\langle\nabla g_{i}(\bar{x}), d\right\rangle\right\}
$$

数学代考|凸分析作业代写CONVEX ANALYSIS代考|OPTIMALITY CONDITIONS
在多元微积分的早期,我们学习了可微性在寻找极小值中的重要性。在本节中,我们开始研究最优性条件下凸性和可微性之间的相互作用。
对于初始示例,考虑最小化函数的问题F:C→R在一组C在和. 我们说一点X¯在C是一个局部最小化器F在C如果F(X)≥F(X¯)对于所有点X在C相近X¯. 函数的方向导数F在X¯在一个方向d∈和是
$$
f^{\prime}(\bar{x} ; d)=\lim {t \downarrow 0} \frac{f(\bar{x}+t d)-f(\bar{x})}{t} $$ when this limit exists. When the directional derivative $f^{\prime}(\bar{x} ; d)$ is actually linear in $d$ (that is, $f^{\prime}(\bar{x} ; d)=\langle a, d\rangle$ for some element $a$ of $\mathbf{E}$ ) then we say $f$ is (Gâteaux) differentiable at $\bar{x}$, with (Gateaux) derivative $\nabla f(\bar{x})=a$. If $f$ is differentiable at every point in $C$ then we simply say $f$ is differentiable (on $C$ ). An example we use quite extensively is the function $X \in \mathbf{S}{++}^{n} \mapsto$ $\log \operatorname{det} X$. An exercise shows this function is differentiable on $\mathbf{S}_{++}^{n}$ with derivative $X^{-1}$.
优化中经常出现的凸锥是凸集的法向锥C在某一点X¯∈C, 写ñC(X¯). 这是法向量的凸锥,向量d在和这样⟨d,X−X¯⟩≤0对于所有点X在C.
数学代考|凸分析作业代写CONVEX ANALYSIS代考|THEOREMS OF THE ALTERNATIVE
研究一阶条件的一条行之有效的方法是使用称为“替代定理”的一类结果,特别是法卡斯引理在H一世CH在和d和r一世v和一种吨吨H和和nd这F吨H一世ss和C吨一世这n. 然而,我们的第一种方法依赖于另一种选择的不同定理。
定理 2.2.1G这rd一种n对于任何元素一种0,
$$
\begin{aligned}
&\sum_{i=0}^{m} \lambda_{i} a^{i}=0, \quad \sum_{i=0}^{m} \lambda_{i}=1, \quad 0 \leq \lambda_{0}, \lambda_{1}, \ldots, \lambda_{m} \in \mathbf{R} \
&\left\langle a^{i}, x\right\rangle<0 \text { for } i=0,1, \ldots, m, \quad x \in \mathbf{E}
\end{aligned}
$$
像 Gordan 定理这样的替代定理可以通过多种方式来证明,包括分离和算法方法。我们使用我们早期的分析思想采用了一种不太标准的技术,并导致了相当统一的处理。它依赖于优化问题之间的关系
信息{F(X)∣X∈和}
函数在哪里F定义为
F(X)=日志(∑一世=0米经验⟨一种一世,X⟩)
和两个系统(2.2.2)和2.2.3. 我们回到令人惊讶的功能2.2.5当我们在章节中讨论共轭时3.3.
数学代考|凸分析作业代写CONVEX ANALYSIS代考|MAX-FUNCTIONS
本节是受可微不等式约束的可微函数的局部极小化的一阶必要条件的基本解释。在本节中,我们使用第 2.1 节中定义的 Gâteaux 意义上的术语“可微分”。我们的方法,它依赖于考虑最大函数的局部最小值
G(X)=最大限度一世=0,1,…,米{G一世(X)},
说明了优化中普遍存在的分析思想:非平滑性。即使函数G0,G1,…,G米光滑,G可能不是,因此梯度可能不再是一个有用的概念。
命题 2.3.2D一世r和C吨一世这n一种一世d和r一世v一种吨一世v和s这F米一种X−F你nC吨一世这ns让X¯成为集合内部的一个点C⊂和. 假设连续函数G0,G1,…,G米:C→R可微分于X¯, 那G是最大函数2.3.1,并定义索引集到={一世∣G一世(X¯)=G(X¯)}. 然后对于所有方向d在和, 的方向导数G是(谁)给的
G′(X¯;d)=最大限度一世∈到{⟨∇G一世(X¯),d⟩}

数学代考|凸分析作业代写Convex Analysis代考 请认准UpriviateTA. UpriviateTA为您的留学生涯保驾护航。
更多内容请参阅另外一份复分析代写.