
I have the following basic linear optimization problem. Let $A \in \mathbb{R}^{n, n}, c \in \mathbb{R}^{n}$, then solve
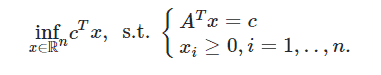
According to my lecture notes, the dual problem is this:
$$
\sup _{y \in \mathbb{R}^{n}} c^{T} y, \quad, \text { s.t. } A y \leq b
$$
Now, when I try to derive this formula by myself, I get something different. First I set
$$
L(x, u, v)=c^{T} x+u^{T}\left(A^{T} x-c\right)+v^{T} x=\left(c^{T}+u^{T} A^{T}+v^{T}\right) x-u^{T} c
$$
Then minimizing w.r.t. $x$ needs that
$$
0 \stackrel{!}{=} \frac{\partial L}{\partial x}(x, u, v)=\left(c^{T}+u^{T} A+v^{T}\right)
$$
The dual function is then
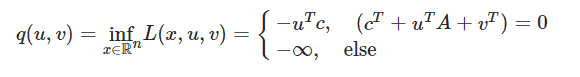
Then I get the dual problem as
$$
\sup _{u, v}-u^{T} c, \text { s.t. }(c+A u+v)=0
$$
There s a sign constraint for $v \leq 0$ so that the Lagrangian is a lower bound of the original objective function.
Let $-u=y$, then we have $\sup _{u, v} y^{T} c$ in our dual with the constraint:
$$
c+A u+v=0
$$
Since $v \leq 0$, it can be written as $c+A u \geq 0$.
$$
\begin{aligned}
A u \geq-c \
-A y & \geq-c \
A y \leq c
\end{aligned}
$$
Consider a non-oriented graph $G=(N, E)$, with $n=|N|$ and weight $c_{i, j}$ associated to the edges
$(i, j)$ in $E$.
- Consider a vertex $a$ in $N$. Write the ILP model to find two spanning trees of minimum total length, without common edges and such that one of them has the number of edges incident to $a$ exactly equal to 3 .
- Consider now a set of vertices $S$ in $N$. Write the ILP model to find two spanning trees of minimum total length, without common edges and such that they touch the vertices of $S$ in a balanced way: incident edges to every vertex $a$ in $S$ used by one of the two trees cannot be greater than two times of edges used by other tree.
attempt for the question 1.:let $x_{i, j}=1$ if I choose the edge $(i, j)$ for the tree $T_{1}$ and $o$ otherwise. The same for the other tree $T_{2}$ with the labels $y_{i, j}$. This is my ILP model:
$$
\begin{aligned}
\operatorname{minimize} \sum_{(i, j) \in E} c_{i, j}\left(x_{i, j}+y_{i, j}\right) & \
\sum_{(i, j) \in E} x_{i, j} &=n-1 \
\sum_{(i, j) \in E} y_{i, j} &=n-1 \
\sum_{(i, j) \in E(S)} x_{i, j} & \leq|S|-1 \quad \text { for every } S \subseteq N \
\sum_{(i, j) \in E(S)} y_{i, j} & \leq|S|-1 \quad \text { for every } S \subseteq N \
x_{i, j}+y_{i, j} & \leq 1 \quad \
\sum_{(i, j) \in \delta(a)} x_{i, j} &=3
\end{aligned}
$$
where $E(S)={(i, j) \in E \mid i \in S, j \in S} ; \delta(a)={(i, j) \in E \mid i=a$ or $j=a}$. The first four conditions are the classic conditions for minimum spanning trees to be connected and without cycles. The fifth condition is the fact that the trees have no common edges.

数学代考,运筹学代写Operations Research请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
Fourier analysis代写
微分几何代写
离散数学代写
Partial Differential Equations代写可以参考一份偏微分方程midterm答案解析
Pingback: 数学代写|时间序列分析代写time 代写 | UprivateTA™- 数学代写