如果你也在 怎样代写计量经济学Econometrics是将统计方法应用于经济数据,以赋予经济关系以经验内容。更确切地说,它是 “基于理论和观察的同步发展,通过适当的推理方法对实际经济现象进行定量分析”。 一本经济学入门教科书将计量经济学描述为允许经济学家 “从堆积如山的数据中筛选出简单的关系”。
计量经济学Econometrics的一个基本工具是多元线性回归模型。计量经济学理论使用统计理论和数理统计来评估和发展计量经济学方法。计量经济学家试图找到具有理想统计特性的估计器,包括无偏性、效率和一致性。应用计量经济学使用理论计量经济学和现实世界的数据来评估经济理论,开发计量经济学模型,分析经济历史和预测。
my-assignmentexpert™ 计量经济学Econometrics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的计量经济学Econometrics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计量经济学Econometrics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计量经济学Econometrics代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种计量经济学Econometrics相关的作业也就用不着 说。
我们提供的计量经济学Econometrics及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|计量经济学代写Econometrics代考|Lebesgue Measure
Along similar lines as in the construction of the uniform probability measure we can define the Lebesgue measure as follows. Consider a function $\lambda$ that assigns its length to each open interval $(a, b), \lambda((a, b))=b-a$, and define for all other Borel sets $B$ in $\mathbb{R}$,
$$
\lambda(B)=\inf {B \subset \cup{j=1}^{\infty}\left(a_{j}, b_{j}\right)} \sum_{j=1}^{\infty} \lambda\left(\left(a_{j}, b_{j}\right)\right)=\inf {B \subset \cup{j=1}^{\infty}\left(a_{j}, b_{j}\right)} \sum_{j=1}^{\infty}\left(b_{j}-a_{j}\right) .
$$
This function $\lambda$ is called the Lebesgue measure on $\mathbb{R}$, which measures the total “length” of a Borel set, where the measurement is taken from the outside.
Similarly, now let $\lambda\left(\times_{i=1}^{k}\left(a_{i}, b_{i}\right)\right)=\prod_{i=1}^{k}\left(b_{i}-a_{i}\right)$ and define
$$
\begin{aligned}
\lambda(B) &=\inf {\left.B \subset \cup{j=1}^{\infty} \mid x_{i=1}^{k}\left(a_{i, j}, b_{i, j}\right)\right}} \sum_{j=1}^{\infty} \lambda\left(\times_{i=1}^{k}\left(a_{i, j}, b_{i, j}\right)\right) \
&=\inf {B \subset \cup{j=1}^{\infty}\left{\left(x_{i=1}^{k}\left(a_{i, j}, b_{i, j}\right)\right}\right.} \sum_{j=1}^{\infty}\left{\prod_{i=1}^{k}\left(b_{i, j}-a_{i, j}\right)\right},
\end{aligned}
$$
for all other Borel sets $B$ in $\mathbb{R}^{k}$. This is the Lebesgue measure on $\mathbb{R}^{k}$, which measures the area (in the case $k=2$ ) or the volume (in the case $k \geq 3$ ) of a Borel set in $\mathbb{R}^{k}$, where again the measurement is taken from the outside.
Note that, in general, Lebesgue measures are not probability measures because the Lebesgue measure can be infinite. In particular, $\lambda\left(\mathbb{R}^{k}\right)=\infty$. However, if confined to a set with Lebesgue measure 1, this measure becomes the uniform probability measure. More generally, for any Borel set $A \in \mathbb{R}^{k}$ with positive and finite Lebesgue measure, $\mu(B)=\lambda(A \cap B) / \lambda(A)$ is the uniform probability measure on $\boldsymbol{3}^{k} \cap A$.
经济代写|计量经济学代写Econometrics代考|Lebesgue Integral
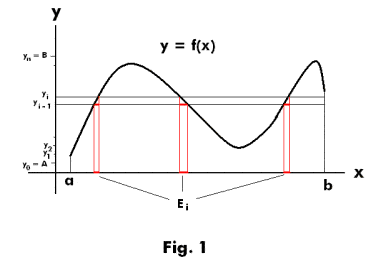
The Lebesgue measure gives rise to a generalization of the Riemann integral. Recall that the Riemann integral of a nonnegative function $f(x)$ over a finite interval $(a, b]$ is defined as
$$
\int_{a}^{b} f(x) d x=\sup \sum_{m=1}^{n}\left(\inf {x \in I{m}} f(x)\right) \lambda\left(I_{m}\right),
$$
where the $I_{m}$ ‘s are intervals forming a finite partition of $(a, b]-$ that is, they are disjoint and their union is $(a, b]:(a, b]=\cup_{m=1}^{n} I_{m}-$ and $\lambda\left(I_{m}\right)$ is the length of $I_{m}$; hence, $\lambda\left(I_{m}\right)$ is the Lebesgue measure of $I_{m}$, and the supremum is taken over all finite partitions of $(a, b]$. Mimicking the definition of Riemann integral, the Lebesgue integral of a nonnegative function $f(x)$ over a Borel set $A$ can be defined as
$$
\int_{A} f(x) d x=\sup \sum_{m=1}^{n}\left(\inf {x \in B{m}} f(x)\right) \lambda\left(B_{m}\right)
$$
where now the $B_{m}$ ‘s are Borel sets forming a finite partition of $A$ and the supremum is taken over all such partitions.
If the function $f(x)$ is not nonnegative, we can always write it as the difference of two nonnegative functions: $f(x)=f_{+}(x)-f_{-}(x)$, where
$$
f_{+}(x)=\max [0, f(x)], \quad f_{-}(x)=\max [0,-f(x)]
$$
Then the Lebesgue integral over a Borel set $A$ is defined as
$$
\int_{A} f(x) d x=\int_{A} f_{+}(x) d x-\int_{A} f_{-}(x) d x
$$
provided that at least one of the right-hand integrals is finite.
However, we still need to impose a further condition on the function $f$ in order for it to be Lebesgue integrable. A sufficient condition is that, for each Borel set $B$ in $\mathbb{R}$, the set ${x: f(x) \in B}$ is a Borel set itself. As we will see in the next chapter, this is the condition for Borel measurability of $f$.
Finally, note that if $A$ is an interval and $f(x)$ is Riemann integrable over $A$, then the Riemann and the Lebesgue integrals coincide.
计量经济学代写
经济代写|计量经济学代写ECONOMETRICS代考|LEBESGUE MEASURE
沿着与构建统一概率测度类似的思路,我们可以将 Lebesgue 测度定义如下。考虑一个函数λ将其长度分配给每个开区间(一种,b),λ((一种,b))=b−一种, 并为所有其他 Borel 集定义乙在R,
$$
\lambda(B)=\inf {B \subset \cup{j=1}^{\infty}\left(a_{j}, b_{j}\right)} \sum_{j=1}^{\infty} \lambda\left(\left(a_{j}, b_{j}\right)\right)=\inf {B \subset \cup{j=1}^{\infty}\left(a_{j}, b_{j}\right)} \sum_{j=1}^{\infty}\left(b_{j}-a_{j}\right) .
$$
This function $\lambda$ is called the Lebesgue measure on $\mathbb{R}$, which measures the total “length” of a Borel set, where the measurement is taken from the outside.
Similarly, now let $\lambda\left(\times_{i=1}^{k}\left(a_{i}, b_{i}\right)\right)=\prod_{i=1}^{k}\left(b_{i}-a_{i}\right)$ and define
$$
\begin{aligned}
\lambda(B) &=\inf {\left.B \subset \cup{j=1}^{\infty} \mid x_{i=1}^{k}\left(a_{i, j}, b_{i, j}\right)\right}} \sum_{j=1}^{\infty} \lambda\left(\times_{i=1}^{k}\left(a_{i, j}, b_{i, j}\right)\right) \
&=\inf {B \subset \cup{j=1}^{\infty}\left{\left(x_{i=1}^{k}\left(a_{i, j}, b_{i, j}\right)\right}\right.} \sum_{j=1}^{\infty}\left{\prod_{i=1}^{k}\left(b_{i, j}-a_{i, j}\right)\right},
\end{aligned}
$$
对于所有其他 Borel 集乙在Rķ. 这是勒贝格测度Rķ, 测量面积一世n吨H和C一种s和$ķ=2$或音量一世n吨H和C一种s和$ķ≥3$一个Borel设置在Rķ,再次从外部进行测量。
请注意,一般来说,勒贝格测度不是概率测度,因为勒贝格测度可以是无限的。尤其,λ(Rķ)=∞. 但是,如果限制在具有 Lebesgue 测度 1 的集合中,该测度将成为统一概率测度。更一般地,对于任何 Borel 集一种∈Rķ具有正的和有限的勒贝格测度,μ(乙)=λ(一种∩乙)/λ(一种)是一致的概率测度3ķ∩一种.
经济代写|计量经济学代写ECONOMETRICS代考|LEBESGUE INTEGRAL
勒贝格测度引起了黎曼积分的推广。回想一下非负函数的黎曼积分F(X)在有限的区间内(一种,b]定义为
$$
\int_{a}^{b} fXdx=\sup \sum_{m=1}^{n}\left(\inf {x \in I {m}} fX\right) \lambda\left我是正确的我是正确的,
$$
在哪里一世米是形成有限分区的区间(一种,b]−也就是说,它们是不相交的,它们的联合是(一种,b]:(一种,b]=∪米=1n一世米−和λ(一世米)是长度一世米; 因此,λ(一世米)是勒贝格测度一世米, 并且上确界被接管 的所有有限分区(一种,b]. 模仿黎曼积分的定义,非负函数的勒贝格积分F(X)在 Borel 集上一种可以定义为
$$
\int_{A} fXdx=\sup \sum_{m=1}^{n}\left(\inf {x \in B {m}} fX\right) \lambda\leftB_{m}\右B_{m}\右
$$
现在在哪里乙米是 Borel 集形成的有限分区一种并且上界被接管所有这样的分区。
如果函数F(X)不是非负的,我们总是可以把它写成两个非负函数的差:F(X)=F+(X)−F−(X), 在哪里
F+(X)=最大限度[0,F(X)],F−(X)=最大限度[0,−F(X)]
然后是 Borel 集上的 Lebesgue 积分一种定义为
∫一种F(X)dX=∫一种F+(X)dX−∫一种F−(X)dX
前提是至少有一个右手积分是有限的。
但是,我们仍然需要对函数施加进一步的条件F使其成为 Lebesgue 可积的。一个充分条件是,对于每个 Borel 集乙在R, 集合X:F(X)∈乙本身就是一个 Borel 集。正如我们将在下一章中看到的,这是 Borel 可测性的条件F.
最后,请注意,如果一种是一个区间并且F(X)是黎曼可积的一种,则黎曼积分和勒贝格积分重合。

经济代写|计量经济学代写Econometrics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。