如果你也在 怎样代写计量经济学Econometrics是将统计方法应用于经济数据,以赋予经济关系以经验内容。更确切地说,它是 “基于理论和观察的同步发展,通过适当的推理方法对实际经济现象进行定量分析”。 一本经济学入门教科书将计量经济学描述为允许经济学家 “从堆积如山的数据中筛选出简单的关系”。
计量经济学Econometrics的一个基本工具是多元线性回归模型。计量经济学理论使用统计理论和数理统计来评估和发展计量经济学方法。计量经济学家试图找到具有理想统计特性的估计器,包括无偏性、效率和一致性。应用计量经济学使用理论计量经济学和现实世界的数据来评估经济理论,开发计量经济学模型,分析经济历史和预测。
my-assignmentexpert™ 计量经济学Econometrics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的计量经济学Econometrics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计量经济学Econometrics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计量经济学Econometrics代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种计量经济学Econometrics相关的作业也就用不着 说。
我们提供的计量经济学Econometrics及其相关学科的代写,服务范围广, 其中包括但不限于:

经济代写|计量经济学代写Econometrics代考|Random Variables and Vectors
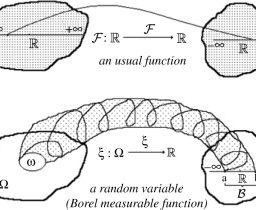
In broad terms, a random variable is a numerical translation of the outcomes of a statistical experiment. For example, flip a fair coin once. Then the sample space is $\Omega={\mathrm{H}, \mathrm{T}}$, where $\mathrm{H}$ stands for heads and T stands for tails. The $\sigma$-algebra involved is $\mathscr{F}={\Omega, \emptyset,{\mathrm{H}},{\mathrm{T}}}$, and the corresponding probability measure is defined by $P({\mathrm{H}})=P({\mathrm{~T}}})=1 / 2$. Now define the function $X(\omega)=1$ if $\omega=\mathrm{H}, X(\omega)=0$ if $\omega=\mathrm{T}$. Then $X$ is a random variable that takes the value 1 with probability $1 / 2$ and the value 0 with probability $1 / 2$ :
$$
\begin{aligned}
&P(X=1) \stackrel{\text { (shorthand notation) }}{=} P({\omega \in \Omega: X(\omega)=1})=P({\mathrm{H}})=1 / 2, \
&P(X=0) \stackrel{\text { (shorthand notation) }}{=} P({\omega \in \Omega: X(\omega)=0})=P({\mathrm{~T}})=1 / 2 .
\end{aligned}
$$
Moreover, for an arbitrary Borel set $B$ we have $P(X \in B)=$
where, again, $P(X \in B)$ is a shorthand notation ${ }^{9}$ for $P({\omega \in \Omega: X(\omega) \in B})$.
In this particular case, the set ${\omega \in \Omega: X(\omega) \in B}$ is automatically equal to one of the elements of $\mathscr{F}$, and therefore the probability $P(X \in B)=$ $P({\omega \in \Omega: X(\omega) \in B})$ is well-defined. In general, however, we need to confine the mappings $X: \Omega \rightarrow \mathbb{R}$ to those for which we can make probability statements about events of the type ${\omega \in \Omega: X(\omega) \in B}$, where $B$ is an arbitrary Borel set, which is only possible if these sets are members of $\mathscr{F}$ :
经济代写|计量经济学代写Econometrics代考|Distribution Functions
For Borel sets of the type $(-\infty, x]$, or $\times_{j=1}^{k}\left(-\infty, x_{j}\right]$ in the multivariate case, the value of the induced probability measure $\mu_{X}$ is called the distribution function:
Definition 1.11: Let $X$ be a random variable $(k=1)$ or a random vector $(k>1)$ with induced probability measure $\mu_{X}$. The function $F(x)=$ $\mu_{X}\left(\times_{j=1}^{k}\left(-\infty, x_{j}\right]\right), x=\left(x_{1}, \ldots, x_{k}\right)^{\mathrm{T}} \in \mathbb{R}^{k}$ is called the distribution function of $X$.
It follows from these definitions and Theorem $1.8$ that
Theorem 1.11: A distribution function of a random variable is always right continuous, that is, $\forall x \in \mathbb{R}, \lim {\delta \downarrow 0} F(x+\delta)=F(x)$, and monotonic nondecreasing, that is, $F\left(x{1}\right) \leq F\left(x_{2}\right)$ if $x_{1}{x \downarrow-\infty} F(x)=0$, $\lim {x \uparrow \infty} F(x)=1$. Proof: Exercise. However, a distribution function is not always left continuous. As a counterexample, consider the distribution function of the binomial $(n, p)$ distribution in Section 1.2.2. Recall that the corresponding probability space consists of sample space $\Omega={0,1,2, \ldots, n}$, the $\sigma$-algebra $\mathscr{F}$ of all subsets of $\Omega$, and probability measure $P({k})$ defined by (1.15). The random variable $X$ involved is defined as $X(k)=k$ with distribution function $F(x)=0 \quad$ for $\quad x<0$, $F(x)=\sum_{k \leq x} P({k})$ for $x \in[0, n]$, $F(x)=1 \quad$ for $x>n .$
Now, for example, let $x=1$. Then, for $0<\delta<1, F(1-\delta)=F(0)$, and $F(1+\delta)=F(1)$; hence, $\lim {\delta \downarrow 0} F(1+\delta)=F(1)$, but $\lim {\delta \downarrow 0} F(1-\delta)=$ $F(0)<F(1)$.
计量经济学代写
经济代写|计量经济学代写ECONOMETRICS代考|RANDOM VARIABLES AND VECTORS
从广义上讲,随机变量是统计实验结果的数值转换。例如,抛一次公平的硬币。那么样本空间是Ω=H,吨, 在哪里H代表正面,T 代表反面。这σ- 涉及的代数是F=Ω,∅,H,吨, 对应的概率测度定义为P ({\ mathrm {H}}) = P (\ mathrm ~ T}}}) = 1/2P ({\ mathrm {H}}) = P (\ mathrm ~ T}}}) = 1/2. 现在定义函数X(ω)=1如果ω=H,X(ω)=0如果ω=吨. 然后X是一个随机变量,它以概率取值 11/2和概率值为 01/2:
磷(X=1)= (简写符号) 磷(ω∈Ω:X(ω)=1)=磷(H)=1/2, 磷(X=0)= (简写符号) 磷(ω∈Ω:X(ω)=0)=磷( 吨)=1/2.
此外,对于任意 Borel 集乙我们有磷(X∈乙)=
在哪里,再次,磷(X∈乙)是一种速记符号9为了磷(ω∈Ω:X(ω)∈乙).
在这种特殊情况下,集合ω∈Ω:X(ω)∈乙自动等于的元素之一F,因此概率磷(X∈乙)= 磷(ω∈Ω:X(ω)∈乙)是明确的。然而,一般来说,我们需要限制映射X:Ω→R对于那些我们可以对此类事件做出概率陈述的人ω∈Ω:X(ω)∈乙, 在哪里乙是一个任意的 Borel 集,只有当这些集合是F:
经济代写|计量经济学代写ECONOMETRICS代考|DISTRIBUTION FUNCTIONS
对于类型的 Borel 集(−∞,X], 或者×j=1ķ(−∞,Xj]在多变量情况下,诱导概率测度的值μX称为分布函数:
定义 1.11:让X是一个随机变量(ķ=1)或随机向量(ķ>1)用诱导概率测度μX. 功能F(X)= μX(×j=1ķ(−∞,Xj]),X=(X1,…,Xķ)吨∈Rķ称为分布函数X.
它遵循这些定义和定理1.8即
定理 1.11:随机变量的分布函数总是右连续的,即$\forall x \in \mathbb{R}, \lim {\delta \downarrow 0} F(x+\delta)=F(x)$, and monotonic nondecreasing, that is, $F\left(x{1}\right) \leq F\left(x_{2}\right)$ if $x_{1}{x \downarrow-\infty} F(x)=0$, $\lim {x \uparrow \infty} F(x)=1$. Proof: Exercise. However, a distribution function is not always left continuous. As a counterexample, consider the distribution function of the binomial $(n, p)$ distribution in Section 1.2.2. Recall that the corresponding probability space consists of sample space $\Omega={0,1,2, \ldots, n}$, the $\sigma$-algebra $\mathscr{F}$ of all subsets of $\Omega$, and probability measure $P({k})$ defined by (1.15). The random variable $X$ involved is defined as $X(k)=k$ with distribution function $F(x)=0 \quad$ for $\quad x<0$, $F(x)=\sum_{k \leq x} P({k})$ for $x \in[0, n]$, $F(x)=1 \quad$ for $x>n .$
Now, for example, let $x=1$. Then, for $0<\delta<1, F(1-\delta)=F(0)$, and $F(1+\delta)=F(1)$; hence, $\lim {\delta \downarrow 0} F(1+\delta)=F(1)$, but $\lim {\delta \downarrow 0} F(1-\delta)=$ $F(0)<F(1)$.

经济代写|计量经济学代写Econometrics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。