如果你也在 怎样代写计量经济学Econometrics是将统计方法应用于经济数据,以赋予经济关系以经验内容。更确切地说,它是 “基于理论和观察的同步发展,通过适当的推理方法对实际经济现象进行定量分析”。 一本经济学入门教科书将计量经济学描述为允许经济学家 “从堆积如山的数据中筛选出简单的关系”。
计量经济学Econometrics的一个基本工具是多元线性回归模型。计量经济学理论使用统计理论和数理统计来评估和发展计量经济学方法。计量经济学家试图找到具有理想统计特性的估计器,包括无偏性、效率和一致性。应用计量经济学使用理论计量经济学和现实世界的数据来评估经济理论,开发计量经济学模型,分析经济历史和预测。
my-assignmentexpert™ 计量经济学Econometrics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的计量经济学Econometrics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计量经济学Econometrics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计量经济学Econometrics代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种计量经济学Econometrics相关的作业也就用不着 说。
我们提供的计量经济学Econometrics及其相关学科的代写,服务范围广, 其中包括但不限于:
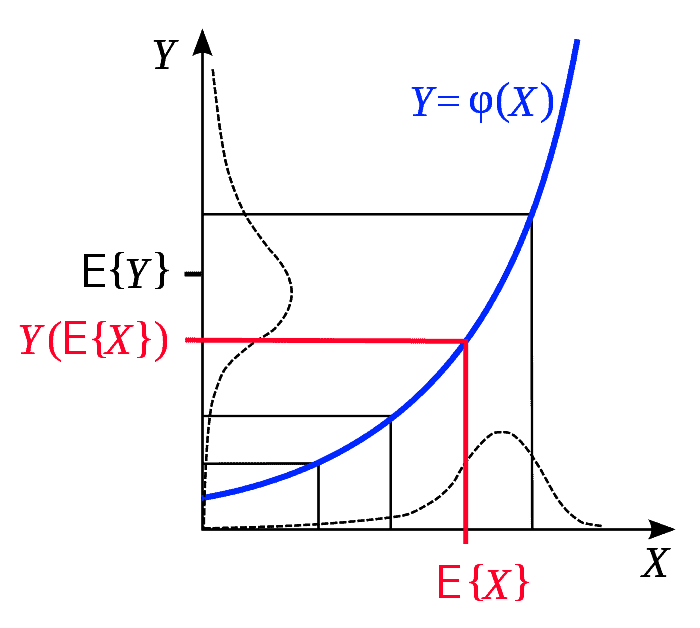
经济代写|计量经济学代写Econometrics代考|Chebishev’s Inequality
Let $X$ be a nonnegative random variable with distribution Function $F(x)$, and let $\varphi(x)$ be a monotonic, increasing, nonnegative Borel-measurable function on $[0, \infty)$. Then, for arbitrary $\varepsilon>0$,
$$
\begin{aligned}
E[\varphi(X)]=& \int \varphi(x) d F(x)=\int_{{\varphi(x)>\varphi(\varepsilon)}} \varphi(x) d F(x) \
&+\int_{{\varphi(x) \leq \varphi(\varepsilon)}} \varphi(x) d F(x) \geq \int_{{\varphi(x)>\varphi(\varepsilon)}} \varphi(x) d F(x) \geq \varphi(\varepsilon) \
& \times \int_{{\varphi(x)>\varphi(\varepsilon)}} d F(x)=\varphi(\varepsilon) \int_{{x>\varepsilon}} d F(x)=\varphi(\varepsilon)(1-F(\varepsilon))
\end{aligned}
$$
hence,
$$
P(X>\varepsilon)=1-F(\varepsilon) \leq E[\varphi(X)] / \varphi(\varepsilon)
$$
In particular, it follows from $(2.19)$ that, for a random variable $Y$ with expected value $\mu_{y}=E(Y)$ and variance $\sigma_{y}^{2}$,
$$
P\left(\left{\omega \in \Omega:\left|Y(\omega)-\mu_{y}\right|>\sqrt{\sigma_{y}^{2} / \varepsilon}\right}\right) \leq \varepsilon
$$
经济代写|计量经济学代写Econometrics代考|Holder’s Inequality
Holder’s inequality is based on the fact that $\ln (x)$ is a concave function on $(0, \infty)$ : for $01$ and $p^{-1}+q^{-1}=1$. Then it follows from (2.21), with $\lambda=1 / p$ and $1-\lambda=1 / q$, that
$$
\begin{aligned}
&p^{-1} \frac{|X|^{p}}{E\left(|X|^{p}\right)}+q^{-1} \frac{|Y|^{q}}{E\left(|Y|^{q}\right)} \geq\left(\frac{|X|^{p}}{E\left(|X|^{p}\right)}\right)^{1 / p}\left(\frac{|Y|^{q}}{E\left(|Y|^{q}\right)}\right)^{1 / q} \
&=\frac{|X \cdot Y|}{\left(E\left(|X|^{p}\right)\right)^{1 / p}\left(E\left(|Y|^{q}\right)\right)^{1 / q}} .
\end{aligned}
$$
Taking expectations yields Holder’s inequality:
$$
E(|X \cdot Y|) \leq\left(E\left(|X|^{p}\right)\right)^{1 / p}\left(E\left(|Y|^{q}\right)\right)^{1 / q},
$$
where $p>1$ and $\frac{1}{p}+\frac{1}{q}=1$.For the case $p=q=2$, inequality (2.22) reads $E(|X \cdot Y|) \leq \sqrt{E\left(X^{2}\right)} \sqrt{E\left(Y^{2}\right)}$, which is known as the Cauchy-Schwartz inequality.
经济代写|计量经济学代写ECONOMETRICS代考|Liapounov’s Inequality
Liapounov’s inequality follows from Holder’s inequality (2.22) by replacing $Y$ with 1:
$$
E(|X|) \leq\left(E\left(|X|^{p}\right)\right)^{1 / p}, \quad \text { where } \quad p \geq 1
$$
经济代写|计量经济学代写ECONOMETRICS代考|Minkowski’s Inequality
If for some $p \geq 1, E\left[|X|^{p}\right]<\infty$ and $E\left[|Y|^{p}\right]<\infty$, then $$ E(|X+Y|) \leq\left(E\left(|X|^{p}\right)\right)^{1 / p}+\left(E\left(|Y|^{p}\right)\right)^{1 / p} . $$ This inequality is due to Minkowski. For $p=1$ the result is trivial. Therefore, let $p>1$. First note that $E\left[|X+Y|^{p}\right] \leq E\left[(2 \cdot \max (|X|,|Y|))^{p}\right]=$ $2^{p} E\left[\max \left(|X|^{p},|Y|^{p}\right)\right] \leq 2^{p} E\left[|X|^{p}+|Y|^{p}\right]<\infty$; hence, we may apply Liapounov’s inequality:
$$
E(|X+Y|) \leq\left(E\left(|X+Y|^{p}\right)\right)^{1 / p} .
$$
Next, observe that
$$
\begin{aligned}
E\left(|X+Y|^{p}\right)=& E\left(|X+Y|^{p-1}|X+Y|\right) \leq E\left(|X+Y|^{p-1}|X|\right) \
&+E\left(|X+Y|^{p-1}|Y|\right) .
\end{aligned}
$$
Let $q=p /(p-1)$. Because $1 / q+1 / p=1$ it follows from Holder’s inequality that
$$
\begin{aligned}
E\left(|X+Y|^{p-1}|X|\right) & \leq\left(E\left(|X+Y|^{(p-1) q}\right)\right)^{1 / q}\left(E\left(|X|^{p}\right)\right)^{1 / p} \
& \leq\left(E\left(|X+Y|^{p}\right)\right)^{1-1 / p}\left(E\left(|X|^{p}\right)\right)^{1 / p}
\end{aligned}
$$
and similarly,
$$
E\left(|X+Y|^{p-1}|Y|\right) \leq\left(E\left(|X+Y|^{p}\right)\right)^{1-1 / p}\left(E\left(|Y|^{p}\right)\right)^{1 / p} .
$$
If we combine (2.24)-(2.26), Minkowski’s inequality (2.23) follows.
计量经济学代写
经济代写|计量经济学代写ECONOMETRICS代考|CHEBISHEV’S INEQUALITY
让X是具有分布函数的非负随机变量F(X), 然后让披(X)是一个单调的、递增的、非负的 Borel 可测函数[0,∞). 那么,对于任意e>0,
和[披(X)]=∫披(X)dF(X)=∫披(X)>披(e)披(X)dF(X) +∫披(X)≤披(e)披(X)dF(X)≥∫披(X)>披(e)披(X)dF(X)≥披(e) ×∫披(X)>披(e)dF(X)=披(e)∫X>edF(X)=披(e)(1−F(e))
因此,
磷(X>e)=1−F(e)≤和[披(X)]/披(e)
特别是,它来自(2.19)那,对于一个随机变量是有期望值μ是=和(是)和方差σ是2,
P\left(\left{\omega \in \Omega:\left|Y(\omega)-\mu_{y}\right|>\sqrt{\sigma_{y}^{2} / \varepsilon}\right }\right) \leq \varepsilonP\left(\left{\omega \in \Omega:\left|Y(\omega)-\mu_{y}\right|>\sqrt{\sigma_{y}^{2} / \varepsilon}\right }\right) \leq \varepsilon
经济代写|计量经济学代写ECONOMETRICS代考|HOLDER’S INEQUALITY
Holder 不等式基于以下事实:ln(X)是一个凹函数(0,∞): 为了01和p−1+q−1=1. 然后它遵循从2.21, 和λ=1/p和1−λ=1/q, 那
p−1|X|p和(|X|p)+q−1|是|q和(|是|q)≥(|X|p和(|X|p))1/p(|是|q和(|是|q))1/q =|X⋅是|(和(|X|p))1/p(和(|是|q))1/q.
取期望产生 Holder 不等式:
和(|X⋅是|)≤(和(|X|p))1/p(和(|是|q))1/q,
在哪里p>1和1p+1q=1.对于案例p=q=2, 不等式2.22读和(|X⋅是|)≤和(X2)和(是2),这被称为柯西-施瓦茨不等式。
经济代写|计量经济学代写ECONOMETRICS代考|LIAPOUNOV’S INEQUALITY
Liapounov 不等式源自 Holder 不等式2.22通过更换是1:
和(|X|)≤(和(|X|p))1/p, 在哪里 p≥1
经济代写|计量经济学代写ECONOMETRICS代考|MINKOWSKI’S INEQUALITY
如果对于一些p≥1,和[|X|p]<∞和和[|是|p]<∞, 然后和(|X+是|)≤(和(|X|p))1/p+(和(|是|p))1/p.这种不平等是由闵可夫斯基造成的。为了p=1结果是微不足道的。因此,让p>1. 首先请注意和[|X+是|p]≤和[(2⋅最大限度(|X|,|是|))p]= 2p和[最大限度(|X|p,|是|p)]≤2p和[|X|p+|是|p]<∞; 因此,我们可以应用 Liapounov 不等式:
和(|X+是|)≤(和(|X+是|p))1/p.
接下来,观察
和(|X+是|p)=和(|X+是|p−1|X+是|)≤和(|X+是|p−1|X|) +和(|X+是|p−1|是|).
让q=p/(p−1). 因为1/q+1/p=1由霍尔德不等式得出
和(|X+是|p−1|X|)≤(和(|X+是|(p−1)q))1/q(和(|X|p))1/p ≤(和(|X+是|p))1−1/p(和(|X|p))1/p
同样,
和(|X+是|p−1|是|)≤(和(|X+是|p))1−1/p(和(|是|p))1/p.
如果我们结合2.24-2.26, Minkowski 不等式2.23跟随。

经济代写|计量经济学代写Econometrics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。