如果你也在 怎样代写计量经济学Econometrics是将统计方法应用于经济数据,以赋予经济关系以经验内容。更确切地说,它是 “基于理论和观察的同步发展,通过适当的推理方法对实际经济现象进行定量分析”。 一本经济学入门教科书将计量经济学描述为允许经济学家 “从堆积如山的数据中筛选出简单的关系”。
计量经济学Econometrics的一个基本工具是多元线性回归模型。计量经济学理论使用统计理论和数理统计来评估和发展计量经济学方法。计量经济学家试图找到具有理想统计特性的估计器,包括无偏性、效率和一致性。应用计量经济学使用理论计量经济学和现实世界的数据来评估经济理论,开发计量经济学模型,分析经济历史和预测。
my-assignmentexpert™ 计量经济学Econometrics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的计量经济学Econometrics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计量经济学Econometrics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计量经济学Econometrics代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种计量经济学Econometrics相关的作业也就用不着 说。
我们提供的计量经济学Econometrics及其相关学科的代写,服务范围广, 其中包括但不限于:
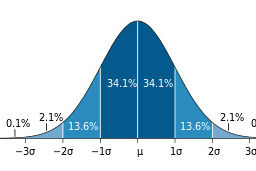
经济代写|计量经济学代写Econometrics代考|The Standard Normal Distribution
The standard normal distribution is an absolutely continuous distribution with density function
$$
f(x)=\frac{\exp \left(-x^{2} / 2\right)}{\sqrt{2 \pi}}, \quad x \in \mathbb{R} .
$$
Compare this equation with (4.27). Its moment-generating function is
$$
\begin{aligned}
m_{N(0,1)}(t) &=\int_{-\infty}^{\infty} \exp (t \cdot x) f(x) d x=\int_{-\infty}^{\infty} \exp (t \cdot x) \frac{\exp \left(-x^{2} / 2\right)}{\sqrt{2 \pi}} d x \
&=\exp \left(t^{2} / 2\right) \int_{-\infty}^{\infty} \frac{\exp \left[-\left(x^{2}-2 t \cdot x+t^{2}\right) / 2\right]}{\sqrt{2 \pi}} d x \
&=\exp \left(t^{2} / 2\right) \int_{-\infty}^{\infty} \frac{\exp \left[-(x-t)^{2} / 2\right]}{\sqrt{2 \pi}} d x \
&=\exp \left(t^{2} / 2\right) \int_{-\infty}^{\infty} \frac{\exp \left[-u^{2} / 2\right]}{\sqrt{2 \pi}} d u=\exp \left(t^{2} / 2\right)
\end{aligned}
$$
which exists for all $t \in \mathbb{R}$, and its characteristic function is
$$
\varphi_{N(0,1)}(t)=m(i \cdot t)=\exp \left(-t^{2} / 2\right)
$$
Consequently, if $X$ is standard normally distributed, then
$$
E[X]=\left.m^{\prime}(t)\right|{t=0}=0, E\left[X^{2}\right]=\operatorname{var}(X)=\left.m^{\prime \prime}(t)\right|{t=0}=1
$$
Given this result, the standard normal distribution is denoted by $N(0,1)$, where the first number is the expectation and the second number is the variance, and the statement ” $X$ is standard normally distributed” is usually abbreviated as ” $X \sim N(0,1) . “$
经济代写|计量经济学代写Econometrics代考|The General Normal Distribution
Now let $Y=\mu+\sigma X$, where $X \sim N(0,1)$. It is left as an easy exercise to verify that the density of $Y$ takes the form
$$
f(x)=\frac{\exp \left(-\frac{1}{2}(x-\mu)^{2} / \sigma^{2}\right)}{\sigma \sqrt{2 \pi}}, \quad x \in \mathbb{R}
$$
with corresponding moment-generating function
$$
m_{N\left(\mu, \sigma^{2}\right)}(t)=E[\exp (t \cdot Y)]=\exp (\mu t) \exp \left(\sigma^{2} t^{2} / 2\right), \quad t \in \mathbb{R}
$$
and characteristic function
$$
\varphi_{N\left(\mu, \sigma^{2}\right)}(t)=E[\exp (i \cdot t \cdot Y)]=\exp (i \cdot \mu t) \exp \left(-\sigma^{2} t^{2} / 2\right)
$$
Consequently, $E[Y]=\mu, \operatorname{var}(Y)=\sigma^{2}$. This distribution is the general normal distribution, which is denoted by $N\left(\mu, \sigma^{2}\right)$. Thus, $Y \sim N\left(\mu, \sigma^{2}\right)$.
计量经济学代写
经济代写|计量经济学代写ECONOMETRICS代考|THE STANDARD NORMAL DISTRIBUTION
标准正态分布是具有密度函数的绝对连续分布
F(X)=经验(−X2/2)2圆周率,X∈R.
将此等式与4.27. 它的矩生成函数是
米ñ(0,1)(吨)=∫−∞∞经验(吨⋅X)F(X)dX=∫−∞∞经验(吨⋅X)经验(−X2/2)2圆周率dX =经验(吨2/2)∫−∞∞经验[−(X2−2吨⋅X+吨2)/2]2圆周率dX =经验(吨2/2)∫−∞∞经验[−(X−吨)2/2]2圆周率dX =经验(吨2/2)∫−∞∞经验[−在2/2]2圆周率d在=经验(吨2/2)
为所有人而存在吨∈R, 其特征函数为
披ñ(0,1)(吨)=米(一世⋅吨)=经验(−吨2/2)
因此,如果X是标准正态分布,则
$$
EX=\left.m^{\素数}吨\对| {t=0}=0, E\左X^{2}\右X^{2}\右= \ 操作员名称 {var}X=\left.m^{\素数\素数}吨\对| {t=0}=1
$$
给定这个结果,标准正态分布表示为ñ(0,1),其中第一个数字是期望值,第二个数字是方差,语句 ”X是标准正态分布”通常缩写为“X∼ñ(0,1).“
经济代写|计量经济学代写ECONOMETRICS代考|THE GENERAL NORMAL DISTRIBUTION
现在让是=μ+σX, 在哪里X∼ñ(0,1). 留下一个简单的练习来验证密度是采取形式
F(X)=经验(−12(X−μ)2/σ2)σ2圆周率,X∈R
具有相应的力矩生成功能
米ñ(μ,σ2)(吨)=和[经验(吨⋅是)]=经验(μ吨)经验(σ2吨2/2),吨∈R
和特征函数
披ñ(μ,σ2)(吨)=和[经验(一世⋅吨⋅是)]=经验(一世⋅μ吨)经验(−σ2吨2/2)
最后,和[是]=μ,曾是(是)=σ2. 这种分布是一般的正态分布,表示为ñ(μ,σ2). 因此,是∼ñ(μ,σ2).

经济代写|计量经济学代写Econometrics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。