如果你也在 怎样代写计量经济学Econometrics是将统计方法应用于经济数据,以赋予经济关系以经验内容。更确切地说,它是 “基于理论和观察的同步发展,通过适当的推理方法对实际经济现象进行定量分析”。 一本经济学入门教科书将计量经济学描述为允许经济学家 “从堆积如山的数据中筛选出简单的关系”。
计量经济学Econometrics的一个基本工具是多元线性回归模型。计量经济学理论使用统计理论和数理统计来评估和发展计量经济学方法。计量经济学家试图找到具有理想统计特性的估计器,包括无偏性、效率和一致性。应用计量经济学使用理论计量经济学和现实世界的数据来评估经济理论,开发计量经济学模型,分析经济历史和预测。
my-assignmentexpert™ 计量经济学Econometrics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的计量经济学Econometrics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计量经济学Econometrics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计量经济学Econometrics代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种计量经济学Econometrics相关的作业也就用不着 说。
我们提供的计量经济学Econometrics及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|计量经济学代写Econometrics代考|Introduction
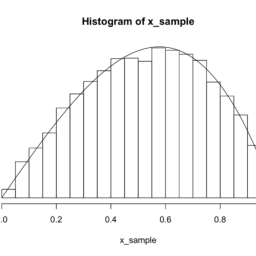
Fill a bowl with ten balls numbered from 0 to 9 . Draw a ball randomly from this bowl and write down the corresponding number as the first decimal digit of a number between 0 and 1 . For example, if the first-drawn number is 4 , then write down 0.4. Put the ball back in the bowl, and repeat this experiment. If, for example, the second ball corresponds to the number 9 , then this number becomes the second decimal digit: $0.49$. Repeating this experiment infinitely many times yields a random number between 0 and 1 . Clearly, the sample space involved is the unit interval: $\Omega=[0,1]$.
For a given number $x \in[0,1]$ the probability that this random number is less than or equal to $x$ is $x$. To see this, suppose that you only draw two balls and that $x=0.58$. If the first ball has a number less than 5 , it does not matter what the second number is. There are five ways to draw a first number less than or equal to 4 and 10 ways to draw the second number. Thus, there are 50 ways to draw a number with a first digit less than or equal to 4 . There is only one way to draw a first number equal to 5 and 9 ways to draw a second number less than or equal to 8 . Thus, the total number of ways we can generate a number less than or equal to $0.58$ is 59 , and the total number of ways we can draw two numbers with replacement is 100 . Therefore, if we only draw two balls with replacement and use the numbers involved as the first and second decimal digit, the probability that we will obtain a number less than or equal to $0.58$ is $0.59$. Similarly, if we draw 10 balls with replacement, the probability that we will obtain a number less than or equal to $0.5831420385$, for instance, is $0.5831420386$. In the limit the difference between $x$ and the corresponding probability disappears. Thus, for $x \in[0,1]$ we have $P([0, x])=x$. By the same argument it follows that for $x \in[0,1], P({x})=P([x, x])=0$, that is, the probability that the random number involved will be exactly equal to a given number $x$ is zero. Therefore, for a given $x \in[0,1], P((0, x])=P([0, x))=P((0, x))=x$. More generally, for any interval in $[0,1]$ the corresponding probability is the length of the interval involved regardless of whether the endpoints are included. Thus, for $0 \leq a<$ $b \leq 1$, we have $P([a, b])=P((a, b])=P([a, b))=P((a, b))=b-a$. Any finite union of intervals can be written as a finite union of disjoint intervals by cutting out the overlap. Therefore, this probability measure extends to finite unions of intervals simply by adding up the lengths of the disjoint intervals involved. Moreover, observe that the collection of all finite unions of subintervals in $[0,1]$, including $[0,1]$ itself and the empty set, is closed under the formation of complements and finite unions. Thus, we have derived the probability measure $P$ corresponding to the statistical experiment under review for an algebra $\mathscr{F}_{0}$ of subsets of $[0,1]$, namely,
$$
\mathscr{F}_{0}={(a, b),[a, b],(a, b],[a, b), \forall a, b \in[0,1], a \leq b,
$$
and their finite unions $}$,
where $[a, a]$ is the singleton ${a}$ and each of the sets $(a, a),(a, a]$ and $[a, a)$ should be interpreted as the empty set $\emptyset$. This probability measure is a special case of the Lebesgue measure, which assigns each interval its length.
If you are only interested in making probability statements about the sets in the algebra (1.20), then you are done. However, although the algebra (1.20) contains a large number of sets, we cannot yet make probability statements involving arbitrary Borel sets in $[0,1]$ because not all the Borel sets in $[0,1]$ are included in (1.20). In particular, for a countable sequence of sets $A_{j} \in \mathscr{F}{0}$, the probability $P\left(\cup{j=1}^{\infty} A_{j}\right)$ is not always defined because there is no guarantee that $\cup_{j=1}^{\infty} A_{j} \in \mathscr{F}{0}$. Therefore, to make probability statements about arbitrary Borel set in $[0,1]$, you need to extend the probability measure $P$ on $\mathscr{F}{0}$ to a probability measure defined on the Borel sets in $[0,1]$. The standard approach to do this is to use the outer measure.
经济代写|计量经济学代写Econometrics代考|Outer Measure
infinite union of sets in the algebra $\mathscr{F}{0}: A \subset \cup{j=1}^{\infty} A_{j}$, where $A_{j} \in \mathscr{F}{0}$; hence, the “probability” of $A$ is bounded from above by $\sum{j=1}^{\infty} P\left(A_{j}\right)$. Taking the infimum of $\sum_{j=1}^{\infty} P\left(A_{j}\right)$ over all countable sequences of sets $A_{j} \in \mathscr{F}{0}$ such that $A \subset \cup{j=1}^{\infty} A_{j}$ then yields the outer measure:
Definition 1.7: Let $\mathscr{F}{0}$ be an algebra of subsets of $\Omega$. The outer measure of an arbitrary subset $A$ of $\Omega$ is $$ P^{}(A)=\inf {A \subset \cup_{j=1}^{\infty} A_{j}, A_{j} \in \mathcal{F}{0}} \sum{j=1}^{\infty} P\left(A_{j}\right) .
$$
Note that it is not required in (1.21) that $\cup_{j=1}^{\infty} A_{j} \in \mathscr{F}{0}$. Because a union of sets $A{j}$ in an algebra $\mathscr{F}{0}$ can always be written as a union of disjoint sets in the algebra $\mathscr{F}{0}$ (see Theorem 1.4), we may without loss of generality assume that the infimum in (1.21) is taken over all disjoint sets $A_{j}$ in $\mathscr{F}{0}$ such that $A \subset \cup{j=1}^{\infty} A_{j}$. This implies that
If $A \in \mathscr{F}_{0}$ then $P^{}(A)=P(A)$.
The question now arises, For which other subsets of $\Omega$ is the outer measure a probability measure? Note that the conditions (1.8) and (1.9) are satisfied for the outer measure $P^{*}$ (Exercise: Why?), but, in general, condition (1.10) does not
hold for arbitrary sets. See, for example, Royden $(1968,63-64)$. Nevertheless, it is possible to extend the outer measure to a probability measure on a $\sigma$-algebra $\mathscr{F}$ containing $\mathscr{F}_{0}$ :
Theorem 1.9: Let $P$ be a probability measure on $\left{\Omega, \mathscr{F}{0}\right}$, where $\mathscr{F}{0}$ is an algebra, and let $\mathscr{F}=\sigma\left(\mathscr{F}{0}\right)$ be the smallest $\sigma$-algebra containing the algebra $\mathscr{F}{0}$. Then the outer measure $P^{*}$ is a unique probability measure on ${\Omega, \mathscr{F}}$, which coincides with $P$ on $\mathscr{F}_{0}$.
计量经济学代写
经济代写|计量经济学代写ECONOMETRICS代考|INTRODUCTION
将编号为 0 到 9 的十个球装满一个碗。从这个碗里随机抽一个球,写下相应的数字作为 0 到 1 之间数字的第一个小数位。例如,如果第一个绘制的数字是 4 ,则记下 0.4。把球放回碗里,重复这个实验。例如,如果第二个球对应于数字 9 ,那么这个数字将成为第二个十进制数字:0.49. 无限次重复这个实验会产生一个介于 0 和 1 之间的随机数。显然,所涉及的样本空间是单位区间:Ω=[0,1].
对于给定的数字X∈[0,1]这个随机数小于或等于的概率X是X. 要看到这一点,假设您只画了两个球,并且X=0.58. 如果第一个球的数字小于 5 ,则第二个数字是什么无关紧要。有五种方法可以绘制小于或等于 4 的第一个数字,以及 10 种绘制第二个数字的方法。因此,有 50 种方法可以绘制第一位小于或等于 4 的数字。只有一种方法可以得出第一个等于 5 的数字,而 9 种方法可以得出第二个小于或等于 8 的数字。因此,我们可以生成小于或等于的数字的方法总数0.58是 59 ,我们可以用替换画出两个数字的方法总数是 100 。因此,如果我们只抽出两个有放回的球,并将所涉及的数字作为小数点后的第一位和第二位,我们得到一个小于或等于的数字的概率为0.58是0.59. 类似地,如果我们抽出 10 个有放回的球,我们得到一个小于或等于的数字的概率为0.5831420385,例如,是0.5831420386. 在极限之间的差异X相应的概率就消失了。因此,对于X∈[0,1]我们有磷([0,X])=X. 根据同样的论点,对于X∈[0,1],磷(X)=磷([X,X])=0,即所涉及的随机数与给定数完全相等的概率X为零。因此,对于给定的X∈[0,1],磷((0,X])=磷([0,X))=磷((0,X))=X. 更一般地,对于任何间隔[0,1]相应的概率是所涉及的区间的长度,无论是否包括端点。因此,对于0≤一种< b≤1, 我们有磷([一种,b])=磷((一种,b])=磷([一种,b))=磷((一种,b))=b−一种. 通过去除重叠,任何区间的有限并集都可以写成不相交区间的有限并集。因此,这种概率度量仅通过将所涉及的不相交区间的长度相加即可扩展到有限的区间联合。此外,观察到子区间的所有有限并集的集合[0,1], 包含[0,1]自身和空集在补集和有限联合的形成下是封闭的。因此,我们推导出了概率测度磷对应于代数审查中的统计实验F0的子集[0,1],即,
$$
\mathscr{F}_{0}={一种,b,一种,b,一种,b],[一种,b, \forall a, b \in0,1, a \leq b,
$$
和它们的有限并集}},
其中[一种,一种]是单身人士一种和每一组(一种,一种),(一种,一种]和[一种,一种)应该被解释为空集∅. 这个概率测度是 Lebesgue 测度的一个特例,它为每个区间分配了它的长度。
如果您只想对代数中的集合进行概率陈述1.20,那么你就完成了。然而,虽然代数1.20包含大量集合,我们还不能做出涉及任意 Borel 集合的概率陈述[0,1]因为不是所有的 Borel 都进入[0,1]包含在1.20. 特别是,对于集合的可数序列$[0,1]$ because not all the Borel sets in $[0,1]$ are included in (1.20). In particular, for a countable sequence of sets $A_{j} \in \mathscr{F}{0}$, the probability $P\left(\cup{j=1}^{\infty} A_{j}\right)$ is not always defined because there is no guarantee that $\cup_{j=1}^{\infty} A_{j} \in \mathscr{F}{0}$. Therefore, to make probability statements about arbitrary Borel set in $[0,1]$, you need to extend the probability measure $P$ on $\mathscr{F}{0}$。执行此操作的标准方法是使用外部度量。
经济代写|计量经济学代写ECONOMETRICS代考|OUTER MEASURE
代数中集合的无限并集 $\mathscr{F} {0}: A \subset \cup {j=1}^{\infty} A_{j},在H和r和A_{j} \in \mathscr{F} {0};H和nC和,吨H和“pr这b一种b一世l一世吨是”这F一种一世sb这在nd和dFr这米一种b这在和b是\sum {j=1}^{\infty} P\leftA_{j}\右A_{j}\右.吨一种ķ一世nG吨H和一世nF一世米在米这F\sum_{j=1}^{\infty} P\leftA_{j}\右A_{j}\右这在和r一种llC这在n吨一种bl和s和q在和nC和s这Fs和吨sA_{j} \in \mathscr{F} {0}s在CH吨H一种吨A \subset \cup {j=1}^{\infty} A_{j}$ 然后产生外部度量:
定义 1.7:设 $\mathscr{F}{0}$ be an algebra of subsets of $\Omega$. The outer measure of an arbitrary subset $A$ of $\Omega$ is $$ P^{}(A)=\inf {A \subset \cup_{j=1}^{\infty} A_{j}, A_{j} \in \mathcal{F}{0}} \sum{j=1}^{\infty} P\left(A_{j}\right) .
$$
Note that it is not required in (1.21) that $\cup_{j=1}^{\infty} A_{j} \in \mathscr{F}{0}$. Because a union of sets $A{j}$ in an algebra $\mathscr{F}{0}$ can always be written as a union of disjoint sets in the algebra $\mathscr{F}{0}$ (see Theorem 1.4), we may without loss of generality assume that the infimum in (1.21) is taken over all disjoint sets $A_{j}$ in $\mathscr{F}{0}$ such that $A \subset \cup{j=1}^{\infty} A_{j}$. This implies that
If $A \in \mathscr{F}_{0}$ then $P^{}(A)=P(A)$., 但一般情况下1.10才不是
持有任意集合。参见,例如,罗伊登(1968,63−64). 然而,有可能将外部测量扩展到一个概率测量σ-代数F包含F0:
定理 1.9:让磷是$\left{\Omega, \mathscr{F}{0}\right}$, where $\mathscr{F}{0}$ is an algebra, and let $\mathscr{F}=\sigma\left(\mathscr{F}{0}\right)$ be the smallest $\sigma$-algebra containing the algebra $\mathscr{F}{0}$. Then the outer measure $P^{*}$ is a unique probability measure on ${\Omega, \mathscr{F}}$, which coincides with $P$ on $\mathscr{F}_{0}$.

经济代写|计量经济学代写Econometrics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。