如果你也在 怎样代写拓扑学topology这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。拓扑学topology在数学中,拓扑学(来自希腊语中的τόπος,”地方、位置”,和λόγος,”研究”)关注的是几何对象在连续变形下保持的属性,如拉伸、扭曲、皱缩和弯曲;也就是说,在不关闭孔、打开孔、撕裂、粘连或穿过自身的情况下。
拓扑学topology拓扑空间是一个被赋予了结构的集合,称为拓扑,它允许定义子空间的连续变形,以及更广泛地定义所有种类的连续性。欧几里得空间,以及更一般的,公制空间都是拓扑空间的例子,因为任何距离或公制都定义了一个拓扑。拓扑学中所考虑的变形是同构和同形。在这种变形下不变的属性是一种拓扑属性。拓扑属性的基本例子有:维度,它可以区分线和面;紧凑性,它可以区分线和圆;连接性,它可以区分一个圆和两个不相交的圆。
my-assignmentexpert™ 拓扑学topology作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的拓扑学topology作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此拓扑学topology作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的拓扑学topology代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种拓扑学topology相关的作业也就用不着 说。
我们提供的拓扑学topology及其相关学科的代写,服务范围广, 其中包括但不限于:
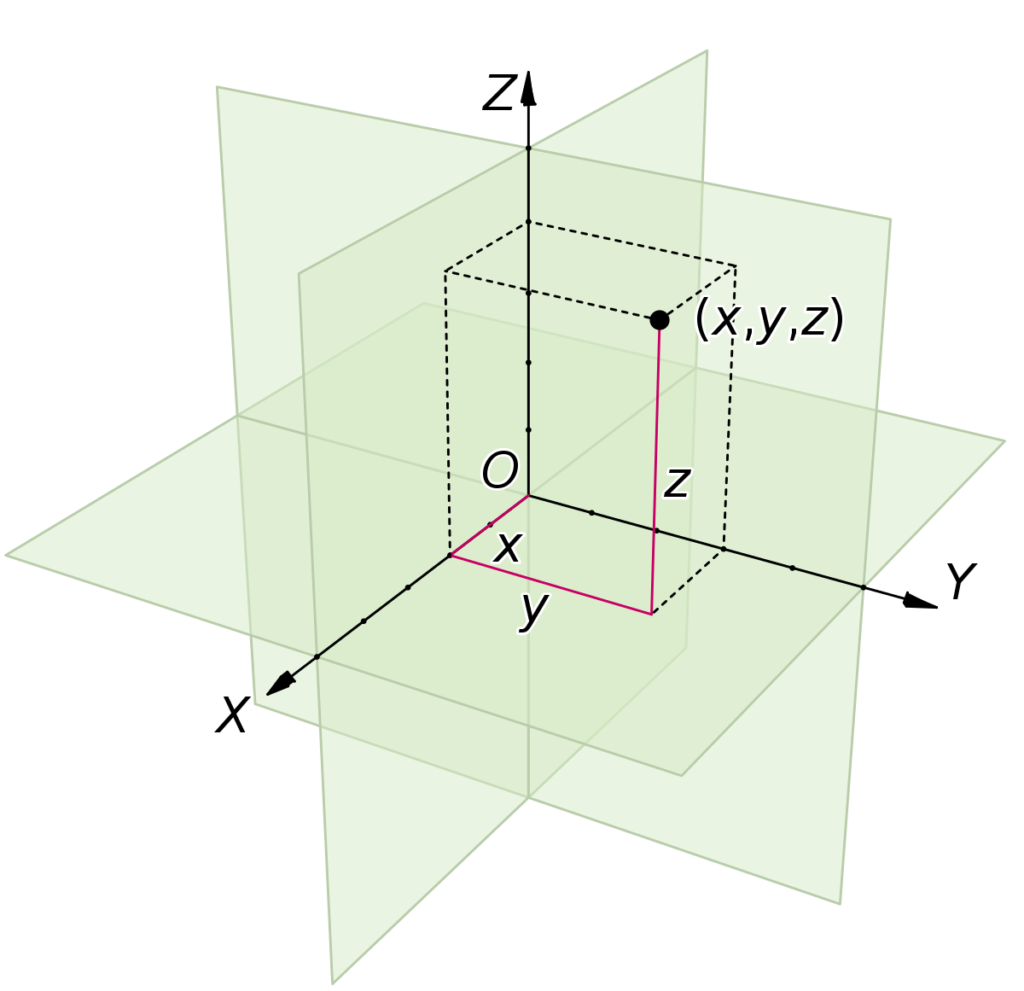
数学代写|拓扑学作业代写topology代考|Basic structures on Rn
Every space $\mathbb{R}^{n}, n \in \mathbb{N}$, is endowed with a variety of structures that will be employed case by case.
$\mathbb{R}^{n}$ is the vector space of column vectors (with $n$ rows). We stipulate that if $v \in \mathbb{R}^{n}$ occurs as a vector in any linear algebra formula, then it is considered as a column.
The space $\mathcal{L}\left(\mathbb{R}^{n}, \mathbb{R}^{m}\right)$ of linear maps $L: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ coincides with the space of $m \times n$ matrices, $M(m, n, \mathbb{R})$, so that for every $v \in \mathbb{R}^{n}, v \rightarrow L v$ via the usual “rows by column” product. Using the lexicographic order on the entries of any matrix $L=\left(l_{i, j}\right)_{i=1, \ldots, m ; j=1, \ldots, n}$, we also fix the identification of $M(m, n, \mathbb{R})$ with $\mathbb{R}^{m n}$.
As with every vector space, $\mathbb{R}^{n}$ has a canonical structure of affine space over itself determined by the map that associates to every pair of points $(x, y) \in \mathbb{R}^{n} \times \mathbb{R}^{n}$ the vector $\overrightarrow{x y}:=y-x$. Every element of $\mathbb{R}^{n}$ can be considered either as a point $x$ of the space or as a vector $v$. For every point $x$ and every vector $v$, there is a unique point $y:=x+v$ such that $v=\overrightarrow{x y}$; for every point $x$, the map $v \rightarrow x+v$ is a bijection. Consider $T\left(\mathbb{R}^{n}\right):=\mathbb{R}^{n} \times \mathbb{R}^{n}$ where the first (second) factor consists of points (vectors) and the natural projection onto the space factor $\pi_{n}: T\left(\mathbb{R}^{n}\right) \rightarrow \mathbb{R}^{n}, \pi_{n}(x, v)=x$. For every point $x$, the fibre $T_{x} \mathbb{R}^{n}=\pi^{-1}(x)$ is a copy of the vector space $\mathbb{R}^{n}$, called the tangent vector space to the affine space at the point $x$. We call $\left(T\left(\mathbb{R}^{n}\right), \pi_{n}\right)$ the affine tangent vector bundle of the affine space $\mathbb{R}^{n}$. The space of points $\mathbb{R}^{n}$ can be included in $T\left(\mathbb{R}^{n}\right)$ via the zero section $s_{0}(x)=(x, 0)$, so that for every point $x, \pi \circ s_{0}(x)=x$. For every affine map $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$, there is a unique linear map $L_{f}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$, called the linear part of the affine map, such that for every point $x$ and every vector $v, f(x+v)=f(x)+L_{f} v$. The map $f$ is an affine isomorphism if and only if $L_{f}$ is a linear isomorphism (in such a case, $n=m)$. In other words, the tangent map of $f$,
$$
T f:=\left(f, L_{f}\right): \mathbb{R}^{n} \times \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} \times \mathbb{R}^{m},(x, v) \rightarrow\left(f(x), L_{f} v\right),
$$
verifies $\pi_{m} \circ T f=f \circ \pi_{n}$, so that for every point $x$, the tangent space $T_{x} \mathbb{R}^{n}$ goes to the tangent space $T_{f(x)} \mathbb{R}^{m}$ via the linear map $L_{f}$.
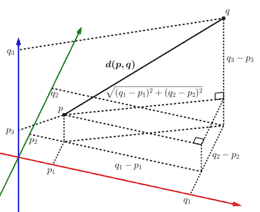
$\mathbb{R}^{n}$ is a complete metric space endowed with the Euclidean distance $d=$ $d_{n}$ defined by
$$
d(x, y)=\sqrt{\sum_{j=1}^{n}\left(x_{j}-y_{j}\right)^{2}}
$$
The standard positive definite scalar product $(*, *)=(*, *){n}$ on $\mathbb{R}^{n}$ is defined by $$ (x, y):=\sum{j=1}^{n} x_{j} y_{j}=x^{t} I y
$$
with the associated norm $|x|=\sqrt{(x, x)}$. We note that
$$
d^{2}(x, y)=(x-y, x-y)
$$
and that the familiar formula
$$
(x, y)=|x| \cdot|y| \cos \theta
$$
allows us to recover the measure of the angle formed by the ordered and oriented lines spanned by two nonzero vectors $x, y$; in particular, they are orthogonal iff $(x, y)=0$. We see that many basic objects of elementary geometry can be expressed analytically using the standard scalar product.
数学代写|拓扑学作业代写topology代考|Differential calculus
Another fundamental structure carried by the spaces $\mathbb{R}^{n}$ is the differential calculus. Let $U \subset \mathbb{R}^{n}, W \subset \mathbb{R}^{m}$ be open sets. A map
$$
f=\left(f_{1}, \ldots, f_{m}\right): U \rightarrow W
$$
is said to be $\mathcal{C}^{0}$ if it is continuous. The map is differentiable at $x \in U$ if there is a (necessarily unique) linear map $d_{x} f \in \mathcal{L}\left(\mathbb{R}^{n}, \mathbb{R}^{m}\right)$ that “well” approximates $g(h)=f(x+h)-f(x)$ in a neighbourhood of $h=0$. Precisely, for every $\epsilon>0$, there is $\delta>0$ such that for every $h$ such that $|h|<\delta$, $x+h \in U$ and
$$
\left|g(h)-d_{x} f(h)\right| \leq \epsilon|h| .
$$
The linear map $d_{x} f$ is called the differential of $f$ at $x$. The map $f$ is (globally) differentiable if it is differentiable at every point $x \in U$. In such a case it is defined as the differential map
$$
d f: U \rightarrow M(m, n, \mathbb{R}), d f(x):=d_{x} f \text {. }
$$
We say $f$ is $\mathcal{C}^{1}$ if it is differentiable and $d f$ is continuous (being $M(m, n, \mathbb{R})$, that is, $\mathcal{L}\left(\mathbb{R}^{n}, \mathbb{R}^{m}\right)$, identified with $\mathbb{R}^{m n}$ as we said above). Every $\mathcal{C}^{1}$-map is $\mathcal{C}^{0}$. By induction, for every $r \geq 1$, we say that $f$ is $\mathcal{C}^{r}$ if $d f$ is $\mathcal{C}^{r-1}$. In practice, $f$ is $\mathcal{C}^{r}, r \geq 1$, if and only if it is $\mathcal{C}^{0}$ and for every multi-index $J=j_{1} \ldots j_{n}$ of order $|J|:=j_{1}+\cdots+j_{m} \leq r$, for every $i=1, \ldots, m$, the partial derivative function
$$
\frac{\partial^{J} f_{i}}{\partial^{j_{1}} x_{1} \ldots \partial^{j_{n}} x_{n}}: U \rightarrow \mathbb{R}
$$
is defined and continuous. For every $x \in U$, the partial derivatives of the first order can be organized in an $m \times n$ matrix so that
$$
d_{x} f:=\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)_{i=1, \ldots, m ; j=1, \ldots, n} \in M(m, n, \mathbb{R})
$$
A map $f$ is $\mathcal{C}^{\infty}$ or, equivalently, smooth if it is $\mathcal{C}^{r}$ for every $r \geq 0$. If $f$ is smooth, then $d f$ is also smooth. So we can define inductively for every $r \geq 1, d^{r} f=d\left(d^{r-1} f\right) .$
If $f$ is (at least) $\mathcal{C}^{1}$, we have the following uniform version of the above property that defines the differentials $d_{x} f$ : for every $x \in U$ there exists a neighbourhood $W$ of $x$ in $U$ (we can take as $W$ a compact closed ball $\left.\bar{B}^{n}(x, \rho) \subset U\right)$, such that for every $\epsilon>0$, there is $\delta>0$ such that for every $y \in W$ and for every $h,|h|<\delta$, we have $y+h \in U$ and
$$
\left.| f(y+h)-f(y)-d_{y} f(h)\right) | \leq \epsilon \delta ;
$$
in other words,
$$
\lim {h \rightarrow 0} \frac{g(y, h)-d{y} f(h)}{|h|}=0
$$
uniformly on $W$.
From now on we will deal mainly with smooth maps.
数学代写|拓扑学作业代写TOPOLOGY代考|An elementary division theorem
By definition, a convex subset $C$ of $\mathbb{R}^{n}$ has the property that for every $x_{0}, x_{1} \in C$, the (parametric) segment $\gamma:[0,1] \rightarrow \mathbb{R}^{n}, \gamma(t)=(1-t) x_{0}+t x_{1}$ is entirely contained in $C$.
Theorem $1.2$ (Elementary division theorem). Let $f=\left(f_{1}, \ldots, f_{m}\right) \in$ $\mathcal{C}^{\infty}\left(U, \mathbb{R}^{m}\right)$ where $U \subset \mathbb{R}^{n}$ is a convex open subset. Assume that $0 \in U$ and $f(0)=0$. Then there are smooth maps $g_{j}=\left(g_{j 1}, \ldots, g_{j m}\right): U \rightarrow \mathbb{R}^{m}$, $j=1, \ldots, n$, such that for every $x \in U, f(x)=\sum_{j} x_{j} g_{j}(x)$ and (necessarily) $g_{j i}(0)=\frac{\partial f_{i}}{\partial x_{j}}(0)$.
拓扑学代写
数学代写|拓扑学作业代写TOPOLOGY代考|BASIC STRUCTURES ON RN
每个空间Rn,n∈ñ, 具有多种结构,将逐案采用。
Rn是列向量的向量空间在一世吨H$n$r这在s. 我们规定如果在∈Rn在任何线性代数公式中作为向量出现,则它被视为一列。
空间大号(Rn,R米)线性映射大号:Rn→R米与空间相吻合米×n矩阵,米(米,n,R),所以对于每个在∈Rn,在→大号在通过通常的“逐列行”产品。对任何矩阵的条目使用字典顺序大号=(l一世,j)一世=1,…,米;j=1,…,n,我们还修复了米(米,n,R)和R米n.
与每个向量空间一样,Rn在其自身上具有仿射空间的规范结构,由关联到每对点的映射确定(X,是)∈Rn×Rn向量X是→:=是−X. 的每一个元素Rn可以被认为是一个点X空间的或作为向量在. 对于每一点X和每个向量在, 有一个独特的点是:=X+在这样在=X是→; 对于每一点X, 地图在→X+在是双射。考虑吨(Rn):=Rn×Rn第一个在哪里s和C这nd因子由点组成在和C吨这rs以及对空间因子的自然投影圆周率n:吨(Rn)→Rn,圆周率n(X,在)=X. 对于每一点X, 纤维吨XRn=圆周率−1(X)是向量空间的副本Rn,称为该点处的仿射空间的切向量空间X. 我们称之为(吨(Rn),圆周率n)仿射空间的仿射切向量丛Rn. 点的空间Rn可以包含在吨(Rn)通过零部分s0(X)=(X,0), 所以对于每一点X,圆周率∘s0(X)=X. 对于每个仿射图F:Rn→R米, 存在唯一的线性映射大号F:Rn→R米,称为仿射图的线性部分,使得对于每个点X和每个向量在,F(X+在)=F(X)+大号F在. 地图F是仿射同构当且仅当大号F是线性同构一世ns$$
T f:=\left(f, L_{f}\right): \mathbb{R}^{n} \times \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} \times \mathbb{R}^{m},(x, v) \rightarrow\left(f(x), L_{f} v\right),
$$
verifies $\pi_{m} \circ T f=f \circ \pi_{n}$, so that for every point $x$, the tangent space $T_{x} \mathbb{R}^{n}$ goes to the tangent space $T_{f(x)} \mathbb{R}^{m}$ via the linear map $L_{f}$.
$\mathbb{R}^{n}$ is a complete metric space endowed with the Euclidean distance $d=$ $d_{n}$ defined by
$$
d(x, y)=\sqrt{\sum_{j=1}^{n}\left(x_{j}-y_{j}\right)^{2}}
$$
The standard positive definite scalar product $(*, *)=(*, *){n}$ on $\mathbb{R}^{n}$ is defined by $$ (x, y):=\sum{j=1}^{n} x_{j} y_{j}=x^{t} I y
$$
with the associated norm $|x|=\sqrt{(x, x)}$. We note that
$$
d^{2}(x, y)=(x-y, x-y)
$$
and that the familiar formula
$$
(x, y)=|x| \cdot|y| \cos \theta
$$
允许我们恢复由两个非零向量跨越的有序和定向线形成的角度的度量X,是; 特别是,它们是正交 iff(X,是)=0. 我们看到,许多基本几何的基本对象都可以用标准的标量积来解析地表达。
数学代写|拓扑学作业代写TOPOLOGY代考|DIFFERENTIAL CALCULUS
空间承载的另一个基本结构Rn是微积分。让在⊂Rn,在⊂R米是开集。一张地图
F=(F1,…,F米):在→在
据说是C0如果是连续的。地图是可微分的X∈在如果有一个n和C和ss一种r一世l是在n一世q在和线性地图dXF∈大号(Rn,R米)那个“好”近似G(H)=F(X+H)−F(X)在附近H=0. 准确地说,对于每个ε>0, 有d>0这样对于每个H这样|H|<d, X+H∈在和
|G(H)−dXF(H)|≤ε|H|.
线性地图dXF被称为微分F在X. 地图F是Gl这b一种ll是可微的,如果它在每一点都是可微的X∈在. 在这种情况下,它被定义为差分图
dF:U \rightarrow M(m, n, \mathbb{R}), d f(x):=d_{x} f \text {. }
$$
We say $f$ is $\mathcal{C}^{1}$ if it is differentiable and $d f$ is continuous (being $M(m, n, \mathbb{R})$, that is, $\mathcal{L}\left(\mathbb{R}^{n}, \mathbb{R}^{m}\right)$, identified with $\mathbb{R}^{m n}$ as we said above). Every $\mathcal{C}^{1}$-map is $\mathcal{C}^{0}$. By induction, for every $r \geq 1$, we say that $f$ is $\mathcal{C}^{r}$ if $d f$ is $\mathcal{C}^{r-1}$. In practice, $f$ is $\mathcal{C}^{r}, r \geq 1$, if and only if it is $\mathcal{C}^{0}$ and for every multi-index $J=j_{1} \ldots j_{n}$ of order $|J|:=j_{1}+\cdots+j_{m} \leq r$, for every $i=1, \ldots, m$, the partial derivative function
$$
\frac{\partial^{J} f_{i}}{\partial^{j_{1}} x_{1} \ldots \partial^{j_{n}} x_{n}}: U \rightarrow \mathbb{R}
$$
is defined and continuous. For every $x \in U$, the partial derivatives of the first order can be organized in an $m \times n$ matrix so that
$$
d_{x} f:=\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)_{i=1, \ldots, m ; j=1, \ldots, n} \in M(m, n, \mathbb{R})
$$
一张地图F是C∞或者,等效地,如果它是平滑的Cr对于每个r≥0. 如果F是光滑的,那么dF也很顺利。所以我们可以归纳地定义每个r≥1,drF=d(dr−1F).
如果F是一种吨l和一种s吨 C1,我们有以下定义差异的上述属性的统一版本dXF: 对于每个X∈在有一个社区在的X在在 我们可以将一个紧凑的封闭球 $\left.\bar{B}^{n}(x, \rho我们可以将一个紧凑的封闭球 $\left.\bar{B}^{n}(x, \rho\subset U\right),s在CH吨H一种吨F这r和在和r是ε>0,吨H和r和一世s\delta>0s在CH吨H一种吨F这r和在和r是y \in W一种ndF这r和在和r是h,|h|<\delta,在和H一种在和y+h \in U一种nd|F(是+H)−F(是)−d是F(H))|≤εd;一世n这吨H和r在这rds,$
\lim {h \rightarrow 0} \frac{g是,H-d {y} fH}{|h|}=0
$$
一致在.
从现在开始,我们将主要处理平滑地图。
数学代写|拓扑学作业代写TOPOLOGY代考|AN ELEMENTARY DIVISION THEOREM
根据定义,凸子集C的Rn拥有对每个人来说X0,X1∈C, 这p一种r一种米和吨r一世C分割C:[0,1]→Rn,C(吨)=(1−吨)X0+吨X1完全包含在C.
定理1.2 $ (Elementary division theorem). Let $f=\left(f_{1}, \ldots, f_{m}\right) \in$ $\mathcal{C}^{\infty}\left(U, \mathbb{R}^{m}\right)$ where $U \subset \mathbb{R}^{n}$ is a convex open subset. Assume that $0 \in U$ and $f(0)=0$. Then there are smooth maps $g_{j}=\left(g_{j 1}, \ldots, g_{j m}\right): U \rightarrow \mathbb{R}^{m}$, $j=1, \ldots, n$, such that for every $x \in U, f(x)=\sum_{j} x_{j} g_{j}(x)$ and (necessarily) $g_{j i}(0)=\frac{\partial f_{i}}{\partial x_{j}}(0)$.

数学代写|拓扑学作业代写TOPOLOGY代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。