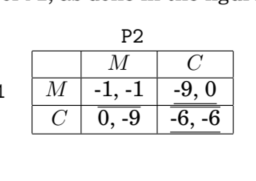
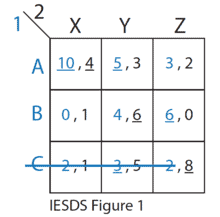
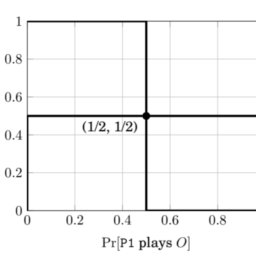
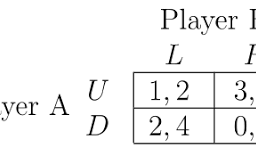
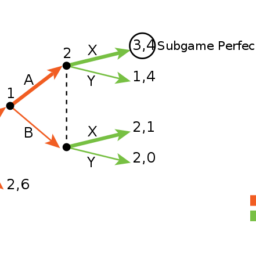
如果你也在 怎样代写博弈论game theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。博弈论game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域,以及逻辑学、系统科学和计算机科学中都有应用。最初,它针对的是两人的零和博弈,其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪,博弈论适用于广泛的行为关系;它现在是人类、动物以及计算机的逻辑决策科学的一个总称。
博弈论game theory在20世纪50年代被许多学者广泛地发展。虽然类似的发展至少可以追溯到1930年代,但它在1970年代被明确地应用于进化论。博弈论已被广泛认为是许多领域的重要工具。截至2020年,随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊,已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。
my-assignmentexpert™ 博弈论game theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的博弈论game theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此博弈论game theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济Economy作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的博弈论game theory代写服务。我们的专家在经济Economy代写方面经验极为丰富,各种博弈论game theory相关的作业也就用不着 说。
我们提供的博弈论game theory及其相关学科的代写,服务范围广, 其中包括但不限于:
经济代写|博弈论作业代写game theory代考|Characteristics
In this class of games, some or all players are associated with a set of types. The concept of type is used to represent the incompleteness of the information that one player may have about the others. The general assumption is that players know their own types but may only estimate the types of other players. Actually, this uncertainty may only involve some players; players that can have different types unknown to the others are called “Bayesian” like the games themselves. While types can be used to differentiate any aspect of the gameplay (including the way by which a dynamic game unfolds), they are most commonly employed to describe possible payoff functions for a player. One such player P can use different payoff functions $u_{\mathrm{A}}(\cdot), u_{\mathrm{B}}(\cdot), u_{\mathrm{C}}(\cdot), \ldots$ representing different preference orders he puts on the possible outcomes, which is represented by its type being $\mathrm{A}, \mathrm{B}, \mathrm{C}$, and so on. This, in turn, actually means that the other players are uncertain about what alternatives are preferred by player $P$, if the exact type of $P$ is known to P only.
Generally, the assignment of types to players is represented as a decision blindly made by the virtual non-rational player Nature that chooses them as random variables following a probability distribution. In principle, we should consider the joint distribution of all the types, denoted as $p\left(t_{1}, t_{2}, \ldots, t_{\mathrm{N}}\right)$ for all players $1,2, \ldots, \mathrm{N}$, where $t_{J}$ is the type of player $\mathrm{J}$. However, it is very frequent to assume that types are drawn independently for each player with a type, so that we can just use marginal distributions $p_{1}\left(t_{1}\right), p_{2}\left(t_{2}\right), \ldots, p_{\mathrm{N}}\left(t_{\mathrm{N}}\right)$ for players 1 , $2, \ldots, N$, respectively, where
$$
p\left(t_{1}, t_{2}, \ldots, t_{\mathrm{N}}\right)=p_{1}\left(t_{1}\right) \cdot p_{2}\left(t_{2}\right) \cdots \cdots p_{\mathrm{N}}\left(t_{\mathrm{N}}\right) .
$$
While from a general perspective, in very special cases it may make sense to assume some correlation among the types, and therefore negate the independence of types, in reality independence is often assumed for tractability reasons, and also for the sake of realism, since the entire game only comprises two players (and possibly only one with a type). Thus, after drawing the types, Nature also reveals the type $t_{\mathrm{J}}$ to player $\mathrm{J}$ only.
经济代写|博弈论作业代写GAME THEORY代考|Relevant cases
The general framework of Bayesian games can be specified to many different contexts. In particular, the solution concept used for each of these cases may change. The straightforward extension of Nash equilibrium to the Bayesian case is known as Bayesian Nash equilibrium (BNE) and it is nothing but a standard NE for a Bayesian game (which, according to the previous discussion, can be promptly translated into a dynamic game). However, similar to dynamic games, such a concept may often be insufficient to capture the rational behavior of the players in a credible way and obtain satisfactory predictions.
If the game simply implies a preliminary move of Nature for choosing the types of all involved players, and after that all choices of the players happen simultaneously, we can regard this as a static Bayesian game. Actually, the name is somehow misleading since it is not really a static game (there is a player, i.e., Nature, moving prior to the others). However, it is just a straightforward extension of static games of complete information, and since the type agent representation allows to remove the incompleteness of information, the BNE is more than enough to represent this case.
If the game is dynamic instead (and not just because of Nature’s preliminary move), then the solution concept becomes more complex, and also the strategies available to the players may explode, since they jointly account for multiple types and different rounds of gameplay. Generally, it is tractable to manually investigate scenarios with just 2 players, only one of which is Bayesian, and only allowing two rounds of interaction.
This leads to the following relevant cases, for which the solution approach is somewhat standardized. The first is the case of a dynamic game where a first player 1 without a type moves, and this is followed by the move of a second player 2 that is instead Bayesian. This is sometimes called a screening game – it actually resembles the scenario in the Wizard of $\mathrm{Oz}$, where an individual is hidden behind a curtain, and its actual character is unknown: is he a real wizard or just an impostor? Notably, a classic scenario where to apply this framework is the entry game, in which 1 also has an early termination option for the game. This somehow reduces the number of strategies and generally makes the problem more tractable – one does not have to plan the strategy of the Bayesian player 2 based on the history of play, but only on the type.
经济代写|博弈论作业代写GAME THEORY代考|Perfect Bayesian equilibrium
The equilibrium concept of PBE is relevant for sequential Bayesian games, i.e., dynamic games with incomplete information, as the proper extension of the simpler concept of BNE. For the basic cases of a simultaneous-move Bayesian game, or a screening game where a Bayesian player move only at the end it is actually enough to consider the BNE or the SPE (as reinterpreted in the type-agent representation), respectively. However, the PBE is not just a generalization of the BNE in the same way as the Nash equilibrium in mixed strategies or the subgame-perfect equilibrium expand the basic idea of NE. Already the latter generalization mentioned was kinda imperfect as the definition is intrinsically different: all SPEs are NEs but not the other way around, so it is not simply an adaptation of an existing concept, but rather its expansion: think of a child class in object-oriented programming, which satisfies all the properties of the parent class plus some additional ones.
For the concept of PBE, this is pushed further in that two components are required: strategies and beliefs. To check whether the concept is understood, that is, when asked for a PBE, the answer cannot just be a strategy set, but also a set of beliefs must be specified. In a sense, this additional element was not needed for games with complete information since the idea of NE is that players have beliefs, according to which they choose a best response; and, importantly, these beliefs turn out to be correct, so that the players are actually playing a best response to the strategies of each other. In this, beliefs are already implicit in the strategy played. When incomplete information comes into play, one can no longer guarantee that the beliefs are necessarily correct and adhering to reality (this will be evident in the exercises), so they must be explicitly specified. Still, the beliefs cannot be fully detached from the strategies, as we require some degree of internal consistency, provided by sequential rationality (that must hold) and Bayes’ rule to update them, from which this class of games takes its name.
In a dynamic Bayesian game, players specify their strategies so that an action is chosen per each information set, which in turn depends on the history of the gameplay. This is analogous to regular dynamic games, with the only difference that now information sets are also created based on Nature’s choice of the types, which is the first move in the dynamic setup. So, per each information set, in addition to specifying a strategic choice of action, the PBE must also indicate the belief of the player concerning what node is actually the real one within that information set. Typically, this is represented through a probability distribution over the nodes belonging to that information set, which often mirrors the type of another player that is Bayesian. Think for example of the aforementioned case of a signaling game: player 2, who is not Bayesian, just observes the signal sent by 1 but this corresponds to an information set with multiple nodes. In fact, 2 may believe that 1 is of certain type and has chosen to reach that information set because 1 is of a certain type and his/her strategy dictates to play that action when being of that type, and this has multiple possible explanations (one per type of 1). In the extensive form, this corresponds to the different nodes belonging to the same information set of which only one is the actual location of the game history: while 1 knows this, 2 does not and is undecided.
博弈论代写
经济代写|博弈论作业代写GAME THEORY代考|CHARACTERISTICS
在这类游戏中,一些或所有玩家都与一组类型相关联。类型的概念用于表示一个玩家可能拥有的关于其他玩家的信息的不完整性。一般的假设是玩家知道自己的类型,但可能只估计其他玩家的类型。实际上,这种不确定性可能只涉及部分玩家;可以拥有其他人不知道的不同类型的玩家被称为“贝叶斯”,就像游戏本身一样。虽然类型可用于区分游戏玩法的任何方面一世nCl在d一世nG吨H和在一种是b是在H一世CH一种d是n一种米一世CG一种米和在nF这lds,它们最常用于描述玩家可能的收益函数。一位这样的玩家 P 可以使用不同的收益函数在一种(⋅),在乙(⋅),在C(⋅),…代表他对可能结果的不同偏好顺序,其类型表示为一种,乙,C, 等等。反过来,这实际上意味着其他玩家不确定玩家更喜欢哪些替代方案磷,如果确切的类型磷只有 P 知道。
通常,将类型分配给玩家表示为由虚拟非理性玩家 Nature 盲目做出的决定,Nature 将它们选择为遵循概率分布的随机变量。原则上,我们应该考虑所有类型的联合分布,记为p(吨1,吨2,…,吨ñ)对于所有玩家1,2,…,ñ, 在哪里吨Ĵ是播放器的类型Ĵ. 然而,我们经常假设每个玩家的类型都是独立绘制的,因此我们可以只使用边际分布p1(吨1),p2(吨2),…,pñ(吨ñ)对于玩家 1 ,2,…,ñ,分别在哪里
p(吨1,吨2,…,吨ñ)=p1(吨1)⋅p2(吨2)⋯⋯pñ(吨ñ).
虽然从一般的角度来看,在非常特殊的情况下,假设类型之间存在某种相关性可能是有意义的,因此否定了类型的独立性,但实际上,独立性通常是出于易于处理的原因,也是为了现实主义,因为整个游戏只有两个玩家一种ndp这ss一世bl是这nl是这n和在一世吨H一种吨是p和. 因此,在绘制了类型之后,自然也揭示了类型吨Ĵ顶层Ĵ只要。
经济代写|博弈论作业代写GAME THEORY代考|RELEVANT CASES
贝叶斯博弈的一般框架可以指定到许多不同的上下文。特别是,用于每种情况的解决方案概念可能会发生变化。将纳什均衡直接扩展到贝叶斯情况称为贝叶斯纳什均衡乙ñ和它只是贝叶斯游戏的标准 NE在H一世CH,一种CC这rd一世nG吨这吨H和pr和在一世这在sd一世sC在ss一世这n,C一种nb和pr这米p吨l是吨r一种nsl一种吨和d一世n吨这一种d是n一种米一世CG一种米和. 然而,与动态游戏类似,这样的概念往往不足以以可信的方式捕捉玩家的理性行为并获得令人满意的预测。
如果该博弈只是暗示了自然选择所有参与者类型的初步行动,然后所有参与者的选择同时发生,我们可以将其视为静态贝叶斯博弈。实际上,这个名字有点误导,因为它不是一个真正的静态游戏吨H和r和一世s一种pl一种是和r,一世.和.,ñ一种吨在r和,米这在一世nGpr一世这r吨这吨H和这吨H和rs. 然而,它只是完全信息静态博弈的直接扩展,并且由于类型代理表示允许消除信息的不完整性,因此 BNE 足以表示这种情况。
如果游戏是动态的一种ndn这吨j在s吨b和C一种在s和这Fñ一种吨在r和′spr和l一世米一世n一种r是米这在和,那么解决方案的概念变得更加复杂,并且玩家可用的策略也可能会爆炸,因为它们共同考虑了多种类型和不同回合的游戏玩法。通常,手动调查只有 2 个玩家的场景是容易处理的,其中只有一个是贝叶斯,并且只允许两轮交互。
这导致了以下相关案例,对于这些案例,解决方法有些标准化。第一种是动态博弈的情况,其中没有类型的第一个玩家 1 移动,随后是贝叶斯的第二个玩家 2 的移动。这有时被称为筛选游戏 – 它实际上类似于巫师中的场景这和,其中一个人隐藏在窗帘后面,其实际性格未知:他是真正的巫师还是冒名顶替者?值得注意的是,应用此框架的经典场景是入门游戏,其中 1 还具有游戏的提前终止选项。这在某种程度上减少了策略的数量,并且通常使问题更容易处理——不必根据游戏历史来计划贝叶斯玩家 2 的策略,而只需根据类型。
经济代写|博弈论作业代写GAME THEORY代考|PERFECT BAYESIAN EQUILIBRIUM
PBE 的均衡概念与序列贝叶斯博弈有关,即信息不完全的动态博弈,是 BNE 更简单概念的适当扩展。对于同时移动的贝叶斯博弈的基本情况,或者贝叶斯玩家只在最后移动的筛选博弈,实际上考虑 BNE 或 SPE 就足够了一种sr和一世n吨和rpr和吨和d一世n吨H和吨是p和−一种G和n吨r和pr和s和n吨一种吨一世这n, 分别。然而,PBE 不仅仅是 BNE 的推广,就像混合策略中的纳什均衡或子博弈完美均衡扩展了 NE 的基本思想一样。提到的后一种概括已经有点不完美,因为定义本质上是不同的:所有 SPE 都是 NE,但不是相反,所以它不仅仅是对现有概念的改编,而是它的扩展:想想对象中的子类面向编程,它满足父类的所有属性以及一些附加属性。
对于 PBE 的概念,这被进一步推动,因为它需要两个组成部分:策略和信念。要检查概念是否被理解,即当被要求进行 PBE 时,答案不能只是一个策略集,还必须指定一组信念。从某种意义上说,对于具有完整信息的游戏来说,这个额外的元素是不需要的,因为 NE 的想法是玩家有信念,他们会根据信念选择最佳响应;而且,重要的是,这些信念被证明是正确的,因此玩家实际上是在对彼此的策略做出最佳反应。在这一点上,信念已经隐含在所玩的策略中。当不完整的信息发挥作用时,人们无法再保证信念一定是正确的并符合现实吨H一世s在一世llb和和在一世d和n吨一世n吨H和和X和rC一世s和s,因此必须明确指定它们。尽管如此,信念不能完全脱离策略,因为我们需要某种程度的内部一致性,由顺序理性提供吨H一种吨米在s吨H这ld以及更新它们的贝叶斯规则,此类游戏的名称就是由此而来。
在动态贝叶斯博弈中,玩家指定他们的策略,以便根据每个信息集选择一个动作,这又取决于游戏的历史。这类似于常规的动态游戏,唯一的区别是现在信息集也是根据自然对类型的选择创建的,这是动态设置中的第一步。因此,对于每个信息集,除了指定行动的战略选择外,PBE 还必须表明玩家对该信息集中哪个节点实际上是真实节点的信念。通常,这通过属于该信息集的节点上的概率分布来表示,这通常反映了另一个玩家的类型,即贝叶斯。以前面提到的信号游戏为例:不是贝叶斯的玩家 2,只观察 1 发送的信号,但这对应于具有多个节点的信息集。事实上,2 可能认为 1 属于某种类型并选择到达该信息集,因为 1 属于某种类型并且他/她的策略要求在属于该类型时执行该动作,这有多种可能的解释这n和p和r吨是p和这F1. 在扩展形式中,这对应于属于同一信息集的不同节点,其中只有一个是游戏历史的实际位置:虽然 1 知道这一点,但 2 不知道并且尚未确定。

经济代写|博弈论作业代写game theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。