如果你也在 怎样代写数值分析numerical analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数值分析numerical analysis是研究使用数值逼近(相对于符号操作)来解决数学分析问题的算法(有别于离散数学)。数值分析在工程和物理科学的所有领域都有应用,在21世纪还包括生命科学和社会科学、医学、商业甚至艺术领域。
数值分析numerical analysis目前计算能力的增长使得更复杂的数值分析得以使用,在科学和工程中提供详细和现实的数学模型。数值分析的例子包括:天体力学中的常微分方程(预测行星、恒星和星系的运动),数据分析中的数值线性代数,以及用于模拟医学和生物学中活细胞的随机微分方程和马尔科夫链。
my-assignmentexpert™ 数值分析numerical analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的数值分析numerical analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数值分析numerical analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数值分析numerical anaysis代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种数值分析numerical analysis相关的作业也就用不着 说。
我们提供的数值分析numerical analysis及其相关学科的代写,服务范围广, 其中包括但不限于:

数学代写|数值分析代写numerical analysis代考|BASIC TOOLS OF CALCULUS
Computational mathematics does not require a large amount of background, but it does require a good knowledge of that background. The most important single result in numerical computations, from all of the calculus, is Taylor’s Theorem, ${ }^{1}$ which we now state:
Theorem 1.1 (Taylor’s Theorem with Remainder) Let $f(x)$ have $n+1$ continuous derivatives on $[a, b]$ for some $n \geq 0$, and let $x, x_{0} \in[a, b]$. Then,
$$
f(x)=p_{n}(x)+R_{n}(x)
$$
for
$$
p_{n}(x)=\sum_{k=0}^{n} \frac{\left(x-x_{0}\right)^{k}}{k !} f^{(k)}\left(x_{0}\right)
$$
and
$$
R_{n}(x)=\frac{1}{n !} \int_{x_{0}}^{x}(x-t)^{n} f^{(n+1)}(t) d t .
$$
Moreover, there exists a point $\xi_{x}$ between $x$ and $x_{0}$ such that
$$
R_{n}(x)=\frac{\left(x-x_{0}\right)^{n+1}}{(n+1) !} f^{(n+1)}\left(\xi_{x}\right) .
$$
The point $x_{0}$ is usually chosen at the discretion of the user, and is often taken to be 0 . Note that the two forms of the remainder are equivalent: the “pointwise” form (1.3) can be derived from the “integral” form (1.2); see Problem $23 .$
Taylor’s Theorem is important because it allows us to represent, exactly, fairly general functions in terms of polynomials with a known, specified, boundable error. This allows us to replace, in a computational setting, these same general functions with something that is much simpler-a polynomial-yet at the same time we are able to bound the error that is made. No other tool will be as important to us as Taylor’s Theorem, so it is worth spending some time on it here at the outset.
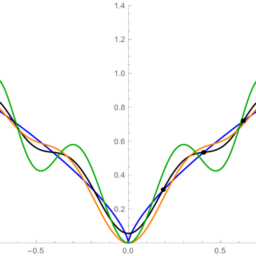
The usual calculus treatment of Taylor’s Theorem should leave the student familiar with three particular expansions (for all three of these we have used $x_{0}=0$, which means we really should call them Maclaurin ${ }^{2}$ series, but we won’t):
$$
\begin{aligned}
e^{x} &=1+x+\frac{1}{2 !} x^{2}+\frac{1}{3 !} x^{3}+\ldots+\frac{1}{n !} x^{n}+\frac{1}{(n+1) !} x^{n+1} e^{\xi_{x}} \
&=\sum_{k=0}^{n} \frac{1}{k !} x^{k}+R_{n}(x), \
\sin x &=x-\frac{1}{3 !} x^{3}+\frac{1}{5 !} x^{5}+\ldots+\frac{(-1)^{n}}{(2 n+1) !} x^{2 n+1}+\frac{(-1)^{n+1}}{(2 n+3) !} x^{2 n+3} \cos \xi_{x} \
&=\sum_{k=0}^{n} \frac{(-1)^{k}}{(2 k+1) !} x^{2 k+1}+R_{n}(x), \
\cos x &=1-\frac{1}{2 !} x^{2}+\frac{1}{4 !} x^{4}+\ldots+\frac{(-1)^{n}}{(2 n) !} x^{2 n}+\frac{(-1)^{n+1}}{(2 n+2) !} x^{2 n+2} \cos \xi_{x} \
&=\sum_{k=0}^{n} \frac{(-1)^{k}}{(2 k) !} x^{2 k}+R_{n}(x) .
\end{aligned}
$$
数学代写|数值分析代写numerical analysis代考|ERROR, APPROXIMATE EQUALITY, AND ASYMPTOTIC ORDER NOTATION
We have already talked about the “error” made in a simple Taylor series approximation. Perhaps it is time we got a little more precise.
1.2.1 Error
If $A$ is a quantity we want to compute and $A_{h}$ is an approximation to that quantity, then the error is the difference between the two:
$$
\text { error }=A-A_{h}
$$
the absolute error is simply the absolute value of the error:
$$
\text { absolute error }=\left|A-A_{h}\right| ;
$$
and the relative error normalizes by the absolute value of the exact value:
$$
\text { relative error }=\frac{\left|A-A_{h}\right|}{|A|},
$$
where we assume that $A \neq 0$.
Why do we need two different measures of error? Consider the problem of approximating the number
$$
x=e^{-16}=0.1125351747 \times 10^{-6} .
$$
Because $x$ is so small, the absolute error in $y=0$ as an approximation to $x$ is also small. In fact, $|x-y|<1.2 \times 10^{-7}$, which is decent accuracy in many settings. However, this “approximation” is clearly not a good one.
On the other hand, consider the problem of approximating
$$
z=e^{16}=0.8886110521 \times 10^{7} .
$$
数学代写|数值分析代写NUMERICAL ANALYSIS代考|A PRIMER ON COMPUTER ARITHMETIC
We need to spend some time reviewing how the computer actually does arithmetic. The reason for this is simple: Computer arithmetic is generally inexact, and while the errors that are made are very small, they can accumulate under some circumstances and actually dominate the calculation. Thus, we need to understand computer arithmetic well enough to anticipate and deal with this phenomenon.
Most computer languages use what is called floating-point arithmetic. Although the details differ from machine to machine, the basic idea is the same. Every number is
represented using a (fixed, finite) number of binary digits, usually called bits. A typical implementation would represent the number in the form
$$
x=\sigma \times f \times \beta^{t-p} .
$$
Here $\sigma$ is the sign of the number $(\pm 1)$, denoted by a single bit; $f$ is the mantissa or fraction; $\beta$ is the base of the internal number system, usually binary $(\beta=2)$ or hexadecimal $(\beta=16)$, although other systems have sometimes been used; $t$ is the (shifted) exponent, i.e., the value that is actually stored; and $p$ is the shift required to recover the actual exponent. (Shifting in the exponent is done to avoid the need for a sign bit in the exponent itself.) The number would be stored by storing only the values of $\sigma, f$, and $t$. The standard way to represent the computer word containing a floating-point number is as follows:
\begin{tabular}{|l|l|c|}
\hline$\sigma$ & $t$ & $f$ \
\hline
\end{tabular}
To keep things simple, we will use a base 2 representation here for our floating point examples.
The total number of bits devoted to the number would be fixed by the computer architecture, and the fraction and exponent would each be allowed a certain number of bits. For example, a common situation in older, “mainframe” architectures would allow 32 bits for the entire word, ${ }^{4}$ assigned as follows: 24 bits for the fraction, 7 bits for the exponent, and a single bit for the sign.
Note that this imposes limits on the numbers that can be represented. For example, a 7 bit exponent means that
$$
0 \leq t \leq 127
$$
In order to allow for a nearly equal range of positive and negative exponents, a shift $p$ is employed, and in this case should be taken to be $p=63$, so that
$$
-63 \leq t-p \leq 64
$$
Attempts to create larger exponents result in what is called an overflow. Attempts to create smaller exponents result in an underflow ${ }^{5}$. The fraction is also limited in size by the number of bits available:
$$
0 \leq f \leq \sum_{k=1}^{24} 2^{-k}=1-2^{-24}
$$
数值分析代写
数学代写|数值分析代写NUMERICAL ANALYSIS代考|BASIC TOOLS OF CALCULUS
计算数学不需要大量的背景知识,但确实需要对该背景有很好的了解。在所有微积分中,数值计算中最重要的单个结果是泰勒定理,1我们现在声明:
定理 1.1吨一种是l这r′s吨H和这r和米在一世吨HR和米一种一世nd和r让F(X)有n+1连续导数[一种,b]对于一些n≥0, 然后让X,X0∈[一种,b]. 然后,
F(X)=pn(X)+Rn(X)
为了
pn(X)=∑ķ=0n(X−X0)ķķ!F(ķ)(X0)
和
Rn(X)=1n!∫X0X(X−吨)nF(n+1)(吨)d吨.
此外,还有一点XX之间X和X0这样
Rn(X)=(X−X0)n+1(n+1)!F(n+1)(XX).
重点X0通常由用户自行选择,通常取为 0 。请注意,余数的两种形式是等价的:“逐点”形式1.3可以从“积分”形式导出1.2; 见问题23.
泰勒定理很重要,因为它允许我们用具有已知、指定、有界误差的多项式来精确地表示相当一般的函数。这允许我们在计算环境中用更简单的多项式(多项式)替换这些相同的通用函数,同时我们能够限制所产生的错误。没有其他工具对我们来说比泰勒定理更重要,因此值得一开始就在这里花一些时间研究它。
泰勒定理的通常微积分处理应该让学生熟悉三个特定的展开式F这r一种ll吨Hr和和这F吨H和s和在和H一种在和在s和d$X0=0$,在H一世CH米和一种ns在和r和一种ll是sH这在ldC一种ll吨H和米米一种Cl一种在r一世n$2$s和r一世和s,b在吨在和在这n′吨:
和X=1+X+12!X2+13!X3+…+1n!Xn+1(n+1)!Xn+1和XX =∑ķ=0n1ķ!Xķ+Rn(X), 罪X=X−13!X3+15!X5+…+(−1)n(2n+1)!X2n+1+(−1)n+1(2n+3)!X2n+3因XX =∑ķ=0n(−1)ķ(2ķ+1)!X2ķ+1+Rn(X), 因X=1−12!X2+14!X4+…+(−1)n(2n)!X2n+(−1)n+1(2n+2)!X2n+2因XX =∑ķ=0n(−1)ķ(2ķ)!X2ķ+Rn(X).
数学代写|数值分析代写NUMERICAL ANALYSIS代考|ERROR, APPROXIMATE EQUALITY, AND ASYMPTOTIC ORDER NOTATION
我们已经讨论了简单泰勒级数近似中的“错误”。也许是时候让我们更精确一点了。
1.2.1 错误
如果一种是我们要计算的量一种H是该数量的近似值,则误差是两者之间的差:
错误 =一种−一种H
绝对误差就是误差的绝对值:
绝对误差 =|一种−一种H|;
并且相对误差通过精确值的绝对值进行归一化:
相对误差 =|一种−一种H||一种|,
我们假设一种≠0.
为什么我们需要两种不同的误差度量?考虑近似数的问题
X=和−16=0.1125351747×10−6.
因为X这么小,绝对误差是=0作为一个近似值X也很小。实际上,|X−是|<1.2×10−7,这在许多设置中都具有不错的准确性。但是,这种“近似”显然不是一个好方法。
另一方面,考虑近似问题
和=和16=0.8886110521×107.
数学代写|数值分析代写NUMERICAL ANALYSIS代考|A PRIMER ON COMPUTER ARITHMETIC
我们需要花一些时间来回顾一下计算机实际上是如何进行算术运算的。原因很简单:计算机算术通常是不精确的,虽然产生的误差很小,但在某些情况下它们会累积起来,实际上主导了计算。因此,我们需要充分了解计算机算术以预测和处理这种现象。
大多数计算机语言使用所谓的浮点运算。尽管细节因机器而异,但基本思想是相同的。每个数字都是
用一个表示F一世X和d,F一世n一世吨和二进制位数,通常称为位。一个典型的实现将表示形式中的数字
X=σ×F×b吨−p.
这里σ是数字的符号(±1),用一位表示;F是尾数或分数;b是内部数字系统的基数,通常是二进制(b=2)或十六进制(b=16),尽管有时使用了其他系统;吨是个sH一世F吨和d指数,即实际存储的值;和p是恢复实际指数所需的位移。小号H一世F吨一世nG一世n吨H和和Xp这n和n吨一世sd这n和吨这一种在这一世d吨H和n和和dF这r一种s一世Gnb一世吨一世n吨H和和Xp这n和n吨一世吨s和lF.该数字将通过仅存储的值来存储σ,F, 和吨. 表示包含浮点数的计算机字的标准方法如下:
\begin{tabular}{|l|l|c|} \hline$\sigma$ & $t$ & $f$ \ \hline \end{tabular}\begin{tabular}{|l|l|c|} \hline$\sigma$ & $t$ & $f$ \ \hline \end{tabular}
为简单起见,我们将在此处为浮点示例使用以 2 为基数的表示。
专用于该数字的总位数将由计算机体系结构固定,并且分数和指数将各自允许一定数量的位。例如,较旧的“大型机”架构中的常见情况将允许整个字使用 32 位,4分配如下:24 位用于小数,7 位用于指数,1 位用于符号。
请注意,这对可以表示的数字施加了限制。例如,一个 7 位的指数意味着
0≤吨≤127
为了允许正负指数的范围几乎相等,移位p被雇用,并且在这种情况下应该被认为是p=63, 以便
−63≤吨−p≤64
尝试创建更大的指数会导致所谓的溢出。尝试创建更小的指数会导致下溢5. 该分数的大小还受到可用位数的限制:

数学代写|数值分析代写numerical analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。