如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。有限元方法finite differences method在数值分析中,是一类通过用有限差分逼近导数解决微分方程的数值技术。空间域和时间间隔(如果适用)都被离散化,或被分成有限的步骤,通过解决包含有限差分和附近点的数值的代数方程来逼近这些离散点的解的数值。
有限元方法finite differences method有限差分法将可能是非线性的常微分方程(ODE)或偏微分方程(PDE)转换成可以用矩阵代数技术解决的线性方程系统。现代计算机可以有效地进行这些线性代数计算,再加上其相对容易实现,使得FDM在现代数值分析中得到了广泛的应用。今天,FDM与有限元方法一样,是数值解决PDE的最常用方法之一。
my-assignmentexpert™ 有限元方法finite differences method作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的有限元方法finite differences method作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此有限元方法finite differences method作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的有限元方法finite differences method代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种有限元方法finite differences method相关的作业也就用不着 说。
我们提供的有限元方法finite differences method及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
数学代写|有限元方法作业代写finite differences method代考|Classification of differential operators
The quantities of interest in many areas of applied mathematics are often to be found as the solution of certain partial differential equations, together with prescribed boundary and/or initial conditions.
The nature of the solution of a partial differential equation depends on the form that the equation takes. All linear, and quasi-linear, second-order equations are classified as elliptic, hyperbolic or parabolic. In each of these categories there are equations which model certain physical phenomena. The classification is determined by the coefficients of the highest partial derivatives which occur in the equation.
In this chapter, we shall consider functions which depend on two independent variables only, so that the resulting algebra does not obscure the underlying ideas.
Consider the second-order partial differential equation
$$
\mathcal{L} u=f
$$
where $\mathcal{L}$ is the operator defined by
$$
\mathcal{L} u \equiv a \frac{\partial^{2} u}{\partial x^{2}}+b \frac{\partial^{2} u}{\partial x \partial y}+c \frac{\partial^{2} u}{\partial^{2} y^{2}}+F\left(x, y, u, \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}\right)
$$
数学代写|有限元方法作业代写finite differences method代考|Self-adjoint positive definite operators
Suppose that the function $u$ satisfies eqn (2.1) in a two-dimensional region $D$ bounded by a closed curve $C$, i.e.
$$
\mathcal{L} u=f
$$
where $f(x, y)$ is a given function of position. Suppose also that $u$ satisfies certain given homogeneous conditions on the boundary $C$. Usually these conditions are of the following types:
Dirichlet boundary condition: $u=0$;
$$
\text { Neumann condition: } \frac{\partial u}{\partial n}=0 \text {; }
$$
Robin condition: $\frac{\partial u}{\partial n}+\sigma(s) u=0$.
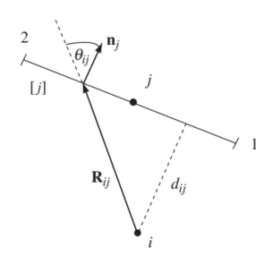
Here $s$ is the arc length measured along $C$ from some fixed point on $C$, and $\partial / \partial n$ represents differentiation along the outward normal to the boundary. Note that the Neumann condition may be obtained from the Robin condition by setting $\sigma \equiv 0$.
A problem is said to be properly posed, in the sense of Hadamard (1923), if and only if the following conditions hold:
- A solution exists.
- The solution is unique.
3 . The solution depends continuously on the data.
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|Weighted residual methods
Consider the boundary-value problem
$$
\mathcal{L} u=f \quad \text { in } \quad D
$$
subject to the non-homogeneous Dirichlet boundary condition
$$
u=g(s)
$$
on some part $C_{1}$ of the boundary, and the non-homogeneous Robin condition
$$
\frac{\partial u}{\partial n}+\sigma(s) u=h(s)
$$
on the remainder $C_{2}$.
An approximate solution $\tilde{u}$ will not, in general, satisfy eqn (2.6) exactly, and associated with such an approximate solution is the residual defined by
$$
r(\tilde{u})=\mathcal{L} \tilde{u}-f
$$
If the exact solution is $u_{0}$, then
$$
r\left(u_{0}\right) \equiv 0 .
$$
有限元方法代写
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|CLASSIFICATION OF DIFFERENTIAL OPERATORS
应用数学的许多领域中感兴趣的量通常可以作为某些偏微分方程的解以及规定的边界和/或初始条件来找到。
偏微分方程解的性质取决于方程所采用的形式。所有线性和准线性二阶方程都分类为椭圆、双曲线或抛物线。在这些类别中的每一个中,都有对某些物理现象进行建模的方程。分类由方程中出现的最高偏导数的系数确定。
在本章中,我们将考虑仅依赖于两个自变量的函数,这样所得到的代数就不会模糊其基本思想。
考虑二阶偏微分方程
大号在=F
在哪里大号是由定义的运算符
大号在≡一种∂2在∂X2+b∂2在∂X∂是+C∂2在∂2是2+F(X,是,在,∂在∂X,∂在∂是)
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|SELF-ADJOINT POSITIVE DEFINITE OPERATORS
假设函数在满足 eqn2.1在二维区域D以闭合曲线为界C, IE
大号在=F
在哪里F(X,是)是位置的给定函数。还假设在满足边界上某些给定的均匀条件C. 通常这些条件有以下几种类型:
Dirichlet 边界条件:在=0;
诺依曼条件: ∂在∂n=0;
罗宾条件:∂在∂n+σ(s)在=0.
这里s是沿测量的弧长C从某个固定点开始C, 和∂/∂n表示沿边界外法线的微分。请注意,可以通过设置从 Robin 条件获得 Neumann 条件σ≡0.
在 Hadamard 的意义上,一个问题被认为是恰当地提出的1923,当且仅当以下条件成立:
- 存在解决方案。
- 解决方案是独一无二的。
3. 解决方案持续依赖于数据。
数学代写|有限元方法作业代写FINITE DIFFERENCES METHOD代考|WEIGHTED RESIDUAL METHODS
考虑边值问题
大号在=F 在 D
服从非齐次狄利克雷边界条件
在=G(s)
在某些方面C1边界和非齐次 Robin 条件
∂在∂n+σ(s)在=H(s)
剩下的C2.
近似解在~一般不会满足 eqn2.6确切地说,与这种近似解相关联的是由下式定义的残差
r(在~)=大号在~−F
如果确切的解决方案是在0, 然后
r(在0)≡0.

数学代写|有限元方法作业代写finite differences method代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。