如果你也在 怎样代写复杂网络complex networks这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。复杂网络complex networks在网络理论的背景下,是一种具有非微观拓扑特征的图(网络)–这些特征在简单的网络(如格子或随机图)中不会出现,但在代表真实系统的网络中经常出现。复杂网络的研究是一个年轻而活跃的科学研究领域(自2000年以来),主要受到现实世界网络的经验发现的启发,如计算机网络、生物网络、技术网络、大脑网络、气候网络和社会网络。
复杂网络complex networks有两类众所周知且研究较多的复杂网络是无标度网络和小世界网络,它们的发现和定义是该领域的典型案例研究。两者都具有特定的结构特征–前者是幂律学位分布,后者是短路径长度和高聚类。然而,随着复杂网络研究的重要性和受欢迎程度不断提高,网络结构的许多其他方面也引起了人们的注意。
my-assignmentexpert™ 复杂网络complex networks作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的复杂网络complex networks作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复杂网络complex networks作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的复杂网络complex networks代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种复杂网络complex networks相关的作业也就用不着 说。
我们提供的复杂网络complex networks及其相关学科的代写,服务范围广, 其中包括但不限于:
非线性方法 nonlinear method functional analysis
变分法 Calculus of Variations
数学代写|复杂网络作业代写complex networks代考|Edge Betweenness and Community Detection
Freeman $[16]$ proposed a measure of centrality for the actors in a social network which he called “betweenness”. The betweenness of an actor is defined to be the number of shortest paths between pairs of vertices that pass through that actor. In cases where the number $p$ of shortest paths between a vertex pair is greater than one, each path is given an equal weight of $1 / p$. Trivial algorithms for calculating betweenness take $\mathrm{O}\left(\mathrm{mn}^{2}\right)$ time to calculate betweenness for all vertices, or $\mathrm{O}\left(n^{3}\right)$ time on a sparse graph (i.e., one in which the number of edges per vertex is constant in the limit of large graph size). This makes the calculation prohibitively costly on large networks. Recently however, two new algorithms have been proposed $[33,9]$ that both allow the same calculation to be performed faster, in time $\mathrm{O}(m n)$, or $\mathrm{O}\left(n^{2}\right)$ on a sparse graph, by eliminating needless recalculations of geodesic paths. The betweenness of a vertex gives an indication,
70 M.E.J. Newman and M. Girvan
as the name implies, of how much the vertex is “between” other vertices. If, for example, information (or anything else) spreads through a network primarily by following shortest paths, then betweenness scores will indicate through which vertices most information will flow on average. The vertices with highest betweenness are also those whose removal will result in an increase to the geodesic distance between the largest number of other vertex pairs.
Here we consider an extension of Freeman’s betweenness to the edges in a network. The betweenness of an edge is defined to be the number of shortest paths between pairs of vertices that run along that edge, with paths again being given weights $1 / p$ when there are $p>1$ between a given pair of vertices. In fact, the concept of edge betweenness actually appears to predate Freeman’s work on vertex betweenness, having appeared in an obscure technical report by an Amsterdam mathematician some years earlier [4]. Edge betweenness has received very little attention in other literature until recently, but it provides us with an excellent measure of which edges in a network lie between different communities. In a network with strong community structure – groups of vertices with only a few inter-group edges joining them – at least some of the intergroup edges will necessarily receive high edge betweenness scores, since they must carry the geodesic paths between vertex pairs that lie in different communities. This implies that eliminating edges with high edge betweenness from a graph will remove the inter-group edges, and hence split the graph efficiently into its different groups. This is the principle behind our method for the detection of community structure. Our algorithm is as follows.
- We calculate the edge betweenness of every edge in the network.
- We remove the edge with the highest betweenness score, or randomly choose one such if more than one edge ties for the honour.
3 . We recalculate betweenness scores on the resulting network and repeat from step 2 until no edges remain.
数学代写|复杂网络作业代写complex networks代考|Examples
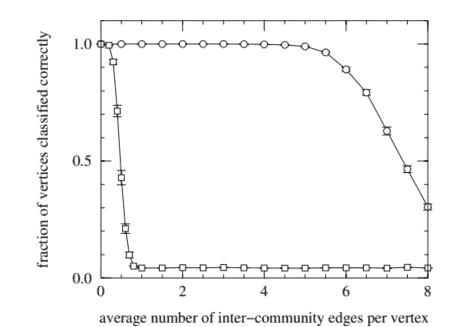
Here we give three examples of the application of our community structure finding algorithm to different networks. The first example is a set of computer generated graphs, specifically created to test the algorithm. We created a large number of graphs of 128 vertices each, divided into four groups of 32 . Edges were placed at random between vertices within the same group with probability $p_{\text {in }}$ and between vertices in different groups with probability $p_{\text {out }}$, with the values of $p_{\text {in }}$ and $p_{\text {out }}$ chosen to make the average degree of a vertex equal to 16 , and $p_{\text {out }} \leq p_{\text {in }}$. These graphs were then fed into our community structure algorithm, and we measured what fraction of the vertices were correctly classified into their communities as a function of the ratio of $p_{\text {in }}$ to $p_{\text {out }}$, or equivalently the mean number $z_{\text {out }}$ of edges from a vertex to vertices in other communities. The results are shown in Fig. 5.3. As the figure shows, the algorithm performs almost perfectly for values of $z_{\text {out }}$ up to about 6 . Beyond this point, as $z_{\text {out }}$ approaches the value of 8 at which each vertex has as many inter-group edges as intra-group ones, the fraction of successfully classified vertices falls off sharply.
On the same plot we also show the performance of a standard hierarchical clustering algorithm based on edge-independent path counts (maxflow) on the same set of random graphs. As the figure shows, the traditional method is far inferior to our new algorithm in finding the known community structure.
复杂网络代写
数学代写|复杂网络作业代写COMPLEX NETWORKS代考|EDGE BETWEENNESS AND COMMUNITY DETECTION
弗里曼[16]提出了一种衡量社会网络中参与者中心性的方法,他称之为“中介性”。一个actor的介数被定义为穿过该actor的成对顶点之间的最短路径的数量。在号码的情况下p顶点对之间的最短路径的数量大于 1,每条路径的权重相同1/p. 计算介数的简单算法这(米n2)计算所有顶点的介数的时间,或这(n3)稀疏图上的时间一世.和.,这n和一世n在H一世CH吨H和n在米b和r这F和dG和sp和r在和r吨和X一世sC这ns吨一种n吨一世n吨H和l一世米一世吨这Fl一种rG和Gr一种pHs一世和和. 这使得大型网络上的计算成本过高。然而,最近提出了两种新算法[33,9]两者都允许更快、更及时地执行相同的计算这(米n), 或者这(n2)在稀疏图上,通过消除不必要的测地线路径重新计算。一个顶点的介数表示,
70 MEJ Newman 和 M. Girvan
顾名思义,表示顶点在其他顶点之间“之间”的程度。例如,如果信息这r一种n是吨H一世nG和ls和主要通过遵循最短路径在网络中传播,然后介数分数将指示大多数信息平均将流经哪些顶点。具有最高介数的顶点也是那些其移除将导致最大数量的其他顶点对之间的测地线距离增加的顶点。
在这里,我们考虑将 Freeman 的介数扩展到网络的边缘。边的介数定义为沿该边运行的成对顶点之间的最短路径数,路径再次被赋予权重1/p当有p>1在给定的一对顶点之间。事实上,边缘介数的概念实际上似乎早于弗里曼关于顶点介数的工作,早在几年前就出现在阿姆斯特丹数学家的一份晦涩的技术报告中4. 直到最近,边缘中介性在其他文献中很少受到关注,但它为我们提供了一个很好的衡量标准,即网络中的哪些边缘位于不同的社区之间。在具有强社区结构的网络中——只有少数组间边加入的顶点组——至少一些组间边必然会获得高边介数分数,因为它们必须携带位于顶点对之间的测地线路径不同的社区。这意味着从图中消除具有高边介数的边将删除组间边,从而有效地将图拆分为不同的组。这是我们检测社区结构的方法背后的原理。我们的算法如下。
- 我们计算网络中每条边的边介数。
- 我们删除具有最高中介分数的边,或者如果有多个边与荣誉相关,则随机选择一个这样的边。
3. 我们重新计算结果网络上的中介分数,并从第 2 步开始重复,直到没有边缘存在。
数学代写|复杂网络作业代写COMPLEX NETWORKS代考|EXAMPLES
在这里,我们给出了三个将我们的社区结构查找算法应用于不同网络的示例。第一个示例是一组计算机生成的图表,专门用于测试算法。我们创建了大量的图,每个图有 128 个顶点,分为四组,每组 32 个。边以概率随机放置在同一组内的顶点之间p在 并且在不同组的顶点之间有概率p出去 ,其值为p在 和p出去 选择使顶点的平均度数等于 16 ,并且p出去 ≤p在 . 然后将这些图输入到我们的社区结构算法中,我们测量了有多少顶点被正确分类到它们的社区中,作为以下比率的函数p在 到p出去 ,或等价的平均数和出去 从一个顶点到其他社区的顶点的边数。结果如图 5.3 所示。如图所示,该算法对于和出去 最多约 6 。超过这一点,如和出去 接近 8 时,当每个顶点的组间边与组内边一样多时,成功分类的顶点的比例急剧下降。
在同一个图中,我们还展示了基于边缘无关路径计数的标准层次聚类算法的性能米一种XFl这在在同一组随机图上。如图所示,传统方法在寻找已知社区结构方面远不如我们的新算法。

数学代写|复杂网络作业代写complex networks代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。