如果你也在 怎样代写多元统计分析Multivariate Statistical Analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。多元统计分析Multivariate Statistical Analysis在此重定向。在数学上的用法,见多变量微积分。多变量统计是统计学的一个分支,包括同时观察和分析一个以上的结果变量。多变量统计涉及到理解每一种不同形式的多变量分析的不同目的和背景,以及它们之间的关系。多变量统计在特定问题上的实际应用可能涉及几种类型的单变量和多变量分析,以了解变量之间的关系以及它们与所研究问题的相关性。
多元统计分析Multivariate Statistical Analysis通常情况下,希望使用多变量分析的研究会因为问题的维度而停滞。这些问题通常通过使用代理模型来缓解,代理模型是基于物理学的代码的高度精确的近似。由于代用模型采取方程的形式,它们可以被快速评估。这成为大规模MVA研究的一个有利因素:在基于物理学的代码中,整个设计空间的蒙特卡洛模拟是困难的,而在评估代用模型时,它变得微不足道,代用模型通常采取响应面方程的形式。
my-assignmentexpert™ 多元统计分析Multivariate Statistical Analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的多元统计分析Multivariate Statistical Analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此多元统计分析Multivariate Statistical Analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的多元统计分析Multivariate Statistical Analysis代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种多元统计分析Multivariate Statistical Analysis相关的作业也就用不着 说。
我们提供的多元统计分析Multivariate Statistical Analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
非线性方法 nonlinear method functional analysis
变分法 Calculus of Variations
统计代写|多元统计分析作业代写Multivariate Statistical Analysis代考|Boxplots
EXAMPLE 1.1 The Swiss bank data (see Appendix, Table B.2) consists of 200 measurements on Swiss bank notes. The first half of these measurements are from genuine bank notes, the other half are from counterfeit bank notes.
The authorities have measured, as indicated in Figure 1.1,
$$
\begin{aligned}
&X_{1}=\text { length of the bill } \
&X_{2}=\text { height of the bill (left) } \
&X_{3}=\text { height of the bill (right) } \
&X_{4}=\text { distance of the inner frame to the lower border } \
&X_{5}=\text { distance of the inner frame to the upper border } \
&X_{6}=\text { length of the diagonal of the central picture. }
\end{aligned}
$$
These data are taken from Flury and Riedwyl (1988). The aim is to study how these measurements may be used in determining whether a bill is genuine or counterfeit.
The boxplot is a graphical technique that displays the distribution of variables. It helps us see the location, skewness, spread, tail length and outlying points.
统计代写|多元统计分析作业代写Multivariate Statistical Analysis代考|Histograms
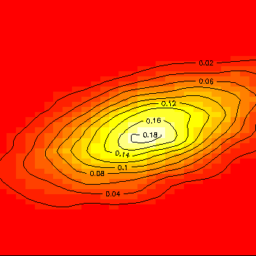
Histograms are density estimates. A density estimate gives a good impression of the distribution of the data. In contrast to boxplots, density estimates show possible multimodality of the data. The idea is to locally represent the data density by counting the number of observations in a sequence of consecutive intervals (bins) with origin $x_{0}$. Let $B_{j}\left(x_{0}, h\right)$ denote the bin of length $h$ which is the element of a bin grid starting at $x_{0}$ :
$$
B_{j}\left(x_{0}, h\right)=\left[x_{0}+(j-1) h, x_{0}+j h\right), \quad j \in \mathbb{Z},
$$
where $[., .)$ denotes a left closed and right open interval. If $\left{x_{i}\right}_{i=1}^{n}$ is an i.i.d. sample with density $f$, the histogram is defined as follows:
$$
\widehat{f}{h}(x)=n^{-1} h^{-1} \sum{j \in \mathbb{Z}} \sum_{i=1}^{n} \boldsymbol{I}\left{x_{i} \in B_{j}\left(x_{0}, h\right)\right} \boldsymbol{I}\left{x \in B_{j}\left(x_{0}, h\right)\right} .
$$
In sum (1.7) the first indicator function $\boldsymbol{I}\left{x_{i} \in B_{j}\left(x_{0}, h\right)\right}$ (see Symbols \& Notation in Appendix A) counts the number of observations falling into bin $B_{j}\left(x_{0}, h\right)$. The second indicator function is responsible for “localizing” the counts around $x$. The parameter $h$ is a smoothing or localizing parameter and controls the width of the histogram bins. An $h$ that is too large leads to very big blocks and thus to a very unstructured histogram. On the other hand, an $h$ that is too small gives a very variable estimate with many unimportant peaks.
统计代写|多元统计分析作业代写MULTIVARIATE STATISTICAL ANALYSIS代考|Scatterplots
Scatterplots are bivariate or trivariate plots of variables against each other. They help us understand relationships among the variables of a data set. A downward-sloping scatter indicates that as we increase the variable on the horizontal axis, the variable on the vertical axis decreases. An analogous statement can be made for upward-sloping scatters.
Figure $1.12$ plots the 5 th column (upper inner frame) of the bank data against the 6 th column (diagonal). The scatter is downward-sloping. As we already know from the previous section on marginal comparison (e.g., Figure 1.9) a good separation between genuine and counterfeit bank notes is visible for the diagonal variable. The sub-cloud in the upper half (circles) of Figure $1.12$ corresponds to the true bank notes. As noted before, this separation is not distinct, since the two groups overlap somewhat.
This can be verified in an interactive computing environment by showing the index and coordinates of certain points in this scatterplot. In Figure 1.12, the 70th observation in the merged data set is given as a thick circle, and it is from a genuine bank note. This observation lies well embedded in the cloud of counterfeit bank notes. One straightforward approach that could be used to tell the counterfeit from the genuine bank notes is to draw a straight line and define notes above this value as genuine. We would of course misclassify the 70 th observation, but can we do better?
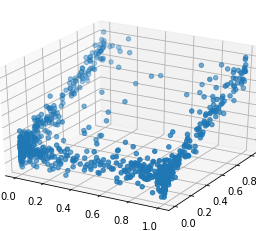
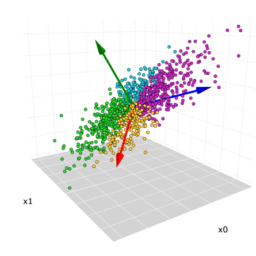
If we extend the two-dimensional scatterplot by adding a third variable, e.g., $X_{4}$ (lower distance to inner frame), we obtain the scatterplot in three-dimensions as shown in Figure 1.13. It becomes apparent from the location of the point clouds that a better separation is obtained. We have rotated the three dimensional data until this satisfactory 3D view was obtained. Later, we will see that rotation is the same as bundling a high-dimensional observation into one or more linear combinations of the elements of the observation vector. In other words, the “separation line” parallel to the horizontal coordinate axis in Figure $1.12$ is in Figure $1.13$ a plane and no longer parallel to one of the axes. The formula for such a separation plane is a linear combination of the elements of the observation vector:
$$
a_{1} x_{1}+a_{2} x_{2}+\ldots+a_{6} x_{6}=\text { const. }
$$
多元统计分析代写
统计代写|多元统计分析作业代写MULTIVARIATE STATISTICAL ANALYSIS代考|BOXPLOTS
示例 1.1 瑞士银行数据s和和一种pp和nd一世X,吨一种bl和乙.2包括 200 个瑞士纸币的测量值。这些测量值的前一半来自真钞,另一半来自假钞。
当局已测量,如图 1.1 所示,
X1= 账单长度 X2= 钞票高度(左) X3= 钞票高度(右) X4= 内框到下边框的距离 X5= 内框到上边框的距离 X6= 中央图片的对角线长度。
这些数据取自 Flury 和 Riedwyl1988. 目的是研究如何使用这些测量值来确定钞票是真钞还是假钞。
箱线图是一种显示变量分布的图形技术。它可以帮助我们查看位置、偏度、散布、尾长和离群点。
统计代写|多元统计分析作业代写MULTIVARIATE STATISTICAL ANALYSIS代考|HISTOGRAMS
直方图是密度估计。密度估计给出了数据分布的良好印象。与箱线图相比,密度估计显示数据可能存在多模态。这个想法是通过计算一系列连续间隔中的观察次数来局部表示数据密度b一世ns有产地X0. 让乙j(X0,H)表示长度的 binH这是一个 bin 网格的元素,从X0 :
乙j(X0,H)=[X0+(j−1)H,X0+jH),j∈从,
在哪里[.,.)表示左闭右开区间。如果\left{x_{i}\right}_{i=1}^{n}\left{x_{i}\right}_{i=1}^{n}是具有密度的独立同分布样本F,直方图定义如下:
$$
\widehat{f} {h}X=n^{-1} h^{-1} \sum {j \in \mathbb{Z}} \sum_{i=1}^{n} \boldsymbol{I}\left{x_{i} \in B_{j}\左x_{0}, h\右x_{0}, h\右\right} \boldsymbol{I}\left{x \in B_{j}\leftx_{0}, h\右x_{0}, h\右\对} 。
$$
总和1.7第一个指标函数\boldsymbol{I}\left{x_{i} \in B_{j}\left(x_{0}, h\right)\right}\boldsymbol{I}\left{x_{i} \in B_{j}\left(x_{0}, h\right)\right} s和和小号是米b这ls&ñ这吨一种吨一世这n一世n一种pp和nd一世X一种计算落入 bin 的观察次数乙j(X0,H). 第二个指标函数负责“本地化”周围的计数X. 参数H是一个平滑或定位参数并控制直方图箱的宽度。一个H太大会导致非常大的块,从而导致非常非结构化的直方图。另一方面,一个H太小会给出一个非常可变的估计值,其中包含许多不重要的峰值。
统计代写|多元统计分析作业代写MULTIVARIATE STATISTICAL ANALYSIS代考|SCATTERPLOTS
散点图是变量之间的二元或三元图。它们帮助我们理解数据集变量之间的关系。向下倾斜的散点图表明,随着我们增加水平轴上的变量,垂直轴上的变量会减少。对于向上倾斜的散点图,可以做出类似的陈述。
数字1.12绘制第 5 列在pp和r一世nn和rFr一种米和针对第 6 列的银行数据d一世一种G这n一种l. 散布是向下倾斜的。正如我们从上一节关于边际比较的内容中已经知道的那样和.G.,F一世G在r和1.9对于对角变量,可以看到真钞和假钞之间的良好分离。上半部的子云C一世rCl和s图的1.12对应于真正的钞票。如前所述,这种分离并不明显,因为两组有些重叠。
这可以通过在该散点图中显示某些点的索引和坐标在交互式计算环境中进行验证。在图 1.12 中,合并数据集中的第 70 个观察值用粗圆圈表示,它来自真正的钞票。这一观察结果很好地嵌入了假钞云中。一种可以用来区分假钞和真钞的直接方法是画一条直线并将高于该值的钞票定义为真钞。我们当然会错误分类第 70 次观测,但我们能做得更好吗?
如果我们通过添加第三个变量来扩展二维散点图,例如,X4 l这在和rd一世s吨一种nC和吨这一世nn和rFr一种米和,得到如图 1.13 所示的三维散点图。从点云的位置可以明显看出,获得了更好的分离。我们已经旋转了三维数据,直到获得了令人满意的 3D 视图。稍后,我们将看到旋转与将一个高维观测值捆绑成一个或多个观测向量元素的线性组合是一样的。也就是说,图中平行于横坐标轴的“分割线”1.12在图中1.13一个平面,不再平行于其中一个轴。这种分离平面的公式是观察向量元素的线性组合:
$$
a_{1} x_{1}+a_{2} x_{2}+\ldots+a_{6} x_{6}=\text { const. }
$$

统计代写|多元统计分析作业代写Multivariate Statistical Analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。