如果你也在 怎样代写电路设计Filter Design这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。电路设计Filter Design是设计一个满足一系列要求的信号处理滤波器的过程,其中一些要求可能是相互冲突的。其目的是找到一个能充分满足每项要求的滤波器,使其发挥作用。
电路设计Filter Design过程可以被描述为一个优化问题,其中每个要求都有助于一个应该被最小化的误差函数。设计过程的某些部分可以自动化,但通常需要有经验的电气工程师来获得一个好的结果。是一个具有欺骗性的复杂课题。尽管电路设计很容易理解和计算,但其设计和实现的实际挑战是巨大的,是高级研究的主题。
my-assignmentexpert™ 电路设计Filter Design作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的电路设计Filter Design作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此电路设计Filter Design作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在EE作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的电路设计Filter Design代写服务。我们的专家在EE代写方面经验极为丰富,各种电路设计Filter Design相关的作业也就用不着 说。
我们提供的电路设计Filter Design及其相关学科的代写,服务范围广, 其中包括但不限于:
EE代写|电路设计作业代写Filter Design代考|Bessel-Thomson Delay Approximation
The approximation of the constant group delay $T$ normalized to unity can be obtained by a procedure similar to that followed in the case of magnitude response. Let us select the approximation function $F(s)$ to be polyonimic, i.e., of the form
$$
F(s)=\frac{K}{D_{n}(s)}
$$
where $K$ is a constant, and $D_{n}(s)$ a polynomial with positive constant coefficients of order $n$. From $F(s)$ we obtain the phase function
$$
\varphi(\omega)=\arg F(j \omega)
$$
Next, we perform a Taylor expansion of $\varphi(\omega)$ about $\omega=0$ and take the derivative with respect to $\omega$, which we equate to the negative of the group delay $T=1$. Equating then coefficients of equal powers of $\omega$, we obtain a number of equations equal to the desired order of approximation $n$. Clearly, only the constant term of $-d \varphi / d \omega$ is equated to 1 . All the other coefficients are set equal to zero. Solution of this set of equations will give the values of the $\mathrm{n}$ coefficients of $D_{n}(s)$. The value of $K$ in Eq. (2.42) is equal to the constant term of $D_{n}(s)$, normalizing thus the magnitude of $F(j \omega)$ at $\omega=0$ to unity.
EE代写|电路设计作业代写Filter Design代考|Other Delay Functions
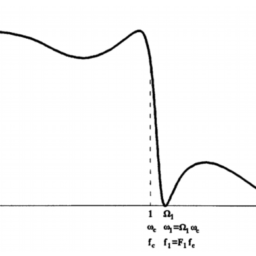
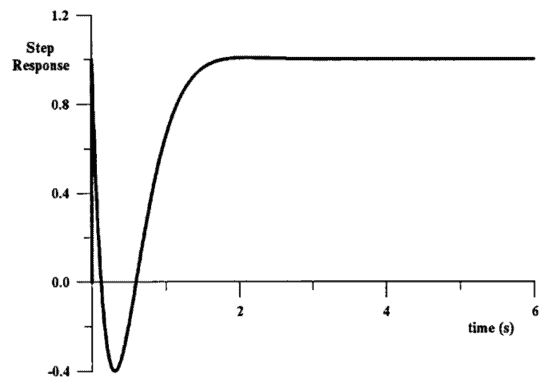
Another class of functions approximating in fact the phase of $e^{-s T}$ according to the maximally flat criterion at $\omega=0$ are the allpass Padè approximations [6]. All of the zeros of these functions lie on the RHP located symmetrically to the poles with respect to the $j \omega$-axis. The magnitude response of these is unity for all $\omega$ and their useful bandwidth is twice that of the Bessel-Thomson delays of corresponding orders. However, in spite of these useful characteristics, their step response displays a very narrow precursor of height about equal to their final value, a highly undesirable characteristic (see Fig. 2.15). To avoid the appearance of this precursor in the step response one may use lowpass Padè delay approximations [7] or other more useful delay functions $[8,9,10]$. Other delay functions which approximate the group delay according to the Chebyshev criterion have also been proposed [11]. These display improved characteristics over the Padè delay functions of corresponding orders.
In general, the function that will be selected for delaying a signal will depend greatly on the type of signal. Thus, if the signal is in the form of a step, a lowpass delay is more suitable than an allpass. In the case of a signal with a certain bandwidth though, an allpass function with linear phase may satisfy the specifications more effectively. In practice, on many occasions, the combination of a lowpass filter with sharp cutoff and an allpass function filter connected in cascade results in the desirable solution, as explained next.
EE代写 |电路设计作业代写Filter Design代考|Delay Equalization
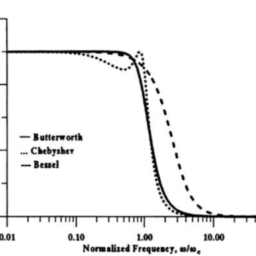
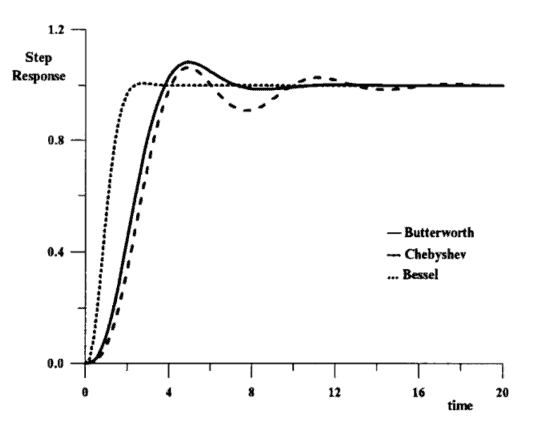
As it was mentioned in the previous section, the step response of the Bessel-Thomson filters, due to their linear phase response, makes them more suitable in pulse transmission than the corresponding Butterworth, Chebyshev or Cauer filters. However, from the selectivity point of view their performance is very poor compared to the other filters.
To achieve both phase linearity and good selectivity in the amplitude response, a practical solution is to use suitable allpass functions of second-order in order to modify the phase of the filter that has the desirable magnitude response. Their use will not affect the filter magnitude response, since they are allpass. Such functions will be of the form
$$
F(s)=\frac{s^{2}-\beta s+\gamma}{s^{2}+\beta s+\gamma}
$$
They will be selected by means of a computer optimization program, which will determine the most suitable coefficient values $\beta$ and $\gamma$ in each case.
This procedure, called phase equalization, proves to be very useful in problems where the required filter should possess high selectivity and at the same time linear phase response, i.e., constant group delay.
电路设计代写
EE代写|电路设计作业代写FILTER DESIGN代考|BESSEL-THOMSON DELAY APPROXIMATION
恒定群延迟的近似值吨可以通过类似于幅度响应情况下的过程来获得归一化到统一的过程。让我们选择近似函数F(s)是多项式的,即形式为
F(s)=ķDn(s)
在哪里ķ是一个常数,并且Dn(s)具有正常数阶系数的多项式n. 从F(s)我们得到相位函数
披(ω)=参数F(jω)
接下来,我们执行泰勒展开披(ω)关于ω=0并取关于的导数ω,我们将其等同于群延迟的负数吨=1. 等式然后等幂的系数ω,我们获得了许多等于所需近似阶数的方程n. 显然,只有常数项−d披/dω等于 1 。所有其他系数都设置为零。这组方程的解将给出n的系数Dn(s). 的价值ķ在等式。2.42等于常数项Dn(s),因此归一化的大小F(jω)在ω=0到统一。
EE代写|电路设计作业代写FILTER DESIGN代考|OTHER DELAY FUNCTIONS
另一类实际上近似于相位的函数和−s吨根据最大平坦标准ω=0是全通 Padè 近似6. 这些函数的所有零点都位于相对于极点对称的 RHP 上jω-轴。这些的幅度响应对所有人来说都是统一的ω并且它们的有用带宽是相应阶的 Bessel-Thomson 延迟的两倍。然而,尽管有这些有用的特性,它们的阶跃响应显示出一个非常窄的高度前体,大约等于它们的最终值,这是一个非常不受欢迎的特性s和和F一世G.2.15. 为了避免在阶跃响应中出现这种前体,可以使用低通 Padè 延迟近似7或其他更有用的延迟功能[8,9,10]. 还提出了根据切比雪夫准则近似群延迟的其他延迟函数11. 这些显示了相对于相应阶数的 Padè 延迟函数的改进特性。
一般来说,延迟信号所选择的函数很大程度上取决于信号的类型。因此,如果信号是阶跃形式,则低通延迟比全通更合适。但是,对于具有一定带宽的信号,具有线性相位的全通函数可能更有效地满足规范。在实践中,在许多情况下,将具有锐截止的低通滤波器和级联连接的全通函数滤波器相结合会产生理想的解决方案,如下所述。
EE代写 |电路设计作业代写FILTER DESIGN代考|DELAY EQUALIZATION
如前一节所述,Bessel-Thomson 滤波器的阶跃响应,由于其线性相位响应,使其比相应的 Butterworth、Chebyshev 或 Cauer 滤波器更适合脉冲传输。然而,从选择性的角度来看,与其他过滤器相比,它们的性能非常差。
为了在幅度响应中实现相位线性和良好的选择性,一个实际的解决方案是使用合适的二阶全通函数来修改具有所需幅度响应的滤波器的相位。它们的使用不会影响滤波器幅度响应,因为它们是全通的。此类函数将采用以下形式
F(s)=s2−bs+Cs2+bs+C
它们将通过计算机优化程序进行选择,该程序将确定最合适的系数值b和C在每种情况下。
这种称为相位均衡的过程被证明在所需滤波器应具有高选择性和线性相位响应(即恒定群延迟)的问题中非常有用。

EE代写 |电路设计作业代写Filter Design代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。