如果你也在 怎样代写电路设计Filter Design这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。电路设计Filter Design是设计一个满足一系列要求的信号处理滤波器的过程,其中一些要求可能是相互冲突的。其目的是找到一个能充分满足每项要求的滤波器,使其发挥作用。
电路设计Filter Design过程可以被描述为一个优化问题,其中每个要求都有助于一个应该被最小化的误差函数。设计过程的某些部分可以自动化,但通常需要有经验的电气工程师来获得一个好的结果。是一个具有欺骗性的复杂课题。尽管电路设计很容易理解和计算,但其设计和实现的实际挑战是巨大的,是高级研究的主题。
my-assignmentexpert™ 电路设计Filter Design作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的电路设计Filter Design作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此电路设计Filter Design作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在EE作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的电路设计Filter Design代写服务。我们的专家在EE代写方面经验极为丰富,各种电路设计Filter Design相关的作业也就用不着 说。
我们提供的电路设计Filter Design及其相关学科的代写,服务范围广, 其中包括但不限于:
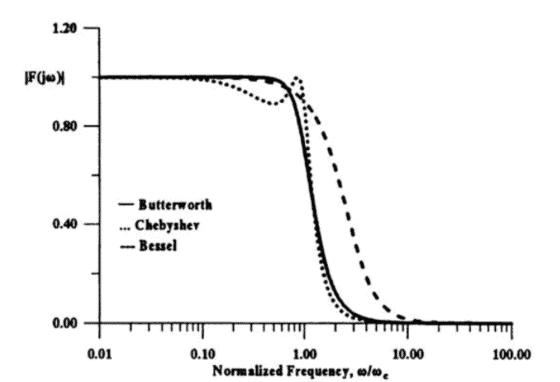
EE代写 |电路设计作业代写Filter Design代考|Butterworth or Maximally Flat Approximation
If we let $\varepsilon=1$ and
$$
w\left(\omega^{2}\right)=\omega^{2 n}
$$
in Eq. (2.5), $n$ being a positive real integer, we will get the following amplitude function:
$$
M(\omega)=\frac{1}{\left[1+\omega^{2 n}\right]^{1 / 2}}
$$
It can be seen that
$$
M(0)=1
$$
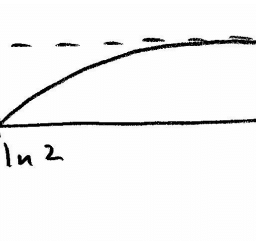
while $M(\omega)$ decreases monotonically with increasing $\omega$.
At $\omega_{c}=1$,
$$
M(1)=\frac{1}{\sqrt{2}}=0.707
$$
or
$$
20 \log M(1)=-10 \log 2=-3.01
$$
In other words, at $\omega_{c}=1$, the amplitude is $3 \mathrm{~dB}$ below its value at dc. This is the cutoff frequency of the filter. Clearly, this is independent of $n$, the order of the filter function, which in fact determines how close to the ideal is the approximating function $M(\omega)$, i.e., how successful the approximation is.
EE代写 |电路设计作业代写Filter Design代考|Chebyshev or Equiripple Approximation
In this case, Eq. (2.5) takes the following form:
$$
|F(j \omega)|^{2}=M^{2}(\omega)=\frac{1}{1+\varepsilon^{2} C_{n}^{2}(\omega)}
$$
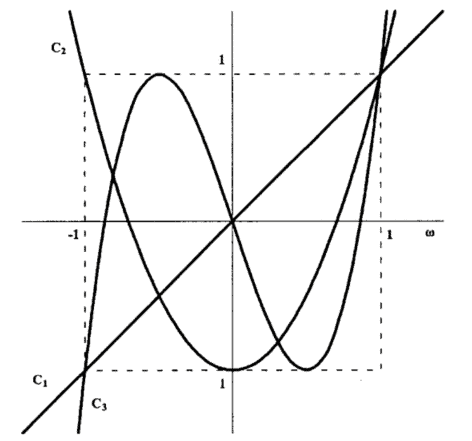
Here again, $0<\varepsilon \leq 1$, and $C_{n}(\omega)$ is a Chebyshev polynomial of degree $n$ having the following form:
$$
\begin{aligned}
C_{n}(\omega) &=\cos \left(n \cos ^{-1} \omega\right) & 0 \leq|\omega| \leq 1 \
&=\cosh \left(n \cosh ^{-1} \omega\right) & & 1 \leq|\omega|
\end{aligned}
$$
EE代写 |电路设计作业代写Filter Design代考|Inverse Chebyshev Approximation
The Chebyshev polynomials are also used to obtain the so-called Inverse Chebyshev filter functions, the magnitude of which is given as follows:
$$
M^{2}(\omega)=\frac{\varepsilon^{2} C_{n}^{2}\left(\frac{1}{\omega}\right)}{1+\varepsilon^{2} C_{n}^{2}\left(\frac{1}{\omega}\right)}
$$
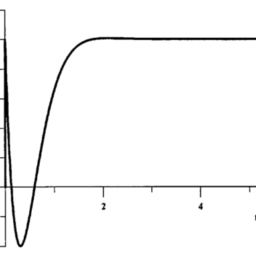
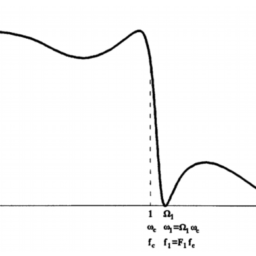
The properties of these functions are complementary to those of the Chebyshev functions in the sense that they present maximum flatness in the passband and equiripple behavior in the stopband. Also, their phase response and consequently their group delay is better than that of the Chebyshev filter. In Fig. 2.9, the magnitude response of the third-order Inverse Chebyshev and the corresponding Chebyshev function are shown for comparison.
电路设计代写
EE代写 |电路设计作业代写FILTER DESIGN代考|BUTTERWORTH OR MAXIMALLY FLAT APPROXIMATION
如果我们让e=1和
在(ω2)=ω2n
在等式。2.5, n作为一个正实整数,我们将得到以下幅度函数:
米(ω)=1[1+ω2n]1/2
可以看出
米(0)=1
尽管米(ω)随着增加单调减少ω.
在ωC=1,
米(1)=12=0.707
或者
20日志米(1)=−10日志2=−3.01
换句话说,在ωC=1,幅度为3 d乙低于其在直流值。这是滤波器的截止频率。显然,这与n,滤波器函数的阶数,实际上决定了逼近函数与理想的接近程度米(ω),即近似的成功程度。
EE代写 |电路设计作业代写FILTER DESIGN代考|CHEBYSHEV OR EQUIRIPPLE APPROXIMATION
在这种情况下,方程式。2.5采用以下形式:
|F(jω)|2=米2(ω)=11+e2Cn2(ω)
又是在这里,0<e≤1, 和Cn(ω)是次数的切比雪夫多项式n具有以下形式:
Cn(ω)=因(n因−1ω)0≤|ω|≤1 =科什(n科什−1ω)1≤|ω|
EE代写 |电路设计作业代写FILTER DESIGN代考|INVERSE CHEBYSHEV APPROXIMATION
Chebyshev 多项式也用于获得所谓的逆 Chebyshev 滤波器函数,其大小如下:
米2(ω)=e2Cn2(1ω)1+e2Cn2(1ω)
这些函数的性质与切比雪夫函数的性质互补,因为它们在通带中呈现最大平坦度,在阻带中呈现等波纹行为。此外,它们的相位响应以及因此它们的群延迟比切比雪夫滤波器更好。在图 2.9 中,显示了三阶逆切比雪夫函数和相应的切比雪夫函数的幅值响应以进行比较。

EE代写 |电路设计作业代写Filter Design代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。