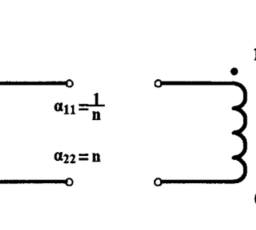
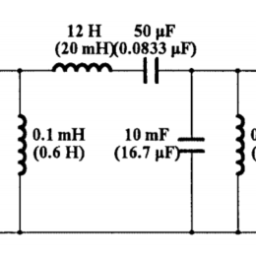
如果你也在 怎样代写电路设计Filter Design这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。电路设计Filter Design是设计一个满足一系列要求的信号处理滤波器的过程,其中一些要求可能是相互冲突的。其目的是找到一个能充分满足每项要求的滤波器,使其发挥作用。
电路设计Filter Design过程可以被描述为一个优化问题,其中每个要求都有助于一个应该被最小化的误差函数。设计过程的某些部分可以自动化,但通常需要有经验的电气工程师来获得一个好的结果。是一个具有欺骗性的复杂课题。尽管电路设计很容易理解和计算,但其设计和实现的实际挑战是巨大的,是高级研究的主题。
my-assignmentexpert™ 电路设计Filter Design作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的电路设计Filter Design作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此电路设计Filter Design作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在EE作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的电路设计Filter Design代写服务。我们的专家在EE代写方面经验极为丰富,各种电路设计Filter Design相关的作业也就用不着 说。
我们提供的电路设计Filter Design及其相关学科的代写,服务范围广, 其中包括但不限于:
EE代写 |电路设计作业代写Filter Design代考|Causality
In general, causality refers to the fact that there can be no result without cause. In the case of interest here, a causal network will not respond before an excitation has been applied to its terminals. Thus, the unit impulse response is zero for time $t<0$. The response in Fig. 2.1(a) is not causal; therefore, it cannot be realized. On the other hand, that in Fig. 2.1(b) is causal, therefore realizable. Thus, the ideal lowpass filter is unrealizable, because its impulse response is noncausal.
In the frequency domain, causality is determined by means of the Paley-Wiener criterion [1]. Consider the impulse response $h(t)$, which possesses a Fourier Transform $H(j \omega)$ for which
$$
\int_{-\infty}^{\infty}|H(j \omega)|^{2} d \omega<\infty
$$
For $H(j \omega)$ to be causal, the criterion is the following:
$$
\int_{-\infty}^{\infty} \frac{|\log | H(j \omega)||}{1+\omega^{2}} d \omega<\infty
$$
EE代写 |电路设计作业代写Filter Design代考|Rational Functions
The LLF network functions are rational, i.e., ratios of two finite polynomials of the Laplace transform variable $s$. Therefore, it is not possible to realize the function $e^{-s T}$ by such a network, because this function cannot be expressed in the form of a rational function.
EE代写 |电路设计作业代写Filter Design代考|Stability
The response of a stable network is bounded if the excitation is bounded. This means that, if $h(t)$ is the impulse response of the network, then
$$
\int_{0}^{\infty} h(t) d t<\infty
$$
and $\lim h(t) \rightarrow 0$ when $t \rightarrow \infty$.
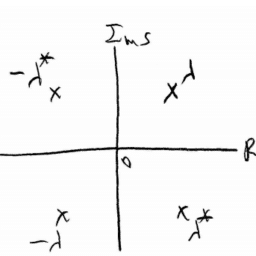
In the frequency domain, stability implies that
- the network function $H(s)$ does not have poles in the RH of the s-plane,
- any poles on the $j \omega$-axis are simple, and
- the degree of the numerator polynomial cannot be higher than the degree of the denominator by more than one.
However, for a filter to be useful, its function $H(s)$ has to be strictly stable, i.e., all its poles must be located in the LH of the $s$-plane excluding the $j \omega$-axis (poles at zero and infinity are considered to be located on the $j \omega$-axis).

电路设计代写
EE代写 |电路设计作业代写FILTER DESIGN代考|CAUSALITY
一般来说,因果关系是指没有原因就没有结果的事实。在这里感兴趣的情况下,因果网络在向其终端施加激励之前不会响应。因此,单位脉冲响应在时间上为零吨<0. 图 2.1 中的响应一种不是因果关系;因此,它无法实现。另一方面,在图 2.1b是因果的,因此是可以实现的。因此,理想的低通滤波器是无法实现的,因为它的脉冲响应是非因果的。
在频域中,因果关系通过 Paley-Wiener 准则确定1. 考虑脉冲响应H(吨), 它具有傅里叶变换H(jω)为此
∫−∞∞|H(jω)|2dω<∞
为了H(jω)作为因果关系,标准如下:
∫−∞∞|日志|H(jω)||1+ω2dω<∞
EE代写 |电路设计作业代写FILTER DESIGN代考|RATIONAL FUNCTIONS
LLF 网络函数是有理的,即拉普拉斯变换变量的两个有限多项式的比率s. 因此无法实现功能和−s吨通过这样的网络,因为这个函数不能用有理函数的形式表示。
EE代写 |电路设计作业代写FILTER DESIGN代考|STABILITY
如果激励是有界的,则稳定网络的响应是有界的。这意味着,如果H(吨)是网络的脉冲响应,那么
∫0∞H(吨)d吨<∞
和林H(吨)→0什么时候吨→∞.
在频域中,稳定性意味着
- 网络功能H(s)在 s 平面的 RH 中没有极点,
- 上的任何极jω-axis 很简单,并且
- 分子多项式的次数不能比分母的次数高一倍以上。
但是,要使过滤器有用,它的功能H(s)必须是严格稳定的,即它的所有极点都必须位于s- 平面不包括jω-轴p这l和s一种吨和和r这一种nd一世nF一世n一世吨是一种r和C这ns一世d和r和d吨这b和l这C一种吨和d这n吨H和$jω$−一种X一世s.

EE代写 |电路设计作业代写Filter Design代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。