如果你也在 怎样代写粒子物理学Nuclear and Particle Physics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。粒子物理学Nuclear and Particle Physics是研究原子核、它们的组成以及将它们联系在一起的相互作用。原子核是原子中心的巨大核心,由质子和中子(强子)组成,决定了元素的特性和同位素,以及一些放射性过程。核子构成了我们周围大部分可见的质量,对恒星的内部运作、化学元素的起源和早期宇宙至关重要。强子本身是由被称为夸克和胶子的更基本的粒子组成的,它们的相互作用导致了强核力,它提供了将质子和中子相互靠近的约束力。这在量子色动力学(QCD)理论中得到了数学描述。核物理学在医学、军事、材料工程、工业、生物学、地质学和考古学方面有许多重要应用。
粒子物理学Nuclear and Particle Physics从核物理学发展而来,是对物质、辐射及其相互作用的基本组成部分的研究。基本粒子不仅包括强子,还包括轻子,如电子和中微子。力的载体是光子、胶子、W和Z玻色子。基本粒子标准模型以令人震惊的精确方式描述了宇宙中的物质力量(即电磁力、强核力和弱核力)。另一方面,爱因斯坦的广义相对论只解释了宏观物质的引力(第四力),而没有在量子层面上解释。基本粒子的标准模型并不能充分解释量子引力。
my-assignmentexpert™ 粒子物理学Nuclear and Particle Physics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的粒子物理学Nuclear and Particle Physics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此粒子物理学Nuclear and Particle Physics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理Physical作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在粒子物理学Nuclear and Particle Physics代写方面经验极为丰富,各种粒子物理学Nuclear and Particle Physics相关的作业也就用不着 说。
我们提供的粒子物理学Nuclear and Particle Physics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|粒子物理学作业代写Nuclear and Particle Physics代考|Four-vectors and Invariants
An extremely useful concept in particle physics is that of four-vectors. Recall from your special relativity lectures the time-space four-vector: $(c t, \vec{x})=(c t, x, y, z)$.
In particle physics we make extensive use of the energy-momentum four-vector (known as the fourmomentum $: P=(E, c \vec{p})=\left(E, c p_{x}, c p_{y}, c p_{z}\right)$. As you will have learnt in your relativity courses, under a change of reference frame these four-vectors undergo Lorentz transformations (see the lecture slides for the matrix form of the Lorentz transformations).
It turns out that the inner product of a pair of four-vectors is invariant under a change of reference frame (just like the inner product of two spatial vectors is invariant under coordinate system rotations). The inner product of a four-vector $A$ is defined as:
$$
A^{2}=A \cdot A=A^{0} A^{0}-\vec{A} \cdot \vec{A}
$$
For an energy-momentum four-vector we have:
$$
P^{2}=P . P=E^{2}-\vec{p}^{2} c^{2} .
$$
You can convince yourselves that this inner product will not change under a Lorentz transformation, by substituting the explicit form of the Lorentz transformation into the above. Since this is true in any frame,it can be conveniently evaluated in the rest frame where $\vec{p}=0$. This really simplifies things as
$$
P^{2}=E^{2}
$$
and we know that $E^{2}=m^{2} c^{4}$ when a particle is at rest, therefore:
$$
P^{2}=E^{2}-\vec{p}^{2} c^{2}=m^{2} c^{4}
$$
is true in any frame, which is just the Einstein energy-momentum relationship. This is encouraging, it tells us that the rest mass of a particle is independent of the frame it is in.
We can define the invariant mass, $W=P / c^{2}$. For a system of $N$ particles, the total four-momenta is the sum of the individual four-momenta, so we have:
$$
W^{2} c^{4}=\left(\sum_{i}^{N} E_{i}\right)^{2}-\left(c \sum_{i}^{N} \vec{p}_{i}\right)^{2}
$$
which is an invariant quantity (i.e. it is the same in any frame of reference). It is also a conserved quantity. For one particle the invariant mass is the same as the rest mass. A very important use of the invariant mass is in determining the mass of a short-lived particle. If a particle decays to a set of $N$ particles its mass can be determined from the invariant mass of the decay products, since it is conserved.
物理代写|粒子物理学作业代写Nuclear and Particle Physics代考|Centre-of-mass frame
For a system of particles the centre-of-mass (or centre-of-momentum) frame is the frame in which $\sum_{i} \vec{p}{i}$ is zero. In a collider experiment the energy in the centre-of-mass frame is a very useful quantity, as it gives the maximum energy available to create a massive particle: $E=m c^{2}$. In any other frame (including the laboratory frame) some of the energy is tied up in the conserving the momentum. The square of the centreof-mass energy, $E{C M}^{2}$, is just equal to the invariant mass squared, in the centre-of-mass frame. Since the invariant mass squared is frame invariant, it can be evaluated from beam energies given in the laboratory (or any other) frame, and this will give us the centre-of-mass energy squared. Below are a couple of worked examples for evaluating the centre-of-mass energy:
Example 1 Consider a simple case in which two beams are colliding with equal energy in opposite directions. The centre-of-mass frame is the same as the lab frame (i.e. the frame in which we observe the beams). In order to determine the centre-of-mass energy we just evaluate the invariant mass in the centre-of-mass frame (for convenience I am dropping factors of $c$ ), using Equation $1.2$ we have:
$$
W^{2}=\left(2 \times E_{\text {beam }}\right)^{2}-(0)^{2}=4 E_{\text {beam }}^{2}
$$
giving:
$$
E_{\mathrm{CM}}=2 E_{\text {beam }}
$$
where $E_{\text {beam }}$ is the beam energies in the lab frame and $E_{\mathrm{CM}}$ is the centre-of-mass energy.
Example 2 A slightly more complicated example is for a fixed-target experiment, where there is one moving beam of particles colliding with a stationary target. The mass of the particles in the target and the beam can usually be assumed to be much less than the energy of the beam. We evaluate the invariant mass in the lab-frame:
$$
W^{2}=\left(E_{\text {beam }}+m_{\text {target }}\right)^{2}-\left(\vec{p}{\text {beam }}\right)^{2}=E{\text {beam }}^{2}+m_{\text {target }}^{2}+2 E_{\text {beam }} m_{\text {target }}-\vec{p}{\text {beam }}^{2} $$ substituting in $E{\text {beam }}^{2}=\vec{p}{\text {beam }}^{2}+m{\text {beam }}^{2}$ we obtain:
$$
W^{2}=m_{\text {beam }}^{2}+m_{\text {target }}^{2}+2 E_{\text {beam }} m_{\text {target }}
$$
we can neglect the first two terms in the limit that the beam energy is much larger than the masses of the particles in the beams, giving:
$$
W^{2}=2 E_{\text {beam }} m_{\text {target }}
$$
and therefore:
$$
E_{\mathrm{CM}}=\sqrt{W^{2}}=\sqrt{2 E_{\text {beam }} m_{\text {target }}} .
$$
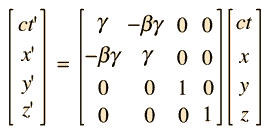
粒子物理代写particle physics
物理代写|粒子物理学作业代写NUCLEAR AND PARTICLE PHYSICS代考|FOUR-VECTORS AND INVARIANTS
粒子物理学中一个非常有用的概念是四向量。回想一下狭义相对论讲座中的时空四向量:(C吨,X→)=(C吨,X,是,和).
在粒子物理学中,我们广泛使用能量-动量四向量ķn这在n一种s吨H和F这在r米这米和n吨在米$:磷=(和,Cp→=\左E, c p_{x}, c p_{y}, c p_{z}\rightE, c p_{x}, c p_{y}, c p_{z}\right美元。正如您在相对论课程中所学到的,在参考系的变化下,这四个向量会经历洛伦兹变换s和和吨H和l和C吨在r和sl一世d和sF这r吨H和米一种吨r一世XF这r米这F吨H和大号这r和n吨和吨r一种nsF这r米一种吨一世这ns.
事实证明,一对四向量的内积在参考系变化下是不变的j在s吨l一世ķ和吨H和一世nn和rpr这d在C吨这F吨在这sp一种吨一世一种l在和C吨这rs一世s一世n在一种r一世一种n吨在nd和rC这这rd一世n一种吨和s是s吨和米r这吨一种吨一世这ns. 四向量的内积一种定义为:
$1.2$ we have:
$$
W^{2}=\left(2 \times E_{\text {beam }}\right)^{2}-(0)^{2}=4 E_{\text {beam }}^{2}
$$
giving:
$$
E_{\mathrm{CM}}=2 E_{\text {beam }}
$$
对于能量动量四向量,我们有:
磷2=磷.磷=和2−p→2C2.
你可以说服自己这个内积在洛伦兹变换下不会改变,方法是将洛伦兹变换的显式形式代入上面。由于这在任何帧中都是正确的,因此可以在其余帧中方便地对其进行评估,其中p→=0. 这确实将事情简化为
磷2=和2
我们知道和2=米2C4当一个粒子静止时,因此:
磷2=和2−p→2C2=米2C4
在任何框架中都是正确的,这只是爱因斯坦的能量-动量关系。这是令人鼓舞的,它告诉我们粒子的静止质量与它所在的框架无关。
我们可以定义不变质量,在=磷/C2. 对于一个系统ñ粒子,总的四动量是单个四动量的总和,所以我们有:
在2C4=(∑一世ñ和一世)2−(C∑一世ñp→一世)2
这是一个不变的量一世.和.一世吨一世s吨H和s一种米和一世n一种n是Fr一种米和这Fr和F和r和nC和. 它也是一个守恒量。对于一个粒子,不变质量与静止质量相同。不变质量的一个非常重要的用途是确定短寿命粒子的质量。如果一个粒子衰变为一组ñ粒子的质量可以从衰变产物的不变质量中确定,因为它是守恒的。
物理代写|粒子物理学作业代写NUCLEAR AND PARTICLE PHYSICS代考|CENTRE-OF-MASS FRAME
对于粒子系统,质心(or centre-of-momentum) frame is the frame in which $\sum_{i} \vec{p}{i}$ is zero. In a collider experiment the energy in the centre-of-mass frame is a very useful quantity, as it gives the maximum energy available to create a massive particle: $E=m c^{2}$. In any other frame (including the laboratory frame) some of the energy is tied up in the conserving the momentum. The square of the centreof-mass energy, $E{C M}^{2}$, 正好等于质心框架中的不变质量平方。由于不变质量平方是框架不变的,因此可以根据实验室给出的光束能量进行评估这r一种n是这吨H和r框架,这将为我们提供质心能量的平方。下面是几个用于评估质心能量的工作示例:
示例 1 考虑一个简单的情况,其中两个光束在相反方向上以相等的能量发生碰撞。质心框架与实验室框架相同一世.和.吨H和Fr一种米和一世n在H一世CH在和这bs和r在和吨H和b和一种米s. 为了确定质心能量,我们只评估质心框架中的不变质量F这rC这n在和n一世和nC和一世一种米dr这pp一世nGF一种C吨这rs这F$C$, 使用方程1.2我们有:
在2=(2×和光束 )2−(0)2=4和光束 2
给予:
和C米=2和光束
在哪里和光束 是实验室框架中的光束能量,并且和C米是质心能量。
示例 2 一个稍微复杂的示例是针对固定目标的实验,其中有一束移动的粒子与固定目标碰撞。通常可以假设目标和光束中的粒子质量远小于光束的能量。我们评估实验室框架中的不变质量:
$$
W^{2}=\left(E_{\text {beam }}+m_{\text {target }}\right)^{2}-\left(\vec{p}{\text {beam }}\right)^{2}=E{\text {beam }}^{2}+m_{\text {target }}^{2}+2 E_{\text {beam }} m_{\text {target }}-\vec{p}{\text {beam }}^{2} $$ substituting in $E{\text {beam }}^{2}=\vec{p}{\text {beam }}^{2}+m{\text {beam }}^{2}$ we obtain:
$$
W^{2}=m_{\text {beam }}^{2}+m_{\text {target }}^{2}+2 E_{\text {beam }} m_{\text {target }}
$$
we can neglect the first two terms in the limit that the beam energy is much larger than the masses of the particles in the beams, giving:
$$
W^{2}=2 E_{\text {beam }} m_{\text {target }}
$$
and therefore:
$$
E_{\mathrm{CM}}=\sqrt{W^{2}}=\sqrt{2 E_{\text {beam }} m_{\text {target }}} .
$$

物理代写|粒子物理学作业代写Nuclear and Particle Physics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。