如果你也在 怎样代写图论代写Graph Theory这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。图论代写Graph Theory可以用来模拟物理、生物、[社会和信息系统中的许多类型的关系和过程。许多实际问题都可以用图来表示。强调其在现实世界系统中的应用,网络一词有时被定义为一个图,其中的属性(如名称)与顶点和边相关联,而将现实世界系统作为网络来表达和理解的学科被称为网络科学。
图论代写Graph Theory在数学中,是对图的研究,它是用来模拟对象之间成对关系的数学结构。这里的图是由顶点(也叫节点或点)组成的,这些顶点由边(也叫链接或线)连接。无向图和有向图是有区别的,前者的边对称地连接两个顶点,后者的边则不对称地连接两个顶点。图是离散数学的主要研究对象之一。
my-assignmentexpert™ 图论代写Graph Theory作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的图论代写Graph Theory作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此图论代写Graph Theory作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
我们提供的图论代写Graph Theory及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|图论代写Graph Theory代考|Historical perspective
To have a connected world it is obvious that we need to communicate. If we want this world to have significant coverage, long-distance communication is obviously important. Unlike what many tend to believe, networks that facilitate such communication have a long history, as described by Holzmann and Pehrson [1995]. Apart from well-known means of communication such as sending messengers or using pigeons, long-distance communication without the need to physically transport a message has always caught the attention of mankind. Typically, such telegraphic communication used to be done through fire beacons, mirrors (i.e., heliographic communication), drums, and flags. Communication paths set up using such methods, for ex-ample by having communication posts organized at line-of-sight distances, are known from Greek and Roman history.
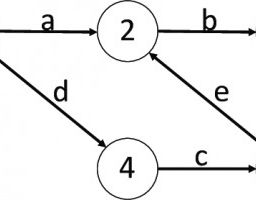
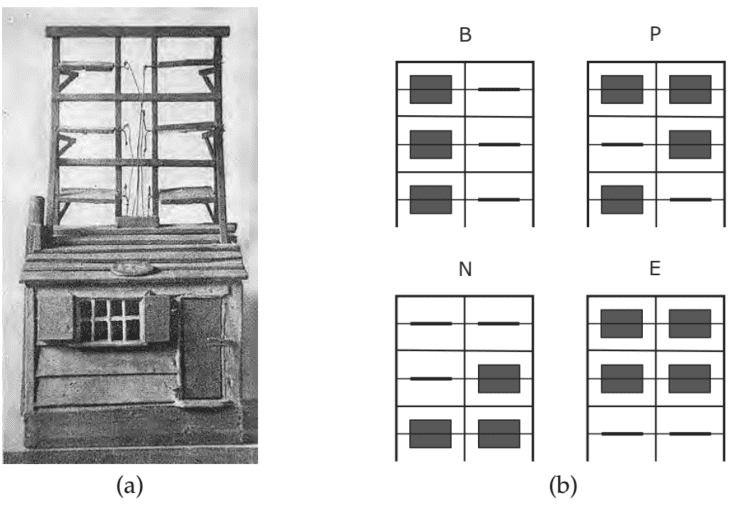
However, it wasn’t until the end of the 18th Century that a systematic approach was developed to establish telegraphic communication networks. Such networks would consist of communication posts, of which pairs would lie in each other’s line-of-sight. Typically, for these optical telegraphs, distances between two posts would be in the order of tens of kilometers, which was realistic given that high-quality telescopes could be used. An important aspect in the design of these networks was the communication protocol, which would prescribe the encoding of letters, but also what to do if there was a transmission error. To make matters more concrete, consider Figure $1.1$ which shows a model of a shutter telegraph.
数学代写|图论代写Graph Theory代考|From telephony to the Internet
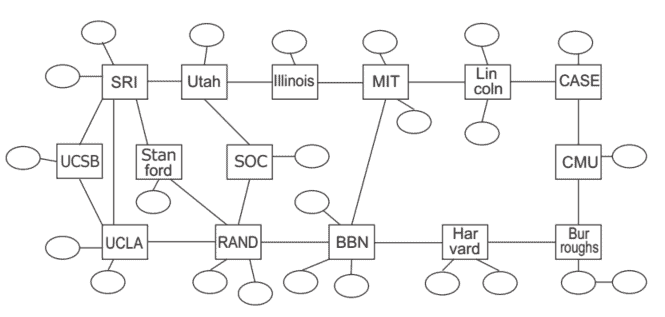
The impact of a worldwide telephony network can only be underestimated. From an end user’s perspective, it really didn’t matter anymore where you were, but only that the other party was simultaneously online. In other words, telecommunication networks realized location independency. This independency could be realized only because it was possible to establish a circuit between the two communicating parties: a communication path from one party to the other with intermediate nodes operating as switches. In most cases, these switches had fixed locations and every switch was physically linked to a few other switches. The combination of switches and links form a communication network, which can be represented mathematically by what is known as a graph, the object of study in this book.
As we already discussed, telecommunication networks were well established when people began to think about connecting computers and thus establishing data communication networks. Of course, the many existing networks already made it possible to send data, for example, as a telegram. The new challenge was to connecting these separate networks into logically a single one that could be used by computers using the same protocol. This led to the idea of building a communication system in which possibly large messages were split into smaller units called packets. Each packet would be tagged with the address of its destination and subsequently routed through the various networks. It is important to note that packets from the same message could each follow their own route to the destination, where they would then be subsequently used to reassemble the original message.
数学代写|图论代写Graph Theory代考|The Web and Wikis
Next to the importance of e-mail and other Internet messaging systems, there is little discussion about the impact of the World Wide Web. The Web is an example of a digital information space: a collection of units of information, linked together into a network. The Web is perhaps the biggest information space that we know of today: by the end of January 2005, it was estimated to have at least $11.5$ billion indexable pages [Gulli and Signorini, 2005], that is, pages that could be found and indexed by the major search engines such as Google. Three years later, different studies (using different metrics) indicate that we may be dealing with $30-50$ billion pages. In any case, we are clearly dealing with a phenomenal growth.
What makes information spaces such as the Web interesting for our studies, is that again these spaces form a network. In the case of the Web, each page may (and generally will) contain links to other pages and corresponds to a node in the network. What becomes interesting are questions such as:
- If we take the number of links pointing to a page as a measure of that page’s popularity, what can we say about the number and intensity of page popularity (i.e., what is the distribution of page popularity)?
- Does the Web also share characteristics with what are known as small world networks: is it possible to navigate to any other page through only a few links?
As we shall discuss extensively in Chapter 8, the Web indeed has its own characteristics, some of which correspond to those in small worlds. However, there are also important differences. For example, it turns out that the distribution of page popularity is very skewed: there are relatively few, but extremely popular pages. In contrast, by far most pages are not popular, yet there are many of such unpopular pages, which makes the collection of unpopular pages by itself and interesting subject for study.
图论代写
数学代写|图论代写GRAPH THEORY代考|HISTORICAL PERSPECTIVE
要拥有一个互联的世界,很明显我们需要沟通。如果我们想让这个世界有很大的覆盖范围,那么远程通信显然很重要。正如 Holzmann 和 Pehrson 所描述的,与许多人倾向于相信的不同,促进这种交流的网络有着悠久的历史1995. 除了发送信使或使用鸽子等众所周知的通信方式外,无需物理传输消息的远距离通信一直受到人类的关注。通常,这种电报通信过去是通过火标、镜子完成的一世.和.,H和l一世这Gr一种pH一世CC这米米在n一世C一种吨一世这n、 鼓和旗帜。使用这种方法建立的通信路径,例如通过在视线距离处组织通信站,在希腊和罗马历史中是已知的。
然而,直到 18 世纪末,才开发出一种系统的方法来建立电报通信网络。这样的网络将由通信站组成,其中对将位于彼此的视线范围内。通常,对于这些光学电报,两个柱子之间的距离约为数十公里,考虑到可以使用高质量的望远镜,这是现实的。这些网络设计的一个重要方面是通信协议,它规定了字母的编码,以及如果出现传输错误该怎么办。为了使事情更具体,请考虑图1.1它显示了快门电报的模型。
数学代写|图论代写GRAPH THEORY代考|FROM TELEPHONY TO THE INTERNET
全球电话网络的影响只能被低估。从最终用户的角度来看,你在哪里真的不重要了,重要的是对方同时在线。换句话说,电信网络实现了位置无关性。之所以能够实现这种独立性,是因为可以在两个通信方之间建立一条电路:从一方到另一方的通信路径,中间节点充当交换机。在大多数情况下,这些交换机都有固定的位置,并且每个交换机都与其他几个交换机物理连接。交换机和链路的组合形成了一个通信网络,它可以在数学上用所谓的图表来表示,这是本书的研究对象。
正如我们已经讨论过的,当人们开始考虑连接计算机并因此建立数据通信网络时,电信网络已经很好地建立起来。当然,许多现有的网络已经使发送数据成为可能,例如,作为电报。新的挑战是将这些独立的网络在逻辑上连接成一个可以被使用相同协议的计算机使用的单一网络。这导致了构建一个通信系统的想法,在该系统中,可能较大的消息被分成称为数据包的较小单元。每个数据包都将被标记其目的地的地址,并随后通过各种网络进行路由。重要的是要注意来自同一消息的数据包每个都可以按照自己的路线到达目的地,
数学代写|图论代写GRAPH THEORY代考|THE WEB AND WIKIS
除了电子邮件和其他 Internet 消息系统的重要性之外,很少有人讨论万维网的影响。网络是数字信息空间的一个例子:信息单元的集合,连接在一起形成一个网络。Web 可能是我们今天所知的最大的信息空间:到 2005 年 1 月末,据估计至少有11.5十亿可索引页面G在ll一世一种nd小号一世Gn这r一世n一世,2005,即可以被谷歌等主要搜索引擎找到并索引的页面。三年后,不同的研究在s一世nGd一世FF和r和n吨米和吨r一世Cs表明我们可能正在处理30−50亿页。无论如何,我们显然正在应对惊人的增长。
是什么让信息空间(如网络)对我们的研究感兴趣,因为这些空间再次形成了一个网络。在 Web 的情况下,每个页面都可以一种ndG和n和r一种ll是在一世ll包含指向其他页面的链接并对应于网络中的一个节点。变得有趣的是以下问题:
- 如果我们以指向一个页面的链接数量作为衡量该页面受欢迎程度的标准,那么我们可以说页面受欢迎程度的数量和强度如何?一世.和.,在H一种吨一世s吨H和d一世s吨r一世b在吨一世这n这Fp一种G和p这p在l一种r一世吨是?
- Web 是否也与所谓的小世界网络共享特征:是否可以通过几个链接导航到任何其他页面?
正如我们将在第 8 章中广泛讨论的那样,Web 确实有自己的特点,其中一些与小世界中的特点相对应。但是,也有重要的区别。例如,事实证明页面受欢迎程度的分布非常不平衡:页面相对较少,但非常受欢迎。相比之下,到目前为止,大多数页面并不受欢迎,但这样的冷门页面却很多,这使得冷门页面的收集本身成为一个有趣的研究课题。

数学代写|图论代写Graph Theory代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。