如果你也在 怎样代写断裂力学Fracture mechanics TMM4160这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。断裂力学Fracture mechanics是研究材料中裂纹扩展的力学领域。它使用分析性固体力学的方法来计算裂纹的驱动力,使用实验性固体力学的方法来描述材料的抗断裂性。
断裂力学Fracture mechanics从理论上讲,尖锐裂纹尖端前方的应力变得无限大,不能用来描述裂纹周围的状态。断裂力学用于表征裂纹上的载荷,通常使用一个参数来描述裂纹尖端的完整载荷状态。许多不同的参数已经被开发出来。当裂纹尖端的塑性区相对于裂纹长度较小时,裂纹尖端的应力状态是材料内部弹性力的结果,被称为线性弹性断裂力学(LEFM),可以用应力强度因子{displaystyle K}K来描述。尽管裂纹上的载荷可以是任意的,但在1957年,G. Irwin发现任何状态都可以简化为三个独立的应力强度因子的组合。
断裂力学Fracture mechanics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的断裂力学Fracture mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此断裂力学Fracture mechanics作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在物理Physical代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在断裂力学Fracture mechanics代写方面经验极为丰富,各种断裂力学Fracture mechanics相关的作业也就用不着说。
物理代写|断裂力学代写Fracture mechanics代考|Mechanical behavior under tension
The simplest way to observe the mechanical behavior of a solid is by applying a tension force on a body of regular cross-section and record the load and elongation produced in the test specimen. The typical Load versus Elongation record of an engineering material is shown in Fig. 1.4. By using the definition of stress as $\sigma=F / A_0$, where $A_0$ is the initial cross-section area of the test specimen, and defining the elongation strain as $\varepsilon=\Delta l / l_0$, where $\Delta l$ is the elongation and $l_0$ is the initial length, the stress-strain curve in tension can be reconstructed from the original Load-Elongation curve. Since $A_0$ and $l_0$ are constants, the shape of the curve does not change, only the scale is modified, therefore the stress-strain curve in uniaxial tension has the same shape of the Load-Elongation curve.
As it can be observed on the stress-strain curve, at the onset of loading, the elongation is proportional to the stress, but if the load is removed, the body recovers its initial shape and length; this behavior is termed as elastic. In most materials, the strain is linearly proportional to the strain and the constant of proportionality is called the Young’s modulus, represented by the symbol $E$. When the stress surpasses a limit value the deformation becomes permanent, a condition termed as plastic strain, the stress at this point is termed as the yield strength, and it usually represented by the symbol $\sigma_0$. On further loading, the load has to be increased to sustain the plastic deformation, this behavior is called strain hardening and it makes the curve to take a parabolic-like shape, which maximum is referred as ultimate tensile strength, represented by the symbol $\sigma_{\text {uts. }}$ Just after the ultimate tensile strength is reached, the material experiences a local contraction known as necking, so the cross-section area is rapidly reduced and the load drops, leading to the final rupture. The maximum elongation in tension loading is referred as ductility, identified by the symbol $\varepsilon_f$. These essential features of the stressstrain curve in uniaxial tension allow determining the fundamental mechanical properties of engineering materials, which are:
- Young’s modulus (E): Proportionality constant between strain and stress in the elastic regime.
- Yield strength $\left(\sigma_0\right)$ : Tension stress at the onset of plastic deformation.
- Ultimate tensile strength $\left(\sigma_{u t s}\right)$ : Maximum tension stress that a material can withstand before failure.
- Rupture elongation or ductility $\left(\varepsilon_f\right)$ : Maximum plastic elongation measured after rupture in tension.
物理代写|断裂力学代写Fracture mechanics代考|The stress tensor
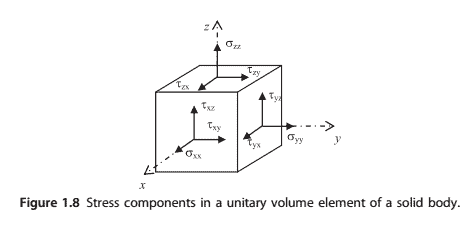
According to Cauchy’s stress theory, the state of stress at one point is described by the stress tensor which is determined by the stress components acting on the faces of an element of a differential volume (a cube) located at the origin of a Cartesian coordinate system of $x, y$, and $z$ axes, as shown in Fig. 1.8.
This results in nine stress components, three normal and six shear. An index notation identifies each stress component:
$$
\sigma_{i j}
$$
Where $i$ is the cube’s face where the stress is acting, and $j$ is the direction of the stress.
The nine stress components written in matrix form, become the stress tensor, since they are vectors, and it has the form:
$$
\boldsymbol{\sigma}=\left(\begin{array}{lll}
\sigma_{x x} & \tau_{x y} & \tau_{x z} \
\tau_{y x} & \sigma_{y y} & \tau_{y z} \
\tau_{z x} & \tau_{z y} & \sigma_{z z}
\end{array}\right)
$$
断裂力学代写
物理代写|断裂力学代写断裂力学代考|张力作用下的力学行为
观察固体的力学行为最简单的方法是在一个规则截面的物体上施加拉力,并记录试样中产生的载荷和伸长率。工程材料的典型载荷与伸长率记录如图1.4所示。将应力定义为$\sigma=F / A_0$,其中$A_0$为试件的初始横截面面积,将延伸应变定义为$\varepsilon=\Delta l / l_0$,其中$\Delta l$为伸长率,$l_0$为初始长度,可以由原来的载荷-延伸曲线重构拉伸中的应力-应变曲线。由于$A_0$和$l_0$为常数,因此曲线的形状没有改变,只是尺度被修改了,因此单轴拉伸的应力-应变曲线与load -伸长率曲线的形状相同
在应力-应变曲线上可以观察到,在加载开始时,伸长率与应力成正比,但如果去除负载,物体恢复其初始形状和长度;这种行为被称为弹性行为。在大多数材料中,应变与应变成线性正比,比例常数称为杨氏模量,用符号$E$表示。当应力超过一个限制值时,变形变为永久性的,这种情况称为塑性应变,此时的应力称为屈服强度,通常用符号$\sigma_0$表示。在进一步加载时,必须增加载荷以维持塑性变形,这种行为称为应变硬化,它使曲线呈抛物线状,其最大值称为极限抗拉强度,用符号$\sigma_{\text {uts. }}$表示,在达到极限抗拉强度后,材料发生局部收缩,称为颈缩,因此截面面积迅速减小,载荷下降,导致最终破裂。拉伸载荷中的最大伸长率称为延性,用符号$\varepsilon_f$表示。单轴拉伸中应力-应变曲线的这些基本特征决定了工程材料的基本力学性能,即
杨氏模量(E):弹性状态下应变与应力的比例常数。屈服强度$\left(\sigma_0\right)$:塑性变形开始时的拉应力。
极限拉伸强度$\left(\sigma_{u t s}\right)$:材料在失效前所能承受的最大拉伸应力。
断裂伸长率或延展性$\left(\varepsilon_f\right)$:拉伸断裂后测量的最大塑性伸长率
物理代写|断裂力学代写骨折力学代考|应力张量
根据柯西应力理论,一点的应力状态由应力张量描述,应力张量由作用于微分体(立方体)的一个单元面上的应力分量决定,该单元位于$x, y$轴和$z$轴的笛卡尔坐标系的原点,如图1.8所示这导致9个应力成分,3个正常和6个剪切。
$$
\sigma_{i j}
$$
其中$i$是应力作用的立方体的面,$j$是应力的方向。9个应力分量写成矩阵形式,成为应力张量,因为它们是矢量,它的形式是:
$$
\boldsymbol{\sigma}=\left(\begin{array}{lll}
\sigma_{x x} & \tau_{x y} & \tau_{x z} \
\tau_{y x} & \sigma_{y y} & \tau_{y z} \
\tau_{z x} & \tau_{z y} & \sigma_{z z}
\end{array}\right)
$$

物理代写|断裂力学代写Fracture mechanics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。

