如果你也在 怎样代写计算机视觉Computer Vision CS766这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。计算机视觉Computer Vision是人工智能(AI)的一个领域,使计算机和系统能够从数字图像、视频和其他视觉输入中获得有意义的信息–并根据这些信息采取行动或提出建议。如果说人工智能使计算机能够思考,那么计算机视觉则使它们能够看到、观察和理解。
计算机视觉Computer Vision任务包括获取、处理、分析和理解数字图像的方法,以及从现实世界中提取高维数据以产生数字或符号信息,例如以决策的形式。这里的理解意味着将视觉图像(视网膜的输入)转化为对思维过程有意义的世界描述,并能引起适当的行动。这种图像理解可以被看作是利用借助几何学、物理学、统计学和学习理论构建的模型将符号信息从图像数据中分离出来的过程。
计算机视觉Computer Vision代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的计算机视觉Computer Vision作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计算机视觉Computer Vision作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在计算机Quantum computer代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计算机Quantum computer代写服务。我们的专家在计算机视觉Computer Vision代写方面经验极为丰富,各种计算机视觉Computer Vision相关的作业也就用不着 说。
计算机代写|计算机视觉代写Computer Vision代考|Discrete Optimization
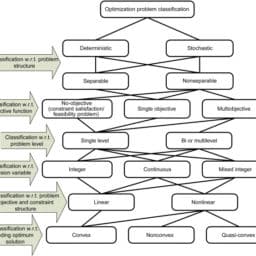
Discrete optimization deals with problems where the elements of the solution set $S$ take discrete values, e.g., $S \subseteq \mathbb{Z}^n=\left{i_1, i_2, \ldots, i_n\right} ; i_n \in \mathbb{Z}$.
Usually, discrete optimization problems are $N P$-hard to solve, which, informally speaking, in essence states that there is no known algorithm which finds the correct solution in polynomial time. Therefore, execution times soon become infeasible as the size of the problem (the number of unknowns) grows.
As a consequence, many discrete optimization methods aim at finding approximate solutions, which can often be proven to be located within some reasonable bounds to the “true” optimum. These methods are often compared in terms of the quality of the solution they provide, i.e., how close the approximate solution gets to the “true” optimal solution. This is in contrast to continuous optimization problems, which aim at optimizing their rate of convergence to local minima of the objective function.
In practice it turns out that the fact that the solution can only take discrete values, which acts as an additional constraint, often complicates matters when we efficiently want to find a solution. Therefore, a technique called relaxation can be applied, where the discrete problem is transformed into its continuous version: The objective function remains unchanged, but now the solution can take continuous values, e.g., by replacing $S_{\mathrm{d}} \subseteq \mathbb{Z}^n$ with $S_{\mathrm{c}} \subseteq \mathbb{R}^n$, i.e., the (additional) constraint that the solution has to take discrete values is dropped. The continuous representation can be solved with an appropriate continuous optimization technique. A simple way of deriving the discrete solution $x_{\mathrm{d}}^$ from the thus obtained continuous one $x_{\mathrm{c}}^$ is to choose that element of the discrete solution set $S_{\mathrm{d}}$ which is closest to $x_{\mathrm{c}}^$. Please note that there is no guarantee that $x_{\mathrm{d}}^$ is the optimal solution of the discrete problem, but under reasonable conditions it should be sufficiently close to it.
计算机代写|计算机视觉代写Computer Vision代考|Combinatorial Optimization
In combinatorial optimization, the solution set $S$ has a finite number of elements, too. Therefore, any combinatorial optimization problem is also a discrete problem. Additionally, however, for many problems it is impractical to build $S$ as an explicit enumeration of all possible solutions. Instead, a (combinatorial) solution can be expressed as a combination of some other representation of the data.
To make things clear, consider to the satnav example again. Here, $S$ is usually not represented by a simple enumeration of all possible routes from the start to a destination location. Instead, the data consists of a map of the roads, streets, motorways, etc., and each route can be obtained by combining these entities (or parts of them). Observe that this allows a much more compact representation of the solution set.
This representation leads to an obvious solution strategy for optimization problems: we “just” have to try all possible combinations and find out which one yields the minimum value of the objective function. Unfortunately, this is infeasible due to the exponential growth of the number of possible solutions when the number of elements to combine increases (a fact which is sometimes called combinatorial explosion).
An example of combinatorial optimization methods used in computer vision are the so-called graph cuts, which can, e.g., be utilized in segmentation problems: consider an image showing an object in front of some kind of background. Now we want to obtain a reasonable segmentation of the foreground object from the background. Here, the image can be represented by a graph $G=(V, E)$, where each pixel $i$ is represented by a vertex $v_i \in V$, which is connected to all of its neighbors via an edge $e_{i j} \in E$ (where pixels $i$ and $j$ are adjacent pixels; typically a 4-neighborhood is considered).
A solution $s$ of the segmentation problem which separates the object region from the background consists of a set of edges (where each of these edges connects a pixel located at the border of the object to a background pixel) and can be called a cut of the graph. In order to find the best solution, a cost $c_{i j}$ can be assigned to each edge $e_{i j}$, which can be derived from the intensity difference between pixel $i$ and $j$ : the higher the intensity difference, the higher $c_{i j}$. Hence, the solution of the problem is equal to find the cut which minimizes the overall cost along the cut. As each cut defines a combination of edges, graph cuts can be used to solve combinatorial optimization problems. This combinatorial strategy clearly is superior to enumerate all possible segmentations and seek the solution by examination of every element of the enumeration.
计算机视觉代写
计算机代写|计算机视觉代写 COMPUTER VISION代 考|DISCRETE OPTIMIZATION
通常,离散优化问题是 $N P$ – 难以解决,非正式地说,它本质上表明没有已知的算法可以在多项式时间内找到正确的解决方案。因此,随着问题的大小,执行时间 很快变得不可行thenumberofunknowns成长。
因此,许多离散优化方法旨在找到近似解,这些近似解通常可以被证明位于“真实”最优值的一些合理范围内。这些方法通常根据它们提供的解决方案的质量进行比 较,即近似解决方案与“真实”最优解决方案的接近程度。这与连续优化问题形成对比,连续优化问题旨在优化其收敛速度到目标函数的局部最小值。
在实践中,事实证明,解决方案只能采用离散值作为附加约束,当我们有效地想要找到解决方案时,这通常会使事情复杂化。因此,可以应用一种称为松弛的技 术,将离散问题转换为其连续版本:目标函数保持不变,但现在解决方案可以采用连续值,例如,通过苩换 $S_{\mathrm{d}} \subseteq \mathbb{Z}^n$ 和 $S_{\mathrm{c}} \subseteq \mathbb{R}^n$ ,即 $a d d i t i o n a l$ 解决方安必须采 用离散值的约束被删除。可以使用适当的连续优化技术来解决连续表示。一种导出离散解的简单方法 X_{|mathrm{d}}} 从
计算机代写|计算机视觉代写COMPUTER VISION代 考|COMBINATORIAL OPTIMIZATION
在组合优化中,解集 $S$ 也有有限数量的元筙。因此,任何组合优化问题也是离散问题。然而,此外,对于许多问题,构建是不切实际的 $S$ 作为所有可能解决方秪的 明确枚举。相反,一个combinatorial解决方䅁可以表示为数据的一些其他表示的组合。
为了清楚起见,请再次考虑卫星导航示例。这里,S通常不是用从起点到目的地的所有可能路线的简单枚举来表示。相反,数据由道路、街道、高速公路等的地图 组成,每条路线都可以通过组合这些实体获得orpartsofthem. 请注意,这可以更肾凑地表示解决方安集。
这种表示为优化问题带来了一种明显的解决策略:我们“只是”必须尝试所有可能的组合并找出哪个组合产生目标函数的最小值。不幸的是,这是不可行的,因为当
计算机视觉中使用的组合优化方法的一个例子是所谓的图形切割,例如,它可以用于分割问题:考虑在某种背景前显示对象的图像。现在我们想要从背景中获得对 前景对象的合理分割。在这里,图像可以用图表来表示 $G=(V, E)$, 其中每个像綘 $i$ 由一个顶点表示 $v_i \in V$ ,它通过一条边连接到它的所有邻居 $e_{i j} \in E$ wherepixels $\$ i \$ a n d \$ j$ \$areadjacentpixels; typicallya 4 – neighborhoodisconsidered.
一个解法s 将对象区域与背景分离的分割问题由一组边傢组成whereeachoftheseedgesconnectsapixellocatedattheborderoftheobjecttoabackgroundpixel 并且可以称为图的切割。为了找到最佳解决方安,成本 $c_{i j}$ 可以分配给每条边 $e_{i j}$, 这可以从像溸之间的强度差异得出 $i$ 和 $j$ : 强度差越大,越高 $c_{i j}$. 因此,问题的解决 方案等于找到使沿切割的总成本最小化的切割。由于每个割定义了边的组合,因此可以使用图割来解决组合优化问题。这种组合策略显然优于枚举所有可能的分段 并通过检查枚举的每个元塐来寻求解决方案。

计算机代写|计算机视觉代写Computer Vision代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。