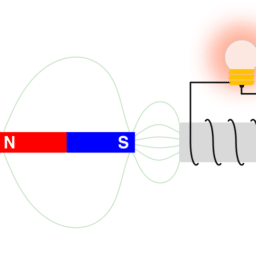
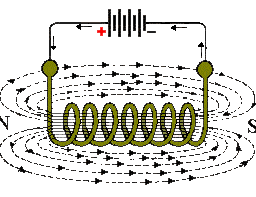
MY-ASSIGNMENTEXPERT™可以为您提供 catalog.ycp.edu PHYS350 Electromagnetism电磁学的代写代考和辅导服务!

PHYS350课程简介
This course introduces Maxwell’s equations and their applications to engineering problems. Topics covered include electrostatics, magnetostatics, magnetic fields and matter, induction, and electromagnetic waves. The reflection, transmission, and propagation of waves are studied. Applications to waveguides, transmission lines, radiation, and antennas are introduced as time permits. Prerequisite: 2.0 or higher in both ECE 270, EGR 240.
3 credit hours
Textbook
The course text will be “Introduction to Electrodynamics” by David J. Griffiths (Prentice Hall, 3rd Edition, 1998), available in the bookstore. We will cover the material in Chapters 1-7 in this course (although in a different order: see the outline below), the remaining chapters are useful for PHYS 352 Electromagnetic waves.
There are many other books on electromagnetism to look at. “Electromagnetism” by Gerald Pollock and Daniel Stump (Addison Wesley, 1st Edition, 2001) is a newer book, slightly more formal than Griffiths, and with more discussion of practical applications. Also, I recommend dipping into “Feynman Lectures Volume 2” (Addison Wesley Longman 1970), particularly for its physical insight.
Prerequisites
Instructions
The term paper will be worth 20% of the final grade. It should be about 5 pages in length on a topic related to (1) a practical everyday or technological application of electromagnetism, (2) a geo/astro/biophysical phenomenon in which electromagnetism plays a central role, (3) mathematical/numerical techniques for solving electrostatic problems, or (4) the history of electromagnetism.
You should assume that the person reading the paper has taken PHYS 350 and has a knowledge of electromagnetism at the level of the class. In your paper, you should (1) introduce the topic, and explain the background to the problem and why it is interesting, (2) carefully describe (preferably with the help of a diagram or two) the basic physics of the process, device, or experiment, and (3) perform a simple calculation (at the “back of the envelope” level) which determines the basic quantities involved, and illustrates the physics. For example, you could describe the basic physics that causes a fridge magnet to stick to the metal door, and estimate the strength of the typical magnet needed, or describe the processes involved in a lightning strike, and estimate the charge transferred, typical currents, and frequency of lightning strikes around the globe.
PHYS350 Electromagnetism HELP(EXAM HELP, ONLINE TUTOR)
Prove that Maxwell’s equations with magnetic charges and currents (as given in the first lecture) are invariant under the electric-magnetic duality transformation which rotates the electric and magnetic fields (as well as the corresponding charges and currents) into each other. That is, the equations have exactly the same form in terms of the rotated fields as the original ones. Use these steps. (a) Define rescaled fields and sources in the form
$$
\tilde{E}=\sqrt{\epsilon_0} \vec{E}, \tilde{B}=\vec{B} / \sqrt{\mu_0}, \tilde{\rho}=\rho / \sqrt{\epsilon_0}, \quad \tilde{\rho}m=\sqrt{\mu_0} \rho_m, \tilde{J}=\vec{J} / \sqrt{\epsilon_0}, \tilde{J}_m=\sqrt{\mu_0} \vec{J}_m $$ Further define the 6-component vectors $\mathcal{E} \equiv\left(\begin{array}{c}\bar{E}{\bar{B}} \ \bar{B}\end{array}\right)$ and $\mathcal{J} \equiv\left(\begin{array}{c}\bar{J} \ \bar{J}_m\end{array}\right)$, the 2-component vector $\mathcal{Q}=\left(\begin{array}{c}\bar{\rho} \ \tilde{\rho}_m\end{array}\right)$, the matrix $S \equiv\left(\begin{array}{rr}0 & -1 \ 1 & 0\end{array}\right)$ and $c=1 / \sqrt{\mu_0 \epsilon_0}$. Show that Maxwell’s equations can be expressed in the form
$$
\vec{\nabla} \times \mathcal{E}=\frac{1}{c} S\left(\mathcal{J}+\frac{\partial}{\partial t} \mathcal{E}\right), \quad \vec{\nabla} \cdot \mathcal{E}=\mathcal{Q}
$$
Notice that the $\vec{\nabla}$. and $\vec{\nabla} \times$ operations act only on the spatial indices of each 3 -vector inside the 6-vector, whereas the matrix $S$ acts the same way on each spatial component, and only rotates the $E$ and $B$ fields into each other.
To prove the invariance of Maxwell’s equations under electric-magnetic duality transformation, we need to show that the transformed fields and sources satisfy the same equations as the original ones. We define the rescaled fields and sources as given in the problem statement, and note that the transformation between electric and magnetic fields can be written as:
$$
\mathcal{E} \rightarrow S \mathcal{E}, \quad \mathcal{J} \rightarrow S \mathcal{J}, \quad \mathcal{Q} \rightarrow \mathcal{Q}
$$
where $\$ S \$$ is the matrix defined in the problem statement. This transformation preserves the form of the vector equations $\$ \backslash v e c{\backslash$ nabla} $\backslash$ cdot $\backslash \operatorname{vec}{\mathrm{E}}=\backslash \operatorname{rho} /$ /epsilon_ $0 \$$ and $\$ \backslash v e c{$ nabla $} \backslash$ times $\backslash \operatorname{vec}{B}$ $\backslash$ mu_0 \epsilon_0 $\backslash$ frac ${$ partial $\backslash$ vec ${E}} \backslash$ partial $t}=\backslash m u_{-} 0 \backslash \operatorname{vec}{J} \$$, but we need to express them in terms of the 6-component vectors $\$ \backslash$ mathcal${E} \$$ and $\$ \backslash$ mathcal${J} \$$.
Using the definition of the rescaled fields and sources, we can write:
$$
\vec{\nabla} \cdot \vec{E}=\frac{1}{\sqrt{\epsilon_0}} \vec{\nabla} \cdot \tilde{E}=\frac{1}{\sqrt{\epsilon_0}} \tilde{\rho}=\frac{1}{\sqrt{\epsilon_0}} \bar{\rho}=\mathcal{Q}1 $$ where $\$ \backslash$ mathcal${Q}{-} 1 \$$ is the first component of the 2-component vector $\$ \backslash$ mathcal${Q} \$$. This gives us the first equation in the desired form:
$$
\vec{\nabla} \cdot \mathcal{E}=\mathcal{Q}_1
$$
For the second equation, we can start with the equation for the curl of \$\vec ${\mathrm{E}} \$$ :
$$
\vec{\nabla} \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}
$$
Define rotated fields and sources $\mathcal{E}=R \mathcal{E}^{\prime}, \mathcal{Q}=R \mathcal{Q}^{\prime}$ and $\mathcal{J}=R \mathcal{J}^{\prime}$, where $R$ is the standard $2 \times 2$ rotation matrix, which acts trivially on the spatial indices of the 6-component vectors. Show that Maxwell’s equations have the same form in terms of the primed quantities. It will be useful to establish that $R$ and $S$ commute, and also that $R$ commutes with the differentiation operations (see problem 3 below). Would it still work if the rotation angle was a function of space or time?
To show that Maxwell’s equations have the same form in terms of the primed quantities, we need to show that the transformed equations take the same form as the original equations. Using the definitions of the rescaled fields and sources given in the first part of the problem, we can write the original equations as:
$$
\begin{aligned}
\nabla \cdot \vec{E} & =\frac{\rho}{\epsilon_0} \
\nabla \cdot \vec{B} & =0 \
\nabla \times \vec{E} & =-\frac{\partial \vec{B}}{\partial t} \
\nabla \times \vec{B} & =\mu_0 \vec{J}+\mu_0 \epsilon_0 \frac{\partial \vec{E}}{\partial t} \
\nabla \cdot \vec{J} & =-\frac{\partial \rho}{\partial t} \
\nabla \cdot \vec{J}_m & =-\frac{\rho_m}{\epsilon_0} \
\nabla \times \vec{J}_0 & =\epsilon_0 \mu_0 \frac{\partial \vec{J}_m}{\partial t}+\frac{\partial \vec{\rho}_m}{\partial t} \
\nabla \times \vec{J}_m & =-\frac{\partial \vec{\rho}}{\partial t}
\end{aligned}
$$
Substituting the definitions of the rescaled fields and sources and the 6 component and 2-component vectors given in the first part of the problem, we can write these equations in the form:
$$
\begin{aligned}
\nabla \cdot \tilde{E} & =\tilde{\rho} \
\nabla \cdot \tilde{B} & =0 \
\nabla \times \tilde{E} & =-\frac{1}{c} S\left(\tilde{J}+\frac{\partial}{\partial t} \tilde{E}\right) \
\nabla \times \tilde{B} & =\frac{1}{c} \tilde{J}_m+\frac{\partial}{\partial t} \tilde{E} \
\nabla \cdot \tilde{J} & =-\frac{\partial}{\partial t} \tilde{\rho} \
\nabla \cdot \tilde{J}_m & =\tilde{\rho}_m \
\nabla \times \tilde{J} & =-\frac{\partial}{\partial t} \tilde{J}_m+\frac{1}{c^2} S \frac{\partial}{\partial t}\left(\tilde{J}+\frac{\partial}{\partial t} \tilde{E}\right) \
\nabla \times \tilde{J}_m & =\frac{\partial}{\partial t} \tilde{\rho}_m
\end{aligned}
$$
We can see that these equations have the same form as the original equations, but expressed in terms of the rescaled fields and sources and the 6-component and 2-component vectors defined in the first part of the problem.
Now, we need to show that the rotated equations have the same form as the original equations. We define the rotated fields and sources as $\$ \backslash$ mathcal${E}=R \backslash$ mathcal${E}^{\wedge}{\backslash$ prime $} \$, \$ \backslash$ mathcal${Q}=R$
$\backslash$ mathcal${Q}^{\wedge}{\backslash$ prime $}$, and $\$ \backslash$ mathcal${J}=R \backslash$ mathcal ${J}^{\wedge}$

MY-ASSIGNMENTEXPERT™可以为您提供UNIVERSITY OF ILLINOIS URBANA-CHAMPAIGN MATH2940 linear algebra线性代数课程的代写代考和辅导服务! 请认准MY-ASSIGNMENTEXPERT™. MY-ASSIGNMENTEXPERT™为您的留学生涯保驾护航。